DotProduct#
- class sklearn.gaussian_process.kernels.DotProduct(sigma_0=1.0, sigma_0_bounds=(1e-05, 100000.0))[source]#
Dot-Product kernel.
The DotProduct kernel is non-stationary and can be obtained from linear regression by putting \(N(0, 1)\) priors on the coefficients of \(x_d (d = 1, . . . , D)\) and a prior of \(N(0, \sigma_0^2)\) on the bias. The DotProduct kernel is invariant to a rotation of the coordinates about the origin, but not translations. It is parameterized by a parameter sigma_0 \(\sigma\) which controls the inhomogenity of the kernel. For \(\sigma_0^2 =0\), the kernel is called the homogeneous linear kernel, otherwise it is inhomogeneous. The kernel is given by
\[k(x_i, x_j) = \sigma_0 ^ 2 + x_i \cdot x_j\]The DotProduct kernel is commonly combined with exponentiation.
See [1], Chapter 4, Section 4.2, for further details regarding the DotProduct kernel.
Read more in the User Guide.
Added in version 0.18.
- Parameters:
- sigma_0float >= 0, default=1.0
Parameter controlling the inhomogenity of the kernel. If sigma_0=0, the kernel is homogeneous.
- sigma_0_boundspair of floats >= 0 or “fixed”, default=(1e-5, 1e5)
The lower and upper bound on ‘sigma_0’. If set to “fixed”, ‘sigma_0’ cannot be changed during hyperparameter tuning.
References
Examples
>>> from sklearn.datasets import make_friedman2 >>> from sklearn.gaussian_process import GaussianProcessRegressor >>> from sklearn.gaussian_process.kernels import DotProduct, WhiteKernel >>> X, y = make_friedman2(n_samples=500, noise=0, random_state=0) >>> kernel = DotProduct() + WhiteKernel() >>> gpr = GaussianProcessRegressor(kernel=kernel, ... random_state=0).fit(X, y) >>> gpr.score(X, y) 0.3680... >>> gpr.predict(X[:2,:], return_std=True) (array([653.0..., 592.1...]), array([316.6..., 316.6...]))
- __call__(X, Y=None, eval_gradient=False)[source]#
Return the kernel k(X, Y) and optionally its gradient.
- Parameters:
- Xndarray of shape (n_samples_X, n_features)
Left argument of the returned kernel k(X, Y)
- Yndarray of shape (n_samples_Y, n_features), default=None
Right argument of the returned kernel k(X, Y). If None, k(X, X) if evaluated instead.
- eval_gradientbool, default=False
Determines whether the gradient with respect to the log of the kernel hyperparameter is computed. Only supported when Y is None.
- Returns:
- Kndarray of shape (n_samples_X, n_samples_Y)
Kernel k(X, Y)
- K_gradientndarray of shape (n_samples_X, n_samples_X, n_dims), optional
The gradient of the kernel k(X, X) with respect to the log of the hyperparameter of the kernel. Only returned when
eval_gradientis True.
- property bounds#
Returns the log-transformed bounds on the theta.
- Returns:
- boundsndarray of shape (n_dims, 2)
The log-transformed bounds on the kernel’s hyperparameters theta
- clone_with_theta(theta)[source]#
Returns a clone of self with given hyperparameters theta.
- Parameters:
- thetandarray of shape (n_dims,)
The hyperparameters
- diag(X)[source]#
Returns the diagonal of the kernel k(X, X).
The result of this method is identical to np.diag(self(X)); however, it can be evaluated more efficiently since only the diagonal is evaluated.
- Parameters:
- Xndarray of shape (n_samples_X, n_features)
Left argument of the returned kernel k(X, Y).
- Returns:
- K_diagndarray of shape (n_samples_X,)
Diagonal of kernel k(X, X).
- get_params(deep=True)[source]#
Get parameters of this kernel.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- property hyperparameters#
Returns a list of all hyperparameter specifications.
- property n_dims#
Returns the number of non-fixed hyperparameters of the kernel.
- property requires_vector_input#
Returns whether the kernel is defined on fixed-length feature vectors or generic objects. Defaults to True for backward compatibility.
- set_params(**params)[source]#
Set the parameters of this kernel.
The method works on simple kernels as well as on nested kernels. The latter have parameters of the form
<component>__<parameter>so that it’s possible to update each component of a nested object.- Returns:
- self
- property theta#
Returns the (flattened, log-transformed) non-fixed hyperparameters.
Note that theta are typically the log-transformed values of the kernel’s hyperparameters as this representation of the search space is more amenable for hyperparameter search, as hyperparameters like length-scales naturally live on a log-scale.
- Returns:
- thetandarray of shape (n_dims,)
The non-fixed, log-transformed hyperparameters of the kernel
Gallery examples#
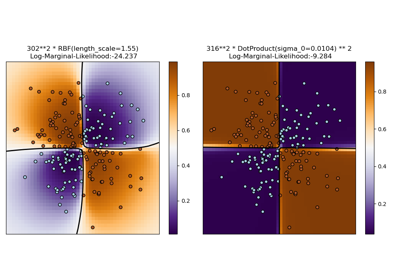
Illustration of Gaussian process classification (GPC) on the XOR dataset
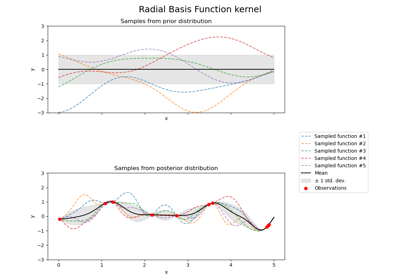
Illustration of prior and posterior Gaussian process for different kernels
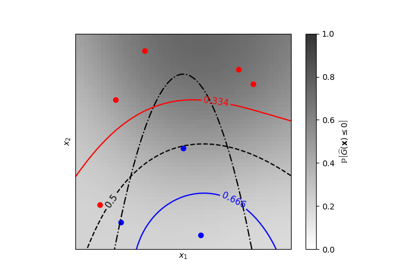
Iso-probability lines for Gaussian Processes classification (GPC)
