PolynomialFeatures#
- class sklearn.preprocessing.PolynomialFeatures(degree=2, *, interaction_only=False, include_bias=True, order='C')[source]#
Generate polynomial and interaction features.
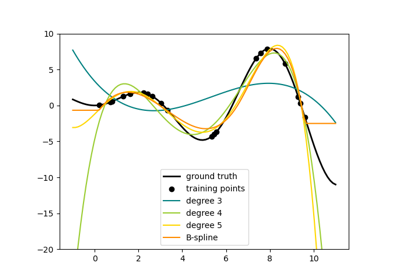
Generate a new feature matrix consisting of all polynomial combinations of the features with degree less than or equal to the specified degree. For example, if an input sample is two dimensional and of the form [a, b], the degree-2 polynomial features are [1, a, b, a^2, ab, b^2].
Read more in the User Guide.
- Parameters:
- degreeint or tuple (min_degree, max_degree), default=2
If a single int is given, it specifies the maximal degree of the polynomial features. If a tuple
(min_degree, max_degree)is passed, thenmin_degreeis the minimum andmax_degreeis the maximum polynomial degree of the generated features. Note thatmin_degree=0andmin_degree=1are equivalent as outputting the degree zero term is determined byinclude_bias.- interaction_onlybool, default=False
If
True, only interaction features are produced: features that are products of at mostdegreedistinct input features, i.e. terms with power of 2 or higher of the same input feature are excluded:included:
x[0],x[1],x[0] * x[1], etc.excluded:
x[0] ** 2,x[0] ** 2 * x[1], etc.
- include_biasbool, default=True
If
True(default), then include a bias column, the feature in which all polynomial powers are zero (i.e. a column of ones - acts as an intercept term in a linear model).- order{‘C’, ‘F’}, default=’C’
Order of output array in the dense case.
'F'order is faster to compute, but may slow down subsequent estimators.Added in version 0.21.
- Attributes:
powers_ndarray of shape (n_output_features_,n_features_in_)Exponent for each of the inputs in the output.
- n_features_in_int
Number of features seen during fit.
Added in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.Added in version 1.0.
- n_output_features_int
The total number of polynomial output features. The number of output features is computed by iterating over all suitably sized combinations of input features.
See also
SplineTransformerTransformer that generates univariate B-spline bases for features.
Notes
Be aware that the number of features in the output array scales polynomially in the number of features of the input array, and exponentially in the degree. High degrees can cause overfitting.
See examples/linear_model/plot_polynomial_interpolation.py
Examples
>>> import numpy as np >>> from sklearn.preprocessing import PolynomialFeatures >>> X = np.arange(6).reshape(3, 2) >>> X array([[0, 1], [2, 3], [4, 5]]) >>> poly = PolynomialFeatures(2) >>> poly.fit_transform(X) array([[ 1., 0., 1., 0., 0., 1.], [ 1., 2., 3., 4., 6., 9.], [ 1., 4., 5., 16., 20., 25.]]) >>> poly = PolynomialFeatures(interaction_only=True) >>> poly.fit_transform(X) array([[ 1., 0., 1., 0.], [ 1., 2., 3., 6.], [ 1., 4., 5., 20.]])
- fit(X, y=None)[source]#
Compute number of output features.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The data.
- yIgnored
Not used, present here for API consistency by convention.
- Returns:
- selfobject
Fitted transformer.
- fit_transform(X, y=None, **fit_params)[source]#
Fit to data, then transform it.
Fits transformer to
Xandywith optional parametersfit_paramsand returns a transformed version ofX.- Parameters:
- Xarray-like of shape (n_samples, n_features)
Input samples.
- yarray-like of shape (n_samples,) or (n_samples, n_outputs), default=None
Target values (None for unsupervised transformations).
- **fit_paramsdict
Additional fit parameters.
- Returns:
- X_newndarray array of shape (n_samples, n_features_new)
Transformed array.
- get_feature_names_out(input_features=None)[source]#
Get output feature names for transformation.
- Parameters:
- input_featuresarray-like of str or None, default=None
Input features.
If
input_features is None, thenfeature_names_in_is used as feature names in. Iffeature_names_in_is not defined, then the following input feature names are generated:["x0", "x1", ..., "x(n_features_in_ - 1)"].If
input_featuresis an array-like, theninput_featuresmust matchfeature_names_in_iffeature_names_in_is defined.
- Returns:
- feature_names_outndarray of str objects
Transformed feature names.
- get_metadata_routing()[source]#
Get metadata routing of this object.
Please check User Guide on how the routing mechanism works.
- Returns:
- routingMetadataRequest
A
MetadataRequestencapsulating routing information.
- get_params(deep=True)[source]#
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- property powers_#
Exponent for each of the inputs in the output.
- set_output(*, transform=None)[source]#
Set output container.
See Introducing the set_output API for an example on how to use the API.
- Parameters:
- transform{“default”, “pandas”, “polars”}, default=None
Configure output of
transformandfit_transform."default": Default output format of a transformer"pandas": DataFrame output"polars": Polars outputNone: Transform configuration is unchanged
Added in version 1.4:
"polars"option was added.
- Returns:
- selfestimator instance
Estimator instance.
- set_params(**params)[source]#
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
- transform(X)[source]#
Transform data to polynomial features.
- Parameters:
- X{array-like, sparse matrix} of shape (n_samples, n_features)
The data to transform, row by row.
Prefer CSR over CSC for sparse input (for speed), but CSC is required if the degree is 4 or higher. If the degree is less than 4 and the input format is CSC, it will be converted to CSR, have its polynomial features generated, then converted back to CSC.
If the degree is 2 or 3, the method described in “Leveraging Sparsity to Speed Up Polynomial Feature Expansions of CSR Matrices Using K-Simplex Numbers” by Andrew Nystrom and John Hughes is used, which is much faster than the method used on CSC input. For this reason, a CSC input will be converted to CSR, and the output will be converted back to CSC prior to being returned, hence the preference of CSR.
- Returns:
- XP{ndarray, sparse matrix} of shape (n_samples, NP)
The matrix of features, where
NPis the number of polynomial features generated from the combination of inputs. If a sparse matrix is provided, it will be converted into a sparsecsr_matrix.
Gallery examples#
Plot classification boundaries with different SVM Kernels