3.2. Tuning the hyper-parameters of an estimator#

Hyper-parameters are parameters that are not directly learnt within estimators. In scikit-learn they are passed as arguments to the constructor of the estimator classes. Typical examples include C, kernel and gamma for Support Vector Classifier, alpha for Lasso, etc.

It is possible and recommended to search the hyper-parameter space for the best cross validation score.

Any parameter provided when constructing an estimator may be optimized in this manner. Specifically, to find the names and current values for all parameters for a given estimator, use:

estimator.get_params()

A search consists of:

  • an estimator (regressor or classifier such as sklearn.svm.SVC());

  • a parameter space;

  • a method for searching or sampling candidates;

  • a cross-validation scheme; and

  • a score function.

Two generic approaches to parameter search are provided in scikit-learn: for given values, GridSearchCV exhaustively considers all parameter combinations, while RandomizedSearchCV can sample a given number of candidates from a parameter space with a specified distribution. Both these tools have successive halving counterparts HalvingGridSearchCV and HalvingRandomSearchCV, which can be much faster at finding a good parameter combination.

After describing these tools we detail best practices applicable to these approaches. Some models allow for specialized, efficient parameter search strategies, outlined in Alternatives to brute force parameter search.

Note that it is common that a small subset of those parameters can have a large impact on the predictive or computation performance of the model while others can be left to their default values. It is recommended to read the docstring of the estimator class to get a finer understanding of their expected behavior, possibly by reading the enclosed reference to the literature.

3.2.2. Randomized Parameter Optimization#

While using a grid of parameter settings is currently the most widely used method for parameter optimization, other search methods have more favorable properties. RandomizedSearchCV implements a randomized search over parameters, where each setting is sampled from a distribution over possible parameter values. This has two main benefits over an exhaustive search:

  • A budget can be chosen independent of the number of parameters and possible values.

  • Adding parameters that do not influence the performance does not decrease efficiency.

Specifying how parameters should be sampled is done using a dictionary, very similar to specifying parameters for GridSearchCV. Additionally, a computation budget, being the number of sampled candidates or sampling iterations, is specified using the n_iter parameter. For each parameter, either a distribution over possible values or a list of discrete choices (which will be sampled uniformly) can be specified:

{'C': scipy.stats.expon(scale=100), 'gamma': scipy.stats.expon(scale=.1),
  'kernel': ['rbf'], 'class_weight':['balanced', None]}

This example uses the scipy.stats module, which contains many useful distributions for sampling parameters, such as expon, gamma, uniform, loguniform or randint.

In principle, any function can be passed that provides a rvs (random variate sample) method to sample a value. A call to the rvs function should provide independent random samples from possible parameter values on consecutive calls.

Warning

The distributions in scipy.stats prior to version scipy 0.16 do not allow specifying a random state. Instead, they use the global numpy random state, that can be seeded via np.random.seed or set using np.random.set_state. However, beginning scikit-learn 0.18, the sklearn.model_selection module sets the random state provided by the user if scipy >= 0.16 is also available.

For continuous parameters, such as C above, it is important to specify a continuous distribution to take full advantage of the randomization. This way, increasing n_iter will always lead to a finer search.

A continuous log-uniform random variable is the continuous version of a log-spaced parameter. For example to specify the equivalent of C from above, loguniform(1, 100) can be used instead of [1, 10, 100].

Mirroring the example above in grid search, we can specify a continuous random variable that is log-uniformly distributed between 1e0 and 1e3:

from sklearn.utils.fixes import loguniform
{'C': loguniform(1e0, 1e3),
 'gamma': loguniform(1e-4, 1e-3),
 'kernel': ['rbf'],
 'class_weight':['balanced', None]}

Examples

References

  • Bergstra, J. and Bengio, Y., Random search for hyper-parameter optimization, The Journal of Machine Learning Research (2012)

3.2.3. Searching for optimal parameters with successive halving#

Scikit-learn also provides the HalvingGridSearchCV and HalvingRandomSearchCV estimators that can be used to search a parameter space using successive halving [1] [2]. Successive halving (SH) is like a tournament among candidate parameter combinations. SH is an iterative selection process where all candidates (the parameter combinations) are evaluated with a small amount of resources at the first iteration. Only some of these candidates are selected for the next iteration, which will be allocated more resources. For parameter tuning, the resource is typically the number of training samples, but it can also be an arbitrary numeric parameter such as n_estimators in a random forest.

Note

The resource increase chosen should be large enough so that a large improvement in scores is obtained when taking into account statistical significance.

As illustrated in the figure below, only a subset of candidates ‘survive’ until the last iteration. These are the candidates that have consistently ranked among the top-scoring candidates across all iterations. Each iteration is allocated an increasing amount of resources per candidate, here the number of samples.

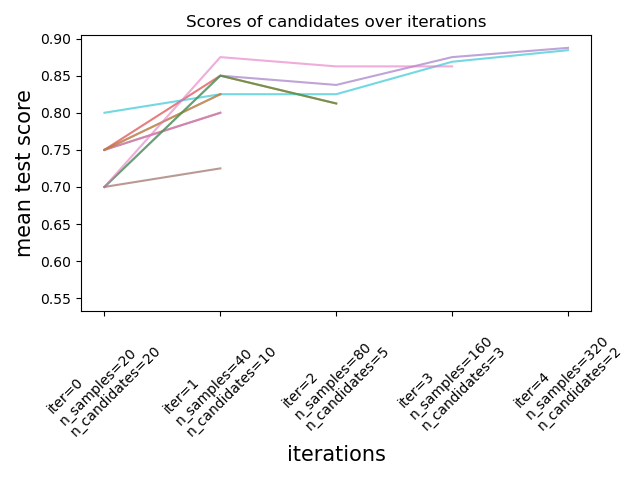
../_images/sphx_glr_plot_successive_halving_iterations_001.png

We here briefly describe the main parameters, but each parameter and their interactions are described more in detail in the dropdown section below. The factor (> 1) parameter controls the rate at which the resources grow, and the rate at which the number of candidates decreases. In each iteration, the number of resources per candidate is multiplied by factor and the number of candidates is divided by the same factor. Along with resource and min_resources, factor is the most important parameter to control the search in our implementation, though a value of 3 usually works well. factor effectively controls the number of iterations in HalvingGridSearchCV and the number of candidates (by default) and iterations in HalvingRandomSearchCV. aggressive_elimination=True can also be used if the number of available resources is small. More control is available through tuning the min_resources parameter.

These estimators are still experimental: their predictions and their API might change without any deprecation cycle. To use them, you need to explicitly import enable_halving_search_cv:

>>> from sklearn.experimental import enable_halving_search_cv  # noqa
>>> from sklearn.model_selection import HalvingGridSearchCV
>>> from sklearn.model_selection import HalvingRandomSearchCV

Examples

The sections below dive into technical aspects of successive halving.

Choosing min_resources and the number of candidates#

Beside factor, the two main parameters that influence the behaviour of a successive halving search are the min_resources parameter, and the number of candidates (or parameter combinations) that are evaluated. min_resources is the amount of resources allocated at the first iteration for each candidate. The number of candidates is specified directly in HalvingRandomSearchCV, and is determined from the param_grid parameter of HalvingGridSearchCV.

Consider a case where the resource is the number of samples, and where we have 1000 samples. In theory, with min_resources=10 and factor=2, we are able to run at most 7 iterations with the following number of samples: [10, 20, 40, 80, 160, 320, 640].

But depending on the number of candidates, we might run less than 7 iterations: if we start with a small number of candidates, the last iteration might use less than 640 samples, which means not using all the available resources (samples). For example if we start with 5 candidates, we only need 2 iterations: 5 candidates for the first iteration, then 5 // 2 = 2 candidates at the second iteration, after which we know which candidate performs the best (so we don’t need a third one). We would only be using at most 20 samples which is a waste since we have 1000 samples at our disposal. On the other hand, if we start with a high number of candidates, we might end up with a lot of candidates at the last iteration, which may not always be ideal: it means that many candidates will run with the full resources, basically reducing the procedure to standard search.

In the case of HalvingRandomSearchCV, the number of candidates is set by default such that the last iteration uses as much of the available resources as possible. For HalvingGridSearchCV, the number of candidates is determined by the param_grid parameter. Changing the value of min_resources will impact the number of possible iterations, and as a result will also have an effect on the ideal number of candidates.

Another consideration when choosing min_resources is whether or not it is easy to discriminate between good and bad candidates with a small amount of resources. For example, if you need a lot of samples to distinguish between good and bad parameters, a high min_resources is recommended. On the other hand if the distinction is clear even with a small amount of samples, then a small min_resources may be preferable since it would speed up the computation.

Notice in the example above that the last iteration does not use the maximum amount of resources available: 1000 samples are available, yet only 640 are used, at most. By default, both HalvingRandomSearchCV and HalvingGridSearchCV try to use as many resources as possible in the last iteration, with the constraint that this amount of resources must be a multiple of both min_resources and factor (this constraint will be clear in the next section). HalvingRandomSearchCV achieves this by sampling the right amount of candidates, while HalvingGridSearchCV achieves this by properly setting min_resources.

Amount of resource and number of candidates at each iteration#

At any iteration i, each candidate is allocated a given amount of resources which we denote n_resources_i. This quantity is controlled by the parameters factor and min_resources as follows (factor is strictly greater than 1):

n_resources_i = factor**i * min_resources,

or equivalently:

n_resources_{i+1} = n_resources_i * factor

where min_resources == n_resources_0 is the amount of resources used at the first iteration. factor also defines the proportions of candidates that will be selected for the next iteration:

n_candidates_i = n_candidates // (factor ** i)

or equivalently:

n_candidates_0 = n_candidates
n_candidates_{i+1} = n_candidates_i // factor

So in the first iteration, we use min_resources resources n_candidates times. In the second iteration, we use min_resources * factor resources n_candidates // factor times. The third again multiplies the resources per candidate and divides the number of candidates. This process stops when the maximum amount of resource per candidate is reached, or when we have identified the best candidate. The best candidate is identified at the iteration that is evaluating factor or less candidates (see just below for an explanation).

Here is an example with min_resources=3 and factor=2, starting with 70 candidates:

n_resources_i

n_candidates_i

3 (=min_resources)

70 (=n_candidates)

3 * 2 = 6

70 // 2 = 35

6 * 2 = 12

35 // 2 = 17

12 * 2 = 24

17 // 2 = 8

24 * 2 = 48

8 // 2 = 4

48 * 2 = 96

4 // 2 = 2

We can note that:

  • the process stops at the first iteration which evaluates factor=2 candidates: the best candidate is the best out of these 2 candidates. It is not necessary to run an additional iteration, since it would only evaluate one candidate (namely the best one, which we have already identified). For this reason, in general, we want the last iteration to run at most factor candidates. If the last iteration evaluates more than factor candidates, then this last iteration reduces to a regular search (as in RandomizedSearchCV or GridSearchCV).

  • each n_resources_i is a multiple of both factor and min_resources (which is confirmed by its definition above).

The amount of resources that is used at each iteration can be found in the n_resources_ attribute.

Choosing a resource#

By default, the resource is defined in terms of number of samples. That is, each iteration will use an increasing amount of samples to train on. You can however manually specify a parameter to use as the resource with the resource parameter. Here is an example where the resource is defined in terms of the number of estimators of a random forest:

>>> from sklearn.datasets import make_classification
>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.experimental import enable_halving_search_cv  # noqa
>>> from sklearn.model_selection import HalvingGridSearchCV
>>> import pandas as pd
>>> param_grid = {'max_depth': [3, 5, 10],
...               'min_samples_split': [2, 5, 10]}
>>> base_estimator = RandomForestClassifier(random_state=0)
>>> X, y = make_classification(n_samples=1000, random_state=0)
>>> sh = HalvingGridSearchCV(base_estimator, param_grid, cv=5,
...                          factor=2, resource='n_estimators',
...                          max_resources=30).fit(X, y)
>>> sh.best_estimator_
RandomForestClassifier(max_depth=5, n_estimators=24, random_state=0)

Note that it is not possible to budget on a parameter that is part of the parameter grid.

Exhausting the available resources#

As mentioned above, the number of resources that is used at each iteration depends on the min_resources parameter. If you have a lot of resources available but start with a low number of resources, some of them might be wasted (i.e. not used):

>>> from sklearn.datasets import make_classification
>>> from sklearn.svm import SVC
>>> from sklearn.experimental import enable_halving_search_cv  # noqa
>>> from sklearn.model_selection import HalvingGridSearchCV
>>> import pandas as pd
>>> param_grid= {'kernel': ('linear', 'rbf'),
...              'C': [1, 10, 100]}
>>> base_estimator = SVC(gamma='scale')
>>> X, y = make_classification(n_samples=1000)
>>> sh = HalvingGridSearchCV(base_estimator, param_grid, cv=5,
...                          factor=2, min_resources=20).fit(X, y)
>>> sh.n_resources_
[20, 40, 80]

The search process will only use 80 resources at most, while our maximum amount of available resources is n_samples=1000. Here, we have min_resources = r_0 = 20.

For HalvingGridSearchCV, by default, the min_resources parameter is set to ‘exhaust’. This means that min_resources is automatically set such that the last iteration can use as many resources as possible, within the max_resources limit:

>>> sh = HalvingGridSearchCV(base_estimator, param_grid, cv=5,
...                          factor=2, min_resources='exhaust').fit(X, y)
>>> sh.n_resources_
[250, 500, 1000]

min_resources was here automatically set to 250, which results in the last iteration using all the resources. The exact value that is used depends on the number of candidate parameters, on max_resources and on factor.

For HalvingRandomSearchCV, exhausting the resources can be done in 2 ways:

  • by setting min_resources='exhaust', just like for HalvingGridSearchCV;

  • by setting n_candidates='exhaust'.

Both options are mutually exclusive: using min_resources='exhaust' requires knowing the number of candidates, and symmetrically n_candidates='exhaust' requires knowing min_resources.

In general, exhausting the total number of resources leads to a better final candidate parameter, and is slightly more time-intensive.

3.2.3.1. Aggressive elimination of candidates#

Using the aggressive_elimination parameter, you can force the search process to end up with less than factor candidates at the last iteration.

Code example of aggressive elimination#

Ideally, we want the last iteration to evaluate factor candidates. We then just have to pick the best one. When the number of available resources is small with respect to the number of candidates, the last iteration may have to evaluate more than factor candidates:

>>> from sklearn.datasets import make_classification
>>> from sklearn.svm import SVC
>>> from sklearn.experimental import enable_halving_search_cv  # noqa
>>> from sklearn.model_selection import HalvingGridSearchCV
>>> import pandas as pd
>>> param_grid = {'kernel': ('linear', 'rbf'),
...               'C': [1, 10, 100]}
>>> base_estimator = SVC(gamma='scale')
>>> X, y = make_classification(n_samples=1000)
>>> sh = HalvingGridSearchCV(base_estimator, param_grid, cv=5,
...                          factor=2, max_resources=40,
...                          aggressive_elimination=False).fit(X, y)
>>> sh.n_resources_
[20, 40]
>>> sh.n_candidates_
[6, 3]

Since we cannot use more than max_resources=40 resources, the process has to stop at the second iteration which evaluates more than factor=2 candidates.

When using aggressive_elimination, the process will eliminate as many candidates as necessary using min_resources resources:

>>> sh = HalvingGridSearchCV(base_estimator, param_grid, cv=5,
...                            factor=2,
...                            max_resources=40,
...                            aggressive_elimination=True,
...                            ).fit(X, y)
>>> sh.n_resources_
[20, 20, 40]
>>> sh.n_candidates_
[6, 3, 2]

Notice that we end with 2 candidates at the last iteration since we have eliminated enough candidates during the first iterations, using n_resources = min_resources = 20.

3.2.3.2. Analyzing results with the cv_results_ attribute#

The cv_results_ attribute contains useful information for analyzing the results of a search. It can be converted to a pandas dataframe with df = pd.DataFrame(est.cv_results_). The cv_results_ attribute of HalvingGridSearchCV and HalvingRandomSearchCV is similar to that of GridSearchCV and RandomizedSearchCV, with additional information related to the successive halving process.

Example of a (truncated) output dataframe:#

iter

n_resources

mean_test_score

params

0

0

125

0.983667

{‘criterion’: ‘log_loss’, ‘max_depth’: None, ‘max_features’: 9, ‘min_samples_split’: 5}

1

0

125

0.983667

{‘criterion’: ‘gini’, ‘max_depth’: None, ‘max_features’: 8, ‘min_samples_split’: 7}

2

0

125

0.983667

{‘criterion’: ‘gini’, ‘max_depth’: None, ‘max_features’: 10, ‘min_samples_split’: 10}

3

0

125

0.983667

{‘criterion’: ‘log_loss’, ‘max_depth’: None, ‘max_features’: 6, ‘min_samples_split’: 6}

…

…

…

…

…

15

2

500

0.951958

{‘criterion’: ‘log_loss’, ‘max_depth’: None, ‘max_features’: 9, ‘min_samples_split’: 10}

16

2

500

0.947958

{‘criterion’: ‘gini’, ‘max_depth’: None, ‘max_features’: 10, ‘min_samples_split’: 10}

17

2

500

0.951958

{‘criterion’: ‘gini’, ‘max_depth’: None, ‘max_features’: 10, ‘min_samples_split’: 4}

18

3

1000

0.961009

{‘criterion’: ‘log_loss’, ‘max_depth’: None, ‘max_features’: 9, ‘min_samples_split’: 10}

19

3

1000

0.955989

{‘criterion’: ‘gini’, ‘max_depth’: None, ‘max_features’: 10, ‘min_samples_split’: 4}

Each row corresponds to a given parameter combination (a candidate) and a given iteration. The iteration is given by the iter column. The n_resources column tells you how many resources were used.

In the example above, the best parameter combination is {'criterion': 'log_loss', 'max_depth': None, 'max_features': 9, 'min_samples_split': 10} since it has reached the last iteration (3) with the highest score: 0.96.

References