Note
Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder
Label Propagation digits: Demonstrating performance#
This example demonstrates the power of semisupervised learning by training a Label Spreading model to classify handwritten digits with sets of very few labels.
The handwritten digit dataset has 1797 total points. The model will be trained using all points, but only 30 will be labeled. Results in the form of a confusion matrix and a series of metrics over each class will be very good.
At the end, the top 10 most uncertain predictions will be shown.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Data generation#
We use the digits dataset. We only use a subset of randomly selected samples.
import numpy as np
from sklearn import datasets
digits = datasets.load_digits()
rng = np.random.RandomState(2)
indices = np.arange(len(digits.data))
rng.shuffle(indices)
We selected 340 samples of which only 40 will be associated with a known label. Therefore, we store the indices of the 300 other samples for which we are not supposed to know their labels.
X = digits.data[indices[:340]]
y = digits.target[indices[:340]]
images = digits.images[indices[:340]]
n_total_samples = len(y)
n_labeled_points = 40
indices = np.arange(n_total_samples)
unlabeled_set = indices[n_labeled_points:]
Shuffle everything around
y_train = np.copy(y)
y_train[unlabeled_set] = -1
Semi-supervised learning#
We fit a LabelSpreading and use it to predict
the unknown labels.
from sklearn.metrics import classification_report
from sklearn.semi_supervised import LabelSpreading
lp_model = LabelSpreading(gamma=0.25, max_iter=20)
lp_model.fit(X, y_train)
predicted_labels = lp_model.transduction_[unlabeled_set]
true_labels = y[unlabeled_set]
print(
"Label Spreading model: %d labeled & %d unlabeled points (%d total)"
% (n_labeled_points, n_total_samples - n_labeled_points, n_total_samples)
)
Label Spreading model: 40 labeled & 300 unlabeled points (340 total)
Classification report
print(classification_report(true_labels, predicted_labels))
precision recall f1-score support
0 1.00 1.00 1.00 27
1 0.82 1.00 0.90 37
2 1.00 0.86 0.92 28
3 1.00 0.80 0.89 35
4 0.92 1.00 0.96 24
5 0.74 0.94 0.83 34
6 0.89 0.96 0.92 25
7 0.94 0.89 0.91 35
8 1.00 0.68 0.81 31
9 0.81 0.88 0.84 24
accuracy 0.90 300
macro avg 0.91 0.90 0.90 300
weighted avg 0.91 0.90 0.90 300
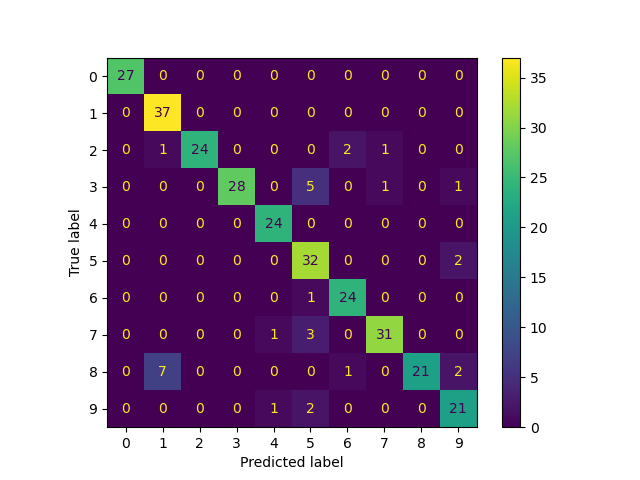
Confusion matrix
from sklearn.metrics import ConfusionMatrixDisplay
ConfusionMatrixDisplay.from_predictions(
true_labels, predicted_labels, labels=lp_model.classes_
)
<sklearn.metrics._plot.confusion_matrix.ConfusionMatrixDisplay object at 0x7faeab00db20>
Plot the most uncertain predictions#
Here, we will pick and show the 10 most uncertain predictions.
from scipy import stats
pred_entropies = stats.distributions.entropy(lp_model.label_distributions_.T)
Pick the top 10 most uncertain labels
uncertainty_index = np.argsort(pred_entropies)[-10:]
Plot
import matplotlib.pyplot as plt
f = plt.figure(figsize=(7, 5))
for index, image_index in enumerate(uncertainty_index):
image = images[image_index]
sub = f.add_subplot(2, 5, index + 1)
sub.imshow(image, cmap=plt.cm.gray_r)
plt.xticks([])
plt.yticks([])
sub.set_title(
"predict: %i\ntrue: %i" % (lp_model.transduction_[image_index], y[image_index])
)
f.suptitle("Learning with small amount of labeled data")
plt.show()

Total running time of the script: (0 minutes 0.346 seconds)
Related examples
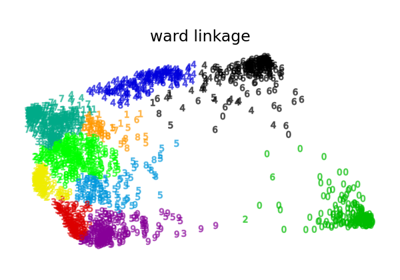
Various Agglomerative Clustering on a 2D embedding of digits