Note

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

Concatenating multiple feature extraction methods#

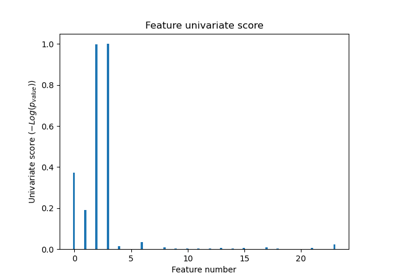
In many real-world examples, there are many ways to extract features from a dataset. Often it is beneficial to combine several methods to obtain good performance. This example shows how to use FeatureUnion to combine features obtained by PCA and univariate selection.

Combining features using this transformer has the benefit that it allows cross validation and grid searches over the whole process.

The combination used in this example is not particularly helpful on this dataset and is only used to illustrate the usage of FeatureUnion.

Combined space has 3 features
Fitting 5 folds for each of 18 candidates, totalling 90 fits
[CV 1/5; 1/18] START features__pca__n_components=1, features__univ_select__k=1, svm__C=0.1
[CV 1/5; 1/18] END features__pca__n_components=1, features__univ_select__k=1, svm__C=0.1;, score=0.933 total time=   0.0s
[CV 2/5; 1/18] START features__pca__n_components=1, features__univ_select__k=1, svm__C=0.1
[CV 2/5; 1/18] END features__pca__n_components=1, features__univ_select__k=1, svm__C=0.1;, score=0.933 total time=   0.0s
[CV 3/5; 1/18] START features__pca__n_components=1, features__univ_select__k=1, svm__C=0.1
[CV 3/5; 1/18] END features__pca__n_components=1, features__univ_select__k=1, svm__C=0.1;, score=0.867 total time=   0.0s
[CV 4/5; 1/18] START features__pca__n_components=1, features__univ_select__k=1, svm__C=0.1
[CV 4/5; 1/18] END features__pca__n_components=1, features__univ_select__k=1, svm__C=0.1;, score=0.933 total time=   0.0s
[CV 5/5; 1/18] START features__pca__n_components=1, features__univ_select__k=1, svm__C=0.1
[CV 5/5; 1/18] END features__pca__n_components=1, features__univ_select__k=1, svm__C=0.1;, score=1.000 total time=   0.0s
[CV 1/5; 2/18] START features__pca__n_components=1, features__univ_select__k=1, svm__C=1
[CV 1/5; 2/18] END features__pca__n_components=1, features__univ_select__k=1, svm__C=1;, score=0.900 total time=   0.0s
[CV 2/5; 2/18] START features__pca__n_components=1, features__univ_select__k=1, svm__C=1
[CV 2/5; 2/18] END features__pca__n_components=1, features__univ_select__k=1, svm__C=1;, score=1.000 total time=   0.0s
[CV 3/5; 2/18] START features__pca__n_components=1, features__univ_select__k=1, svm__C=1
[CV 3/5; 2/18] END features__pca__n_components=1, features__univ_select__k=1, svm__C=1;, score=0.867 total time=   0.0s
[CV 4/5; 2/18] START features__pca__n_components=1, features__univ_select__k=1, svm__C=1
[CV 4/5; 2/18] END features__pca__n_components=1, features__univ_select__k=1, svm__C=1;, score=0.933 total time=   0.0s
[CV 5/5; 2/18] START features__pca__n_components=1, features__univ_select__k=1, svm__C=1
[CV 5/5; 2/18] END features__pca__n_components=1, features__univ_select__k=1, svm__C=1;, score=1.000 total time=   0.0s
[CV 1/5; 3/18] START features__pca__n_components=1, features__univ_select__k=1, svm__C=10
[CV 1/5; 3/18] END features__pca__n_components=1, features__univ_select__k=1, svm__C=10;, score=0.933 total time=   0.0s
[CV 2/5; 3/18] START features__pca__n_components=1, features__univ_select__k=1, svm__C=10
[CV 2/5; 3/18] END features__pca__n_components=1, features__univ_select__k=1, svm__C=10;, score=1.000 total time=   0.0s
[CV 3/5; 3/18] START features__pca__n_components=1, features__univ_select__k=1, svm__C=10
[CV 3/5; 3/18] END features__pca__n_components=1, features__univ_select__k=1, svm__C=10;, score=0.900 total time=   0.0s
[CV 4/5; 3/18] START features__pca__n_components=1, features__univ_select__k=1, svm__C=10
[CV 4/5; 3/18] END features__pca__n_components=1, features__univ_select__k=1, svm__C=10;, score=0.933 total time=   0.0s
[CV 5/5; 3/18] START features__pca__n_components=1, features__univ_select__k=1, svm__C=10
[CV 5/5; 3/18] END features__pca__n_components=1, features__univ_select__k=1, svm__C=10;, score=1.000 total time=   0.0s
[CV 1/5; 4/18] START features__pca__n_components=1, features__univ_select__k=2, svm__C=0.1
[CV 1/5; 4/18] END features__pca__n_components=1, features__univ_select__k=2, svm__C=0.1;, score=0.933 total time=   0.0s
[CV 2/5; 4/18] START features__pca__n_components=1, features__univ_select__k=2, svm__C=0.1
[CV 2/5; 4/18] END features__pca__n_components=1, features__univ_select__k=2, svm__C=0.1;, score=0.967 total time=   0.0s
[CV 3/5; 4/18] START features__pca__n_components=1, features__univ_select__k=2, svm__C=0.1
[CV 3/5; 4/18] END features__pca__n_components=1, features__univ_select__k=2, svm__C=0.1;, score=0.933 total time=   0.0s
[CV 4/5; 4/18] START features__pca__n_components=1, features__univ_select__k=2, svm__C=0.1
[CV 4/5; 4/18] END features__pca__n_components=1, features__univ_select__k=2, svm__C=0.1;, score=0.933 total time=   0.0s
[CV 5/5; 4/18] START features__pca__n_components=1, features__univ_select__k=2, svm__C=0.1
[CV 5/5; 4/18] END features__pca__n_components=1, features__univ_select__k=2, svm__C=0.1;, score=1.000 total time=   0.0s
[CV 1/5; 5/18] START features__pca__n_components=1, features__univ_select__k=2, svm__C=1
[CV 1/5; 5/18] END features__pca__n_components=1, features__univ_select__k=2, svm__C=1;, score=0.933 total time=   0.0s
[CV 2/5; 5/18] START features__pca__n_components=1, features__univ_select__k=2, svm__C=1
[CV 2/5; 5/18] END features__pca__n_components=1, features__univ_select__k=2, svm__C=1;, score=0.967 total time=   0.0s
[CV 3/5; 5/18] START features__pca__n_components=1, features__univ_select__k=2, svm__C=1
[CV 3/5; 5/18] END features__pca__n_components=1, features__univ_select__k=2, svm__C=1;, score=0.933 total time=   0.0s
[CV 4/5; 5/18] START features__pca__n_components=1, features__univ_select__k=2, svm__C=1
[CV 4/5; 5/18] END features__pca__n_components=1, features__univ_select__k=2, svm__C=1;, score=0.933 total time=   0.0s
[CV 5/5; 5/18] START features__pca__n_components=1, features__univ_select__k=2, svm__C=1
[CV 5/5; 5/18] END features__pca__n_components=1, features__univ_select__k=2, svm__C=1;, score=1.000 total time=   0.0s
[CV 1/5; 6/18] START features__pca__n_components=1, features__univ_select__k=2, svm__C=10
[CV 1/5; 6/18] END features__pca__n_components=1, features__univ_select__k=2, svm__C=10;, score=0.967 total time=   0.0s
[CV 2/5; 6/18] START features__pca__n_components=1, features__univ_select__k=2, svm__C=10
[CV 2/5; 6/18] END features__pca__n_components=1, features__univ_select__k=2, svm__C=10;, score=0.967 total time=   0.0s
[CV 3/5; 6/18] START features__pca__n_components=1, features__univ_select__k=2, svm__C=10
[CV 3/5; 6/18] END features__pca__n_components=1, features__univ_select__k=2, svm__C=10;, score=0.933 total time=   0.0s
[CV 4/5; 6/18] START features__pca__n_components=1, features__univ_select__k=2, svm__C=10
[CV 4/5; 6/18] END features__pca__n_components=1, features__univ_select__k=2, svm__C=10;, score=0.933 total time=   0.0s
[CV 5/5; 6/18] START features__pca__n_components=1, features__univ_select__k=2, svm__C=10
[CV 5/5; 6/18] END features__pca__n_components=1, features__univ_select__k=2, svm__C=10;, score=1.000 total time=   0.0s
[CV 1/5; 7/18] START features__pca__n_components=2, features__univ_select__k=1, svm__C=0.1
[CV 1/5; 7/18] END features__pca__n_components=2, features__univ_select__k=1, svm__C=0.1;, score=0.933 total time=   0.0s
[CV 2/5; 7/18] START features__pca__n_components=2, features__univ_select__k=1, svm__C=0.1
[CV 2/5; 7/18] END features__pca__n_components=2, features__univ_select__k=1, svm__C=0.1;, score=1.000 total time=   0.0s
[CV 3/5; 7/18] START features__pca__n_components=2, features__univ_select__k=1, svm__C=0.1
[CV 3/5; 7/18] END features__pca__n_components=2, features__univ_select__k=1, svm__C=0.1;, score=0.867 total time=   0.0s
[CV 4/5; 7/18] START features__pca__n_components=2, features__univ_select__k=1, svm__C=0.1
[CV 4/5; 7/18] END features__pca__n_components=2, features__univ_select__k=1, svm__C=0.1;, score=0.933 total time=   0.0s
[CV 5/5; 7/18] START features__pca__n_components=2, features__univ_select__k=1, svm__C=0.1
[CV 5/5; 7/18] END features__pca__n_components=2, features__univ_select__k=1, svm__C=0.1;, score=1.000 total time=   0.0s
[CV 1/5; 8/18] START features__pca__n_components=2, features__univ_select__k=1, svm__C=1
[CV 1/5; 8/18] END features__pca__n_components=2, features__univ_select__k=1, svm__C=1;, score=0.967 total time=   0.0s
[CV 2/5; 8/18] START features__pca__n_components=2, features__univ_select__k=1, svm__C=1
[CV 2/5; 8/18] END features__pca__n_components=2, features__univ_select__k=1, svm__C=1;, score=1.000 total time=   0.0s
[CV 3/5; 8/18] START features__pca__n_components=2, features__univ_select__k=1, svm__C=1
[CV 3/5; 8/18] END features__pca__n_components=2, features__univ_select__k=1, svm__C=1;, score=0.933 total time=   0.0s
[CV 4/5; 8/18] START features__pca__n_components=2, features__univ_select__k=1, svm__C=1
[CV 4/5; 8/18] END features__pca__n_components=2, features__univ_select__k=1, svm__C=1;, score=0.933 total time=   0.0s
[CV 5/5; 8/18] START features__pca__n_components=2, features__univ_select__k=1, svm__C=1
[CV 5/5; 8/18] END features__pca__n_components=2, features__univ_select__k=1, svm__C=1;, score=1.000 total time=   0.0s
[CV 1/5; 9/18] START features__pca__n_components=2, features__univ_select__k=1, svm__C=10
[CV 1/5; 9/18] END features__pca__n_components=2, features__univ_select__k=1, svm__C=10;, score=0.967 total time=   0.0s
[CV 2/5; 9/18] START features__pca__n_components=2, features__univ_select__k=1, svm__C=10
[CV 2/5; 9/18] END features__pca__n_components=2, features__univ_select__k=1, svm__C=10;, score=0.967 total time=   0.0s
[CV 3/5; 9/18] START features__pca__n_components=2, features__univ_select__k=1, svm__C=10
[CV 3/5; 9/18] END features__pca__n_components=2, features__univ_select__k=1, svm__C=10;, score=0.900 total time=   0.0s
[CV 4/5; 9/18] START features__pca__n_components=2, features__univ_select__k=1, svm__C=10
[CV 4/5; 9/18] END features__pca__n_components=2, features__univ_select__k=1, svm__C=10;, score=0.933 total time=   0.0s
[CV 5/5; 9/18] START features__pca__n_components=2, features__univ_select__k=1, svm__C=10
[CV 5/5; 9/18] END features__pca__n_components=2, features__univ_select__k=1, svm__C=10;, score=1.000 total time=   0.0s
[CV 1/5; 10/18] START features__pca__n_components=2, features__univ_select__k=2, svm__C=0.1
[CV 1/5; 10/18] END features__pca__n_components=2, features__univ_select__k=2, svm__C=0.1;, score=0.967 total time=   0.0s
[CV 2/5; 10/18] START features__pca__n_components=2, features__univ_select__k=2, svm__C=0.1
[CV 2/5; 10/18] END features__pca__n_components=2, features__univ_select__k=2, svm__C=0.1;, score=1.000 total time=   0.0s
[CV 3/5; 10/18] START features__pca__n_components=2, features__univ_select__k=2, svm__C=0.1
[CV 3/5; 10/18] END features__pca__n_components=2, features__univ_select__k=2, svm__C=0.1;, score=0.933 total time=   0.0s
[CV 4/5; 10/18] START features__pca__n_components=2, features__univ_select__k=2, svm__C=0.1
[CV 4/5; 10/18] END features__pca__n_components=2, features__univ_select__k=2, svm__C=0.1;, score=0.933 total time=   0.0s
[CV 5/5; 10/18] START features__pca__n_components=2, features__univ_select__k=2, svm__C=0.1
[CV 5/5; 10/18] END features__pca__n_components=2, features__univ_select__k=2, svm__C=0.1;, score=1.000 total time=   0.0s
[CV 1/5; 11/18] START features__pca__n_components=2, features__univ_select__k=2, svm__C=1
[CV 1/5; 11/18] END features__pca__n_components=2, features__univ_select__k=2, svm__C=1;, score=0.967 total time=   0.0s
[CV 2/5; 11/18] START features__pca__n_components=2, features__univ_select__k=2, svm__C=1
[CV 2/5; 11/18] END features__pca__n_components=2, features__univ_select__k=2, svm__C=1;, score=1.000 total time=   0.0s
[CV 3/5; 11/18] START features__pca__n_components=2, features__univ_select__k=2, svm__C=1
[CV 3/5; 11/18] END features__pca__n_components=2, features__univ_select__k=2, svm__C=1;, score=0.933 total time=   0.0s
[CV 4/5; 11/18] START features__pca__n_components=2, features__univ_select__k=2, svm__C=1
[CV 4/5; 11/18] END features__pca__n_components=2, features__univ_select__k=2, svm__C=1;, score=0.967 total time=   0.0s
[CV 5/5; 11/18] START features__pca__n_components=2, features__univ_select__k=2, svm__C=1
[CV 5/5; 11/18] END features__pca__n_components=2, features__univ_select__k=2, svm__C=1;, score=1.000 total time=   0.0s
[CV 1/5; 12/18] START features__pca__n_components=2, features__univ_select__k=2, svm__C=10
[CV 1/5; 12/18] END features__pca__n_components=2, features__univ_select__k=2, svm__C=10;, score=0.967 total time=   0.0s
[CV 2/5; 12/18] START features__pca__n_components=2, features__univ_select__k=2, svm__C=10
[CV 2/5; 12/18] END features__pca__n_components=2, features__univ_select__k=2, svm__C=10;, score=1.000 total time=   0.0s
[CV 3/5; 12/18] START features__pca__n_components=2, features__univ_select__k=2, svm__C=10
[CV 3/5; 12/18] END features__pca__n_components=2, features__univ_select__k=2, svm__C=10;, score=0.900 total time=   0.0s
[CV 4/5; 12/18] START features__pca__n_components=2, features__univ_select__k=2, svm__C=10
[CV 4/5; 12/18] END features__pca__n_components=2, features__univ_select__k=2, svm__C=10;, score=0.933 total time=   0.0s
[CV 5/5; 12/18] START features__pca__n_components=2, features__univ_select__k=2, svm__C=10
[CV 5/5; 12/18] END features__pca__n_components=2, features__univ_select__k=2, svm__C=10;, score=1.000 total time=   0.0s
[CV 1/5; 13/18] START features__pca__n_components=3, features__univ_select__k=1, svm__C=0.1
[CV 1/5; 13/18] END features__pca__n_components=3, features__univ_select__k=1, svm__C=0.1;, score=0.967 total time=   0.0s
[CV 2/5; 13/18] START features__pca__n_components=3, features__univ_select__k=1, svm__C=0.1
[CV 2/5; 13/18] END features__pca__n_components=3, features__univ_select__k=1, svm__C=0.1;, score=1.000 total time=   0.0s
[CV 3/5; 13/18] START features__pca__n_components=3, features__univ_select__k=1, svm__C=0.1
[CV 3/5; 13/18] END features__pca__n_components=3, features__univ_select__k=1, svm__C=0.1;, score=0.933 total time=   0.0s
[CV 4/5; 13/18] START features__pca__n_components=3, features__univ_select__k=1, svm__C=0.1
[CV 4/5; 13/18] END features__pca__n_components=3, features__univ_select__k=1, svm__C=0.1;, score=0.967 total time=   0.0s
[CV 5/5; 13/18] START features__pca__n_components=3, features__univ_select__k=1, svm__C=0.1
[CV 5/5; 13/18] END features__pca__n_components=3, features__univ_select__k=1, svm__C=0.1;, score=1.000 total time=   0.0s
[CV 1/5; 14/18] START features__pca__n_components=3, features__univ_select__k=1, svm__C=1
[CV 1/5; 14/18] END features__pca__n_components=3, features__univ_select__k=1, svm__C=1;, score=0.967 total time=   0.0s
[CV 2/5; 14/18] START features__pca__n_components=3, features__univ_select__k=1, svm__C=1
[CV 2/5; 14/18] END features__pca__n_components=3, features__univ_select__k=1, svm__C=1;, score=1.000 total time=   0.0s
[CV 3/5; 14/18] START features__pca__n_components=3, features__univ_select__k=1, svm__C=1
[CV 3/5; 14/18] END features__pca__n_components=3, features__univ_select__k=1, svm__C=1;, score=0.933 total time=   0.0s
[CV 4/5; 14/18] START features__pca__n_components=3, features__univ_select__k=1, svm__C=1
[CV 4/5; 14/18] END features__pca__n_components=3, features__univ_select__k=1, svm__C=1;, score=0.967 total time=   0.0s
[CV 5/5; 14/18] START features__pca__n_components=3, features__univ_select__k=1, svm__C=1
[CV 5/5; 14/18] END features__pca__n_components=3, features__univ_select__k=1, svm__C=1;, score=1.000 total time=   0.0s
[CV 1/5; 15/18] START features__pca__n_components=3, features__univ_select__k=1, svm__C=10
[CV 1/5; 15/18] END features__pca__n_components=3, features__univ_select__k=1, svm__C=10;, score=1.000 total time=   0.0s
[CV 2/5; 15/18] START features__pca__n_components=3, features__univ_select__k=1, svm__C=10
[CV 2/5; 15/18] END features__pca__n_components=3, features__univ_select__k=1, svm__C=10;, score=1.000 total time=   0.0s
[CV 3/5; 15/18] START features__pca__n_components=3, features__univ_select__k=1, svm__C=10
[CV 3/5; 15/18] END features__pca__n_components=3, features__univ_select__k=1, svm__C=10;, score=0.933 total time=   0.0s
[CV 4/5; 15/18] START features__pca__n_components=3, features__univ_select__k=1, svm__C=10
[CV 4/5; 15/18] END features__pca__n_components=3, features__univ_select__k=1, svm__C=10;, score=0.967 total time=   0.0s
[CV 5/5; 15/18] START features__pca__n_components=3, features__univ_select__k=1, svm__C=10
[CV 5/5; 15/18] END features__pca__n_components=3, features__univ_select__k=1, svm__C=10;, score=1.000 total time=   0.0s
[CV 1/5; 16/18] START features__pca__n_components=3, features__univ_select__k=2, svm__C=0.1
[CV 1/5; 16/18] END features__pca__n_components=3, features__univ_select__k=2, svm__C=0.1;, score=0.967 total time=   0.0s
[CV 2/5; 16/18] START features__pca__n_components=3, features__univ_select__k=2, svm__C=0.1
[CV 2/5; 16/18] END features__pca__n_components=3, features__univ_select__k=2, svm__C=0.1;, score=1.000 total time=   0.0s
[CV 3/5; 16/18] START features__pca__n_components=3, features__univ_select__k=2, svm__C=0.1
[CV 3/5; 16/18] END features__pca__n_components=3, features__univ_select__k=2, svm__C=0.1;, score=0.933 total time=   0.0s
[CV 4/5; 16/18] START features__pca__n_components=3, features__univ_select__k=2, svm__C=0.1
[CV 4/5; 16/18] END features__pca__n_components=3, features__univ_select__k=2, svm__C=0.1;, score=0.967 total time=   0.0s
[CV 5/5; 16/18] START features__pca__n_components=3, features__univ_select__k=2, svm__C=0.1
[CV 5/5; 16/18] END features__pca__n_components=3, features__univ_select__k=2, svm__C=0.1;, score=1.000 total time=   0.0s
[CV 1/5; 17/18] START features__pca__n_components=3, features__univ_select__k=2, svm__C=1
[CV 1/5; 17/18] END features__pca__n_components=3, features__univ_select__k=2, svm__C=1;, score=0.967 total time=   0.0s
[CV 2/5; 17/18] START features__pca__n_components=3, features__univ_select__k=2, svm__C=1
[CV 2/5; 17/18] END features__pca__n_components=3, features__univ_select__k=2, svm__C=1;, score=1.000 total time=   0.0s
[CV 3/5; 17/18] START features__pca__n_components=3, features__univ_select__k=2, svm__C=1
[CV 3/5; 17/18] END features__pca__n_components=3, features__univ_select__k=2, svm__C=1;, score=0.967 total time=   0.0s
[CV 4/5; 17/18] START features__pca__n_components=3, features__univ_select__k=2, svm__C=1
[CV 4/5; 17/18] END features__pca__n_components=3, features__univ_select__k=2, svm__C=1;, score=0.967 total time=   0.0s
[CV 5/5; 17/18] START features__pca__n_components=3, features__univ_select__k=2, svm__C=1
[CV 5/5; 17/18] END features__pca__n_components=3, features__univ_select__k=2, svm__C=1;, score=1.000 total time=   0.0s
[CV 1/5; 18/18] START features__pca__n_components=3, features__univ_select__k=2, svm__C=10
[CV 1/5; 18/18] END features__pca__n_components=3, features__univ_select__k=2, svm__C=10;, score=1.000 total time=   0.0s
[CV 2/5; 18/18] START features__pca__n_components=3, features__univ_select__k=2, svm__C=10
[CV 2/5; 18/18] END features__pca__n_components=3, features__univ_select__k=2, svm__C=10;, score=1.000 total time=   0.0s
[CV 3/5; 18/18] START features__pca__n_components=3, features__univ_select__k=2, svm__C=10
[CV 3/5; 18/18] END features__pca__n_components=3, features__univ_select__k=2, svm__C=10;, score=0.900 total time=   0.0s
[CV 4/5; 18/18] START features__pca__n_components=3, features__univ_select__k=2, svm__C=10
[CV 4/5; 18/18] END features__pca__n_components=3, features__univ_select__k=2, svm__C=10;, score=0.967 total time=   0.0s
[CV 5/5; 18/18] START features__pca__n_components=3, features__univ_select__k=2, svm__C=10
[CV 5/5; 18/18] END features__pca__n_components=3, features__univ_select__k=2, svm__C=10;, score=1.000 total time=   0.0s
Pipeline(steps=[('features',
                 FeatureUnion(transformer_list=[('pca', PCA(n_components=3)),
                                                ('univ_select',
                                                 SelectKBest(k=1))])),
                ('svm', SVC(C=10, kernel='linear'))])

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
from sklearn.feature_selection import SelectKBest
from sklearn.model_selection import GridSearchCV
from sklearn.pipeline import FeatureUnion, Pipeline
from sklearn.svm import SVC

iris = load_iris()

X, y = iris.data, iris.target

# This dataset is way too high-dimensional. Better do PCA:
pca = PCA(n_components=2)

# Maybe some original features were good, too?
selection = SelectKBest(k=1)

# Build estimator from PCA and Univariate selection:

combined_features = FeatureUnion([("pca", pca), ("univ_select", selection)])

# Use combined features to transform dataset:
X_features = combined_features.fit(X, y).transform(X)
print("Combined space has", X_features.shape[1], "features")

svm = SVC(kernel="linear")

# Do grid search over k, n_components and C:

pipeline = Pipeline([("features", combined_features), ("svm", svm)])

param_grid = dict(
    features__pca__n_components=[1, 2, 3],
    features__univ_select__k=[1, 2],
    svm__C=[0.1, 1, 10],
)

grid_search = GridSearchCV(pipeline, param_grid=param_grid, verbose=10)
grid_search.fit(X, y)
print(grid_search.best_estimator_)