Note

Go to the end to download the full example code. or to run this example in your browser via JupyterLite or Binder

Theil-Sen Regression#

Computes a Theil-Sen Regression on a synthetic dataset.

See Theil-Sen estimator: generalized-median-based estimator for more information on the regressor.

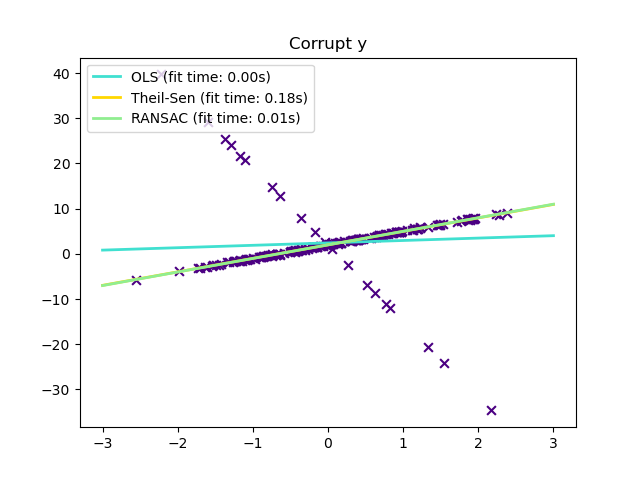
Compared to the OLS (ordinary least squares) estimator, the Theil-Sen estimator is robust against outliers. It has a breakdown point of about 29.3% in case of a simple linear regression which means that it can tolerate arbitrary corrupted data (outliers) of up to 29.3% in the two-dimensional case.

The estimation of the model is done by calculating the slopes and intercepts of a subpopulation of all possible combinations of p subsample points. If an intercept is fitted, p must be greater than or equal to n_features + 1. The final slope and intercept is then defined as the spatial median of these slopes and intercepts.

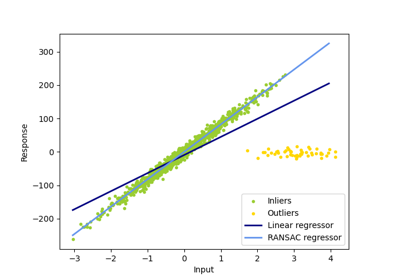
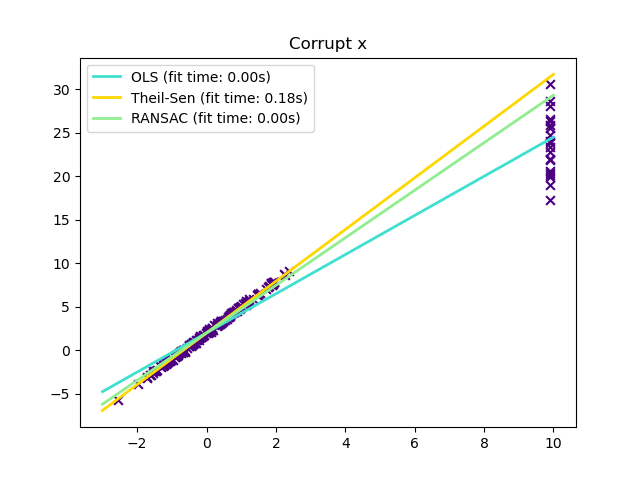
In certain cases Theil-Sen performs better than RANSAC which is also a robust method. This is illustrated in the second example below where outliers with respect to the x-axis perturb RANSAC. Tuning the residual_threshold parameter of RANSAC remedies this but in general a priori knowledge about the data and the nature of the outliers is needed. Due to the computational complexity of Theil-Sen it is recommended to use it only for small problems in terms of number of samples and features. For larger problems the max_subpopulation parameter restricts the magnitude of all possible combinations of p subsample points to a randomly chosen subset and therefore also limits the runtime. Therefore, Theil-Sen is applicable to larger problems with the drawback of losing some of its mathematical properties since it then works on a random subset.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import time

import matplotlib.pyplot as plt
import numpy as np

from sklearn.linear_model import LinearRegression, RANSACRegressor, TheilSenRegressor

estimators = [
    ("OLS", LinearRegression()),
    ("Theil-Sen", TheilSenRegressor(random_state=42)),
    ("RANSAC", RANSACRegressor(random_state=42)),
]
colors = {"OLS": "turquoise", "Theil-Sen": "gold", "RANSAC": "lightgreen"}
lw = 2

Outliers only in the y direction#

np.random.seed(0)
n_samples = 200
# Linear model y = 3*x + N(2, 0.1**2)
x = np.random.randn(n_samples)
w = 3.0
c = 2.0
noise = 0.1 * np.random.randn(n_samples)
y = w * x + c + noise
# 10% outliers
y[-20:] += -20 * x[-20:]
X = x[:, np.newaxis]

plt.scatter(x, y, color="indigo", marker="x", s=40)
line_x = np.array([-3, 3])
for name, estimator in estimators:
    t0 = time.time()
    estimator.fit(X, y)
    elapsed_time = time.time() - t0
    y_pred = estimator.predict(line_x.reshape(2, 1))
    plt.plot(
        line_x,
        y_pred,
        color=colors[name],
        linewidth=lw,
        label="%s (fit time: %.2fs)" % (name, elapsed_time),
    )

plt.axis("tight")
plt.legend(loc="upper left")
_ = plt.title("Corrupt y")

Outliers in the X direction#

np.random.seed(0)
# Linear model y = 3*x + N(2, 0.1**2)
x = np.random.randn(n_samples)
noise = 0.1 * np.random.randn(n_samples)
y = 3 * x + 2 + noise
# 10% outliers
x[-20:] = 9.9
y[-20:] += 22
X = x[:, np.newaxis]

plt.figure()
plt.scatter(x, y, color="indigo", marker="x", s=40)

line_x = np.array([-3, 10])
for name, estimator in estimators:
    t0 = time.time()
    estimator.fit(X, y)
    elapsed_time = time.time() - t0
    y_pred = estimator.predict(line_x.reshape(2, 1))
    plt.plot(
        line_x,
        y_pred,
        color=colors[name],
        linewidth=lw,
        label="%s (fit time: %.2fs)" % (name, elapsed_time),
    )

plt.axis("tight")
plt.legend(loc="upper left")
plt.title("Corrupt x")
plt.show()