Note

Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder

Compare Stochastic learning strategies for MLPClassifier¶

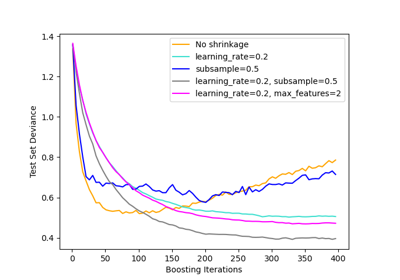
This example visualizes some training loss curves for different stochastic learning strategies, including SGD and Adam. Because of time-constraints, we use several small datasets, for which L-BFGS might be more suitable. The general trend shown in these examples seems to carry over to larger datasets, however.

Note that those results can be highly dependent on the value of learning_rate_init.

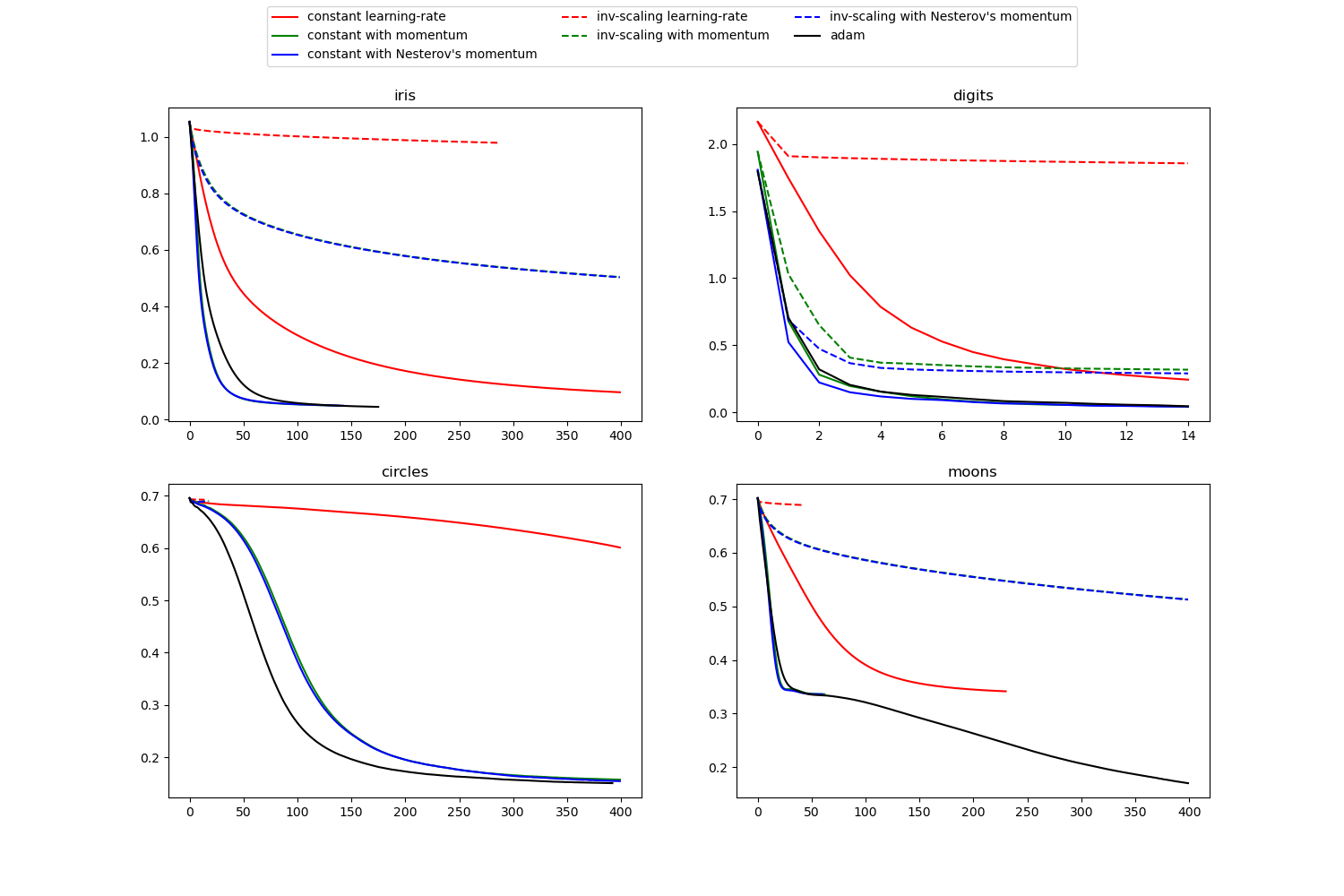
learning on dataset iris
training: constant learning-rate
Training set score: 0.980000
Training set loss: 0.096950
training: constant with momentum
Training set score: 0.980000
Training set loss: 0.049530
training: constant with Nesterov's momentum
Training set score: 0.980000
Training set loss: 0.049540
training: inv-scaling learning-rate
Training set score: 0.360000
Training set loss: 0.978444
training: inv-scaling with momentum
Training set score: 0.860000
Training set loss: 0.504185
training: inv-scaling with Nesterov's momentum
Training set score: 0.860000
Training set loss: 0.503452
training: adam
Training set score: 0.980000
Training set loss: 0.045311

learning on dataset digits
training: constant learning-rate
Training set score: 0.956038
Training set loss: 0.243802
training: constant with momentum
Training set score: 0.992766
Training set loss: 0.041297
training: constant with Nesterov's momentum
Training set score: 0.993879
Training set loss: 0.042898
training: inv-scaling learning-rate
Training set score: 0.638843
Training set loss: 1.855465
training: inv-scaling with momentum
Training set score: 0.909293
Training set loss: 0.318387
training: inv-scaling with Nesterov's momentum
Training set score: 0.912632
Training set loss: 0.290584
training: adam
Training set score: 0.991653
Training set loss: 0.045934

learning on dataset circles
training: constant learning-rate
Training set score: 0.840000
Training set loss: 0.601052
training: constant with momentum
Training set score: 0.940000
Training set loss: 0.157334
training: constant with Nesterov's momentum
Training set score: 0.940000
Training set loss: 0.154453
training: inv-scaling learning-rate
Training set score: 0.500000
Training set loss: 0.692470
training: inv-scaling with momentum
Training set score: 0.500000
Training set loss: 0.689751
training: inv-scaling with Nesterov's momentum
Training set score: 0.500000
Training set loss: 0.689143
training: adam
Training set score: 0.940000
Training set loss: 0.150527

learning on dataset moons
training: constant learning-rate
Training set score: 0.850000
Training set loss: 0.341523
training: constant with momentum
Training set score: 0.850000
Training set loss: 0.336188
training: constant with Nesterov's momentum
Training set score: 0.850000
Training set loss: 0.335919
training: inv-scaling learning-rate
Training set score: 0.500000
Training set loss: 0.689015
training: inv-scaling with momentum
Training set score: 0.830000
Training set loss: 0.513034
training: inv-scaling with Nesterov's momentum
Training set score: 0.830000
Training set loss: 0.512595
training: adam
Training set score: 0.930000
Training set loss: 0.170087

import warnings

import matplotlib.pyplot as plt

from sklearn import datasets
from sklearn.exceptions import ConvergenceWarning
from sklearn.neural_network import MLPClassifier
from sklearn.preprocessing import MinMaxScaler

# different learning rate schedules and momentum parameters
params = [
    {
        "solver": "sgd",
        "learning_rate": "constant",
        "momentum": 0,
        "learning_rate_init": 0.2,
    },
    {
        "solver": "sgd",
        "learning_rate": "constant",
        "momentum": 0.9,
        "nesterovs_momentum": False,
        "learning_rate_init": 0.2,
    },
    {
        "solver": "sgd",
        "learning_rate": "constant",
        "momentum": 0.9,
        "nesterovs_momentum": True,
        "learning_rate_init": 0.2,
    },
    {
        "solver": "sgd",
        "learning_rate": "invscaling",
        "momentum": 0,
        "learning_rate_init": 0.2,
    },
    {
        "solver": "sgd",
        "learning_rate": "invscaling",
        "momentum": 0.9,
        "nesterovs_momentum": False,
        "learning_rate_init": 0.2,
    },
    {
        "solver": "sgd",
        "learning_rate": "invscaling",
        "momentum": 0.9,
        "nesterovs_momentum": True,
        "learning_rate_init": 0.2,
    },
    {"solver": "adam", "learning_rate_init": 0.01},
]

labels = [
    "constant learning-rate",
    "constant with momentum",
    "constant with Nesterov's momentum",
    "inv-scaling learning-rate",
    "inv-scaling with momentum",
    "inv-scaling with Nesterov's momentum",
    "adam",
]

plot_args = [
    {"c": "red", "linestyle": "-"},
    {"c": "green", "linestyle": "-"},
    {"c": "blue", "linestyle": "-"},
    {"c": "red", "linestyle": "--"},
    {"c": "green", "linestyle": "--"},
    {"c": "blue", "linestyle": "--"},
    {"c": "black", "linestyle": "-"},
]


def plot_on_dataset(X, y, ax, name):
    # for each dataset, plot learning for each learning strategy
    print("\nlearning on dataset %s" % name)
    ax.set_title(name)

    X = MinMaxScaler().fit_transform(X)
    mlps = []
    if name == "digits":
        # digits is larger but converges fairly quickly
        max_iter = 15
    else:
        max_iter = 400

    for label, param in zip(labels, params):
        print("training: %s" % label)
        mlp = MLPClassifier(random_state=0, max_iter=max_iter, **param)

        # some parameter combinations will not converge as can be seen on the
        # plots so they are ignored here
        with warnings.catch_warnings():
            warnings.filterwarnings(
                "ignore", category=ConvergenceWarning, module="sklearn"
            )
            mlp.fit(X, y)

        mlps.append(mlp)
        print("Training set score: %f" % mlp.score(X, y))
        print("Training set loss: %f" % mlp.loss_)
    for mlp, label, args in zip(mlps, labels, plot_args):
        ax.plot(mlp.loss_curve_, label=label, **args)


fig, axes = plt.subplots(2, 2, figsize=(15, 10))
# load / generate some toy datasets
iris = datasets.load_iris()
X_digits, y_digits = datasets.load_digits(return_X_y=True)
data_sets = [
    (iris.data, iris.target),
    (X_digits, y_digits),
    datasets.make_circles(noise=0.2, factor=0.5, random_state=1),
    datasets.make_moons(noise=0.3, random_state=0),
]

for ax, data, name in zip(
    axes.ravel(), data_sets, ["iris", "digits", "circles", "moons"]
):
    plot_on_dataset(*data, ax=ax, name=name)

fig.legend(ax.get_lines(), labels, ncol=3, loc="upper center")
plt.show()