Note

Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder

Comparing various online solvers¶

An example showing how different online solvers perform on the hand-written digits dataset.

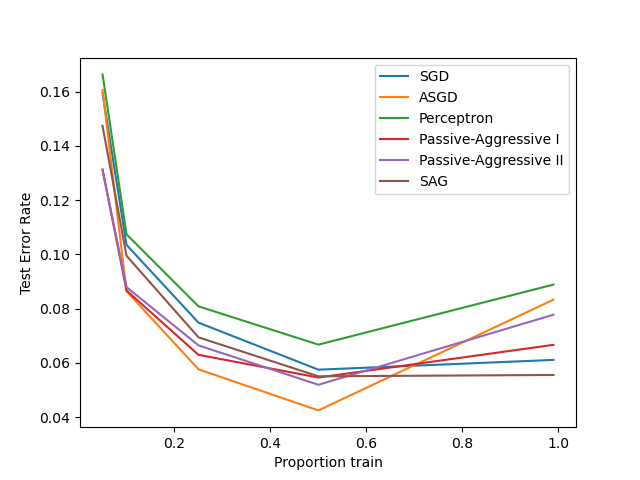
training SGD
training ASGD
training Perceptron
training Passive-Aggressive I
training Passive-Aggressive II
training SAG

# Author: Rob Zinkov <rob at zinkov dot com>
# License: BSD 3 clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn import datasets
from sklearn.linear_model import (
    LogisticRegression,
    PassiveAggressiveClassifier,
    Perceptron,
    SGDClassifier,
)
from sklearn.model_selection import train_test_split

heldout = [0.95, 0.90, 0.75, 0.50, 0.01]
# Number of rounds to fit and evaluate an estimator.
rounds = 10
X, y = datasets.load_digits(return_X_y=True)

classifiers = [
    ("SGD", SGDClassifier(max_iter=110)),
    ("ASGD", SGDClassifier(max_iter=110, average=True)),
    ("Perceptron", Perceptron(max_iter=110)),
    (
        "Passive-Aggressive I",
        PassiveAggressiveClassifier(max_iter=110, loss="hinge", C=1.0, tol=1e-4),
    ),
    (
        "Passive-Aggressive II",
        PassiveAggressiveClassifier(
            max_iter=110, loss="squared_hinge", C=1.0, tol=1e-4
        ),
    ),
    (
        "SAG",
        LogisticRegression(max_iter=110, solver="sag", tol=1e-1, C=1.0e4 / X.shape[0]),
    ),
]

xx = 1.0 - np.array(heldout)

for name, clf in classifiers:
    print("training %s" % name)
    rng = np.random.RandomState(42)
    yy = []
    for i in heldout:
        yy_ = []
        for r in range(rounds):
            X_train, X_test, y_train, y_test = train_test_split(
                X, y, test_size=i, random_state=rng
            )
            clf.fit(X_train, y_train)
            y_pred = clf.predict(X_test)
            yy_.append(1 - np.mean(y_pred == y_test))
        yy.append(np.mean(yy_))
    plt.plot(xx, yy, label=name)

plt.legend(loc="upper right")
plt.xlabel("Proportion train")
plt.ylabel("Test Error Rate")
plt.show()