Note

Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder

Train error vs Test error¶

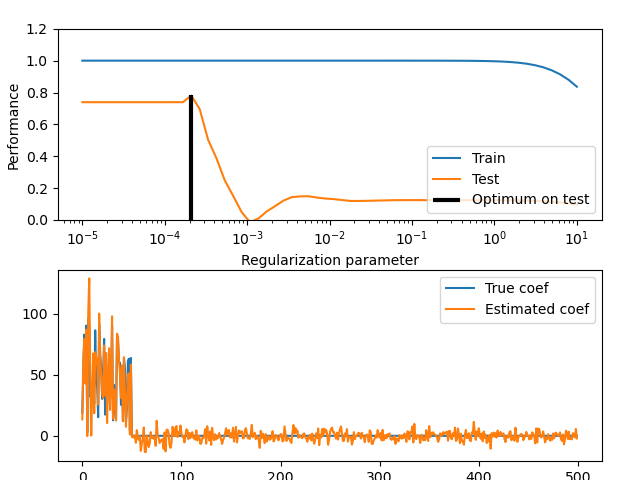
Illustration of how the performance of an estimator on unseen data (test data) is not the same as the performance on training data. As the regularization increases the performance on train decreases while the performance on test is optimal within a range of values of the regularization parameter. The example with an Elastic-Net regression model and the performance is measured using the explained variance a.k.a. R^2.

# Author: Alexandre Gramfort <alexandre.gramfort@inria.fr>
# License: BSD 3 clause

Generate sample data¶

import numpy as np

from sklearn import linear_model
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split

n_samples_train, n_samples_test, n_features = 75, 150, 500
X, y, coef = make_regression(
    n_samples=n_samples_train + n_samples_test,
    n_features=n_features,
    n_informative=50,
    shuffle=False,
    noise=1.0,
    coef=True,
)
X_train, X_test, y_train, y_test = train_test_split(
    X, y, train_size=n_samples_train, test_size=n_samples_test, shuffle=False
)

Compute train and test errors¶

alphas = np.logspace(-5, 1, 60)
enet = linear_model.ElasticNet(l1_ratio=0.7, max_iter=10000)
train_errors = list()
test_errors = list()
for alpha in alphas:
    enet.set_params(alpha=alpha)
    enet.fit(X_train, y_train)
    train_errors.append(enet.score(X_train, y_train))
    test_errors.append(enet.score(X_test, y_test))

i_alpha_optim = np.argmax(test_errors)
alpha_optim = alphas[i_alpha_optim]
print("Optimal regularization parameter : %s" % alpha_optim)

# Estimate the coef_ on full data with optimal regularization parameter
enet.set_params(alpha=alpha_optim)
coef_ = enet.fit(X, y).coef_

Optimal regularization parameter : 0.00020991037201085544

Plot results functions¶

import matplotlib.pyplot as plt

plt.subplot(2, 1, 1)
plt.semilogx(alphas, train_errors, label="Train")
plt.semilogx(alphas, test_errors, label="Test")
plt.vlines(
    alpha_optim,
    plt.ylim()[0],
    np.max(test_errors),
    color="k",
    linewidth=3,
    label="Optimum on test",
)
plt.legend(loc="lower right")
plt.ylim([0, 1.2])
plt.xlabel("Regularization parameter")
plt.ylabel("Performance")

# Show estimated coef_ vs true coef
plt.subplot(2, 1, 2)
plt.plot(coef, label="True coef")
plt.plot(coef_, label="Estimated coef")
plt.legend()
plt.subplots_adjust(0.09, 0.04, 0.94, 0.94, 0.26, 0.26)
plt.show()