6.3. Preprocessing data

The sklearn.preprocessing package provides several common utility functions and transformer classes to change raw feature vectors into a representation that is more suitable for the downstream estimators.

In general, many learning algorithms such as linear models benefit from standardization of the data set (see Importance of Feature Scaling). If some outliers are present in the set, robust scalers or other transformers can be more appropriate. The behaviors of the different scalers, transformers, and normalizers on a dataset containing marginal outliers is highlighted in Compare the effect of different scalers on data with outliers.

6.3.1. Standardization, or mean removal and variance scaling

Standardization of datasets is a common requirement for many machine learning estimators implemented in scikit-learn; they might behave badly if the individual features do not more or less look like standard normally distributed data: Gaussian with zero mean and unit variance.

In practice we often ignore the shape of the distribution and just transform the data to center it by removing the mean value of each feature, then scale it by dividing non-constant features by their standard deviation.

For instance, many elements used in the objective function of a learning algorithm (such as the RBF kernel of Support Vector Machines or the l1 and l2 regularizers of linear models) may assume that all features are centered around zero or have variance in the same order. If a feature has a variance that is orders of magnitude larger than others, it might dominate the objective function and make the estimator unable to learn from other features correctly as expected.

The preprocessing module provides the StandardScaler utility class, which is a quick and easy way to perform the following operation on an array-like dataset:

>>> from sklearn import preprocessing
>>> import numpy as np
>>> X_train = np.array([[ 1., -1.,  2.],
...                     [ 2.,  0.,  0.],
...                     [ 0.,  1., -1.]])
>>> scaler = preprocessing.StandardScaler().fit(X_train)
>>> scaler
StandardScaler()

>>> scaler.mean_
array([1. ..., 0. ..., 0.33...])

>>> scaler.scale_
array([0.81..., 0.81..., 1.24...])

>>> X_scaled = scaler.transform(X_train)
>>> X_scaled
array([[ 0.  ..., -1.22...,  1.33...],
       [ 1.22...,  0.  ..., -0.26...],
       [-1.22...,  1.22..., -1.06...]])

Scaled data has zero mean and unit variance:

>>> X_scaled.mean(axis=0)
array([0., 0., 0.])

>>> X_scaled.std(axis=0)
array([1., 1., 1.])

This class implements the Transformer API to compute the mean and standard deviation on a training set so as to be able to later re-apply the same transformation on the testing set. This class is hence suitable for use in the early steps of a Pipeline:

>>> from sklearn.datasets import make_classification
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.pipeline import make_pipeline
>>> from sklearn.preprocessing import StandardScaler

>>> X, y = make_classification(random_state=42)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
>>> pipe = make_pipeline(StandardScaler(), LogisticRegression())
>>> pipe.fit(X_train, y_train)  # apply scaling on training data
Pipeline(steps=[('standardscaler', StandardScaler()),
                ('logisticregression', LogisticRegression())])

>>> pipe.score(X_test, y_test)  # apply scaling on testing data, without leaking training data.
0.96

It is possible to disable either centering or scaling by either passing with_mean=False or with_std=False to the constructor of StandardScaler.

6.3.1.1. Scaling features to a range

An alternative standardization is scaling features to lie between a given minimum and maximum value, often between zero and one, or so that the maximum absolute value of each feature is scaled to unit size. This can be achieved using MinMaxScaler or MaxAbsScaler, respectively.

The motivation to use this scaling include robustness to very small standard deviations of features and preserving zero entries in sparse data.

Here is an example to scale a toy data matrix to the [0, 1] range:

>>> X_train = np.array([[ 1., -1.,  2.],
...                     [ 2.,  0.,  0.],
...                     [ 0.,  1., -1.]])
...
>>> min_max_scaler = preprocessing.MinMaxScaler()
>>> X_train_minmax = min_max_scaler.fit_transform(X_train)
>>> X_train_minmax
array([[0.5       , 0.        , 1.        ],
       [1.        , 0.5       , 0.33333333],
       [0.        , 1.        , 0.        ]])

The same instance of the transformer can then be applied to some new test data unseen during the fit call: the same scaling and shifting operations will be applied to be consistent with the transformation performed on the train data:

>>> X_test = np.array([[-3., -1.,  4.]])
>>> X_test_minmax = min_max_scaler.transform(X_test)
>>> X_test_minmax
array([[-1.5       ,  0.        ,  1.66666667]])

It is possible to introspect the scaler attributes to find about the exact nature of the transformation learned on the training data:

>>> min_max_scaler.scale_
array([0.5       , 0.5       , 0.33...])

>>> min_max_scaler.min_
array([0.        , 0.5       , 0.33...])

If MinMaxScaler is given an explicit feature_range=(min, max) the full formula is:

X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))

X_scaled = X_std * (max - min) + min

MaxAbsScaler works in a very similar fashion, but scales in a way that the training data lies within the range [-1, 1] by dividing through the largest maximum value in each feature. It is meant for data that is already centered at zero or sparse data.

Here is how to use the toy data from the previous example with this scaler:

>>> X_train = np.array([[ 1., -1.,  2.],
...                     [ 2.,  0.,  0.],
...                     [ 0.,  1., -1.]])
...
>>> max_abs_scaler = preprocessing.MaxAbsScaler()
>>> X_train_maxabs = max_abs_scaler.fit_transform(X_train)
>>> X_train_maxabs
array([[ 0.5, -1. ,  1. ],
       [ 1. ,  0. ,  0. ],
       [ 0. ,  1. , -0.5]])
>>> X_test = np.array([[ -3., -1.,  4.]])
>>> X_test_maxabs = max_abs_scaler.transform(X_test)
>>> X_test_maxabs
array([[-1.5, -1. ,  2. ]])
>>> max_abs_scaler.scale_
array([2.,  1.,  2.])

6.3.1.2. Scaling sparse data

Centering sparse data would destroy the sparseness structure in the data, and thus rarely is a sensible thing to do. However, it can make sense to scale sparse inputs, especially if features are on different scales.

MaxAbsScaler was specifically designed for scaling sparse data, and is the recommended way to go about this. However, StandardScaler can accept scipy.sparse matrices as input, as long as with_mean=False is explicitly passed to the constructor. Otherwise a ValueError will be raised as silently centering would break the sparsity and would often crash the execution by allocating excessive amounts of memory unintentionally. RobustScaler cannot be fitted to sparse inputs, but you can use the transform method on sparse inputs.

Note that the scalers accept both Compressed Sparse Rows and Compressed Sparse Columns format (see scipy.sparse.csr_matrix and scipy.sparse.csc_matrix). Any other sparse input will be converted to the Compressed Sparse Rows representation. To avoid unnecessary memory copies, it is recommended to choose the CSR or CSC representation upstream.

Finally, if the centered data is expected to be small enough, explicitly converting the input to an array using the toarray method of sparse matrices is another option.

6.3.1.3. Scaling data with outliers

If your data contains many outliers, scaling using the mean and variance of the data is likely to not work very well. In these cases, you can use RobustScaler as a drop-in replacement instead. It uses more robust estimates for the center and range of your data.

References:

Further discussion on the importance of centering and scaling data is available on this FAQ: Should I normalize/standardize/rescale the data?

Scaling vs Whitening

It is sometimes not enough to center and scale the features independently, since a downstream model can further make some assumption on the linear independence of the features.

To address this issue you can use PCA with whiten=True to further remove the linear correlation across features.

6.3.1.4. Centering kernel matrices

If you have a kernel matrix of a kernel \(K\) that computes a dot product in a feature space (possibly implicitly) defined by a function \(\phi(\cdot)\), a KernelCenterer can transform the kernel matrix so that it contains inner products in the feature space defined by \(\phi\) followed by the removal of the mean in that space. In other words, KernelCenterer computes the centered Gram matrix associated to a positive semidefinite kernel \(K\).

Mathematical formulation

We can have a look at the mathematical formulation now that we have the intuition. Let \(K\) be a kernel matrix of shape (n_samples, n_samples) computed from \(X\), a data matrix of shape (n_samples, n_features), during the fit step. \(K\) is defined by

\[K(X, X) = \phi(X) . \phi(X)^{T}\]

\(\phi(X)\) is a function mapping of \(X\) to a Hilbert space. A centered kernel \(\tilde{K}\) is defined as:

\[\tilde{K}(X, X) = \tilde{\phi}(X) . \tilde{\phi}(X)^{T}\]

where \(\tilde{\phi}(X)\) results from centering \(\phi(X)\) in the Hilbert space.

Thus, one could compute \(\tilde{K}\) by mapping \(X\) using the function \(\phi(\cdot)\) and center the data in this new space. However, kernels are often used because they allows some algebra calculations that avoid computing explicitly this mapping using \(\phi(\cdot)\). Indeed, one can implicitly center as shown in Appendix B in [Scholkopf1998]:

\[\tilde{K} = K - 1_{\text{n}_{samples}} K - K 1_{\text{n}_{samples}} + 1_{\text{n}_{samples}} K 1_{\text{n}_{samples}}\]

\(1_{\text{n}_{samples}}\) is a matrix of (n_samples, n_samples) where all entries are equal to \(\frac{1}{\text{n}_{samples}}\). In the transform step, the kernel becomes \(K_{test}(X, Y)\) defined as:

\[K_{test}(X, Y) = \phi(Y) . \phi(X)^{T}\]

\(Y\) is the test dataset of shape (n_samples_test, n_features) and thus \(K_{test}\) is of shape (n_samples_test, n_samples). In this case, centering \(K_{test}\) is done as:

\[\tilde{K}_{test}(X, Y) = K_{test} - 1'_{\text{n}_{samples}} K - K_{test} 1_{\text{n}_{samples}} + 1'_{\text{n}_{samples}} K 1_{\text{n}_{samples}}\]

\(1'_{\text{n}_{samples}}\) is a matrix of shape (n_samples_test, n_samples) where all entries are equal to \(\frac{1}{\text{n}_{samples}}\).

References

[Scholkopf1998]

B. Schölkopf, A. Smola, and K.R. Müller, “Nonlinear component analysis as a kernel eigenvalue problem.” Neural computation 10.5 (1998): 1299-1319.

6.3.2. Non-linear transformation

Two types of transformations are available: quantile transforms and power transforms. Both quantile and power transforms are based on monotonic transformations of the features and thus preserve the rank of the values along each feature.

Quantile transforms put all features into the same desired distribution based on the formula \(G^{-1}(F(X))\) where \(F\) is the cumulative distribution function of the feature and \(G^{-1}\) the quantile function of the desired output distribution \(G\). This formula is using the two following facts: (i) if \(X\) is a random variable with a continuous cumulative distribution function \(F\) then \(F(X)\) is uniformly distributed on \([0,1]\); (ii) if \(U\) is a random variable with uniform distribution on \([0,1]\) then \(G^{-1}(U)\) has distribution \(G\). By performing a rank transformation, a quantile transform smooths out unusual distributions and is less influenced by outliers than scaling methods. It does, however, distort correlations and distances within and across features.

Power transforms are a family of parametric transformations that aim to map data from any distribution to as close to a Gaussian distribution.

6.3.2.1. Mapping to a Uniform distribution

QuantileTransformer provides a non-parametric transformation to map the data to a uniform distribution with values between 0 and 1:

>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import train_test_split
>>> X, y = load_iris(return_X_y=True)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
>>> quantile_transformer = preprocessing.QuantileTransformer(random_state=0)
>>> X_train_trans = quantile_transformer.fit_transform(X_train)
>>> X_test_trans = quantile_transformer.transform(X_test)
>>> np.percentile(X_train[:, 0], [0, 25, 50, 75, 100]) 
array([ 4.3,  5.1,  5.8,  6.5,  7.9])

This feature corresponds to the sepal length in cm. Once the quantile transformation applied, those landmarks approach closely the percentiles previously defined:

>>> np.percentile(X_train_trans[:, 0], [0, 25, 50, 75, 100])
... 
array([ 0.00... ,  0.24...,  0.49...,  0.73...,  0.99... ])

This can be confirmed on a independent testing set with similar remarks:

>>> np.percentile(X_test[:, 0], [0, 25, 50, 75, 100])
... 
array([ 4.4  ,  5.125,  5.75 ,  6.175,  7.3  ])
>>> np.percentile(X_test_trans[:, 0], [0, 25, 50, 75, 100])
... 
array([ 0.01...,  0.25...,  0.46...,  0.60... ,  0.94...])

6.3.2.2. Mapping to a Gaussian distribution

In many modeling scenarios, normality of the features in a dataset is desirable. Power transforms are a family of parametric, monotonic transformations that aim to map data from any distribution to as close to a Gaussian distribution as possible in order to stabilize variance and minimize skewness.

PowerTransformer currently provides two such power transformations, the Yeo-Johnson transform and the Box-Cox transform.

The Yeo-Johnson transform is given by:

\[\begin{split}x_i^{(\lambda)} = \begin{cases} [(x_i + 1)^\lambda - 1] / \lambda & \text{if } \lambda \neq 0, x_i \geq 0, \\[8pt] \ln{(x_i + 1)} & \text{if } \lambda = 0, x_i \geq 0 \\[8pt] -[(-x_i + 1)^{2 - \lambda} - 1] / (2 - \lambda) & \text{if } \lambda \neq 2, x_i < 0, \\[8pt] - \ln (- x_i + 1) & \text{if } \lambda = 2, x_i < 0 \end{cases}\end{split}\]

while the Box-Cox transform is given by:

\[\begin{split}x_i^{(\lambda)} = \begin{cases} \dfrac{x_i^\lambda - 1}{\lambda} & \text{if } \lambda \neq 0, \\[8pt] \ln{(x_i)} & \text{if } \lambda = 0, \end{cases}\end{split}\]

Box-Cox can only be applied to strictly positive data. In both methods, the transformation is parameterized by \(\lambda\), which is determined through maximum likelihood estimation. Here is an example of using Box-Cox to map samples drawn from a lognormal distribution to a normal distribution:

>>> pt = preprocessing.PowerTransformer(method='box-cox', standardize=False)
>>> X_lognormal = np.random.RandomState(616).lognormal(size=(3, 3))
>>> X_lognormal
array([[1.28..., 1.18..., 0.84...],
       [0.94..., 1.60..., 0.38...],
       [1.35..., 0.21..., 1.09...]])
>>> pt.fit_transform(X_lognormal)
array([[ 0.49...,  0.17..., -0.15...],
       [-0.05...,  0.58..., -0.57...],
       [ 0.69..., -0.84...,  0.10...]])

While the above example sets the standardize option to False, PowerTransformer will apply zero-mean, unit-variance normalization to the transformed output by default.

Below are examples of Box-Cox and Yeo-Johnson applied to various probability distributions. Note that when applied to certain distributions, the power transforms achieve very Gaussian-like results, but with others, they are ineffective. This highlights the importance of visualizing the data before and after transformation.

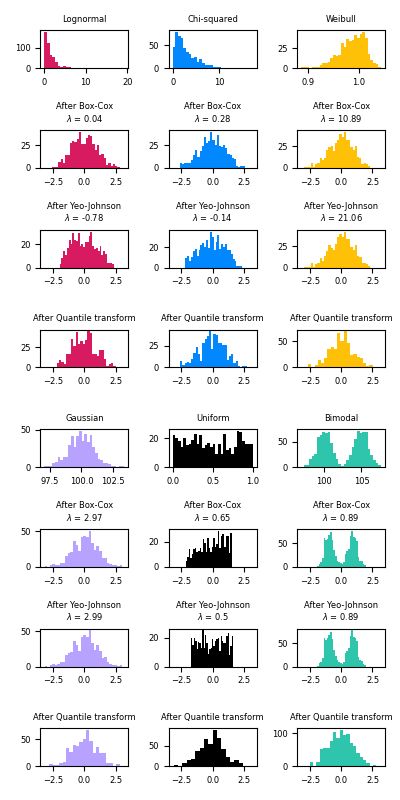
It is also possible to map data to a normal distribution using QuantileTransformer by setting output_distribution='normal'. Using the earlier example with the iris dataset:

>>> quantile_transformer = preprocessing.QuantileTransformer(
...     output_distribution='normal', random_state=0)
>>> X_trans = quantile_transformer.fit_transform(X)
>>> quantile_transformer.quantiles_
array([[4.3, 2. , 1. , 0.1],
       [4.4, 2.2, 1.1, 0.1],
       [4.4, 2.2, 1.2, 0.1],
       ...,
       [7.7, 4.1, 6.7, 2.5],
       [7.7, 4.2, 6.7, 2.5],
       [7.9, 4.4, 6.9, 2.5]])

Thus the median of the input becomes the mean of the output, centered at 0. The normal output is clipped so that the input’s minimum and maximum — corresponding to the 1e-7 and 1 - 1e-7 quantiles respectively — do not become infinite under the transformation.

6.3.3. Normalization

Normalization is the process of scaling individual samples to have unit norm. This process can be useful if you plan to use a quadratic form such as the dot-product or any other kernel to quantify the similarity of any pair of samples.

This assumption is the base of the Vector Space Model often used in text classification and clustering contexts.

The function normalize provides a quick and easy way to perform this operation on a single array-like dataset, either using the l1, l2, or max norms:

>>> X = [[ 1., -1.,  2.],
...      [ 2.,  0.,  0.],
...      [ 0.,  1., -1.]]
>>> X_normalized = preprocessing.normalize(X, norm='l2')

>>> X_normalized
array([[ 0.40..., -0.40...,  0.81...],
       [ 1.  ...,  0.  ...,  0.  ...],
       [ 0.  ...,  0.70..., -0.70...]])

The preprocessing module further provides a utility class Normalizer that implements the same operation using the Transformer API (even though the fit method is useless in this case: the class is stateless as this operation treats samples independently).

This class is hence suitable for use in the early steps of a Pipeline:

>>> normalizer = preprocessing.Normalizer().fit(X)  # fit does nothing
>>> normalizer
Normalizer()

The normalizer instance can then be used on sample vectors as any transformer:

>>> normalizer.transform(X)
array([[ 0.40..., -0.40...,  0.81...],
       [ 1.  ...,  0.  ...,  0.  ...],
       [ 0.  ...,  0.70..., -0.70...]])

>>> normalizer.transform([[-1.,  1., 0.]])
array([[-0.70...,  0.70...,  0.  ...]])

Note: L2 normalization is also known as spatial sign preprocessing.

Sparse input

normalize and Normalizer accept both dense array-like and sparse matrices from scipy.sparse as input.

For sparse input the data is converted to the Compressed Sparse Rows representation (see scipy.sparse.csr_matrix) before being fed to efficient Cython routines. To avoid unnecessary memory copies, it is recommended to choose the CSR representation upstream.

6.3.4. Encoding categorical features

Often features are not given as continuous values but categorical. For example a person could have features ["male", "female"], ["from Europe", "from US", "from Asia"], ["uses Firefox", "uses Chrome", "uses Safari", "uses Internet Explorer"]. Such features can be efficiently coded as integers, for instance ["male", "from US", "uses Internet Explorer"] could be expressed as [0, 1, 3] while ["female", "from Asia", "uses Chrome"] would be [1, 2, 1].

To convert categorical features to such integer codes, we can use the OrdinalEncoder. This estimator transforms each categorical feature to one new feature of integers (0 to n_categories - 1):

>>> enc = preprocessing.OrdinalEncoder()
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OrdinalEncoder()
>>> enc.transform([['female', 'from US', 'uses Safari']])
array([[0., 1., 1.]])

Such integer representation can, however, not be used directly with all scikit-learn estimators, as these expect continuous input, and would interpret the categories as being ordered, which is often not desired (i.e. the set of browsers was ordered arbitrarily).

By default, OrdinalEncoder will also passthrough missing values that are indicated by np.nan.

>>> enc = preprocessing.OrdinalEncoder()
>>> X = [['male'], ['female'], [np.nan], ['female']]
>>> enc.fit_transform(X)
array([[ 1.],
       [ 0.],
       [nan],
       [ 0.]])

OrdinalEncoder provides a parameter encoded_missing_value to encode the missing values without the need to create a pipeline and using SimpleImputer.

>>> enc = preprocessing.OrdinalEncoder(encoded_missing_value=-1)
>>> X = [['male'], ['female'], [np.nan], ['female']]
>>> enc.fit_transform(X)
array([[ 1.],
       [ 0.],
       [-1.],
       [ 0.]])

The above processing is equivalent to the following pipeline:

>>> from sklearn.pipeline import Pipeline
>>> from sklearn.impute import SimpleImputer
>>> enc = Pipeline(steps=[
...     ("encoder", preprocessing.OrdinalEncoder()),
...     ("imputer", SimpleImputer(strategy="constant", fill_value=-1)),
... ])
>>> enc.fit_transform(X)
array([[ 1.],
       [ 0.],
       [-1.],
       [ 0.]])

Another possibility to convert categorical features to features that can be used with scikit-learn estimators is to use a one-of-K, also known as one-hot or dummy encoding. This type of encoding can be obtained with the OneHotEncoder, which transforms each categorical feature with n_categories possible values into n_categories binary features, with one of them 1, and all others 0.

Continuing the example above:

>>> enc = preprocessing.OneHotEncoder()
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OneHotEncoder()
>>> enc.transform([['female', 'from US', 'uses Safari'],
...                ['male', 'from Europe', 'uses Safari']]).toarray()
array([[1., 0., 0., 1., 0., 1.],
       [0., 1., 1., 0., 0., 1.]])

By default, the values each feature can take is inferred automatically from the dataset and can be found in the categories_ attribute:

>>> enc.categories_
[array(['female', 'male'], dtype=object), array(['from Europe', 'from US'], dtype=object), array(['uses Firefox', 'uses Safari'], dtype=object)]

It is possible to specify this explicitly using the parameter categories. There are two genders, four possible continents and four web browsers in our dataset:

>>> genders = ['female', 'male']
>>> locations = ['from Africa', 'from Asia', 'from Europe', 'from US']
>>> browsers = ['uses Chrome', 'uses Firefox', 'uses IE', 'uses Safari']
>>> enc = preprocessing.OneHotEncoder(categories=[genders, locations, browsers])
>>> # Note that for there are missing categorical values for the 2nd and 3rd
>>> # feature
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OneHotEncoder(categories=[['female', 'male'],
                          ['from Africa', 'from Asia', 'from Europe',
                           'from US'],
                          ['uses Chrome', 'uses Firefox', 'uses IE',
                           'uses Safari']])
>>> enc.transform([['female', 'from Asia', 'uses Chrome']]).toarray()
array([[1., 0., 0., 1., 0., 0., 1., 0., 0., 0.]])

If there is a possibility that the training data might have missing categorical features, it can often be better to specify handle_unknown='infrequent_if_exist' instead of setting the categories manually as above. When handle_unknown='infrequent_if_exist' is specified and unknown categories are encountered during transform, no error will be raised but the resulting one-hot encoded columns for this feature will be all zeros or considered as an infrequent category if enabled. (handle_unknown='infrequent_if_exist' is only supported for one-hot encoding):

>>> enc = preprocessing.OneHotEncoder(handle_unknown='infrequent_if_exist')
>>> X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
>>> enc.fit(X)
OneHotEncoder(handle_unknown='infrequent_if_exist')
>>> enc.transform([['female', 'from Asia', 'uses Chrome']]).toarray()
array([[1., 0., 0., 0., 0., 0.]])

It is also possible to encode each column into n_categories - 1 columns instead of n_categories columns by using the drop parameter. This parameter allows the user to specify a category for each feature to be dropped. This is useful to avoid co-linearity in the input matrix in some classifiers. Such functionality is useful, for example, when using non-regularized regression (LinearRegression), since co-linearity would cause the covariance matrix to be non-invertible:

>>> X = [['male', 'from US', 'uses Safari'],
...      ['female', 'from Europe', 'uses Firefox']]
>>> drop_enc = preprocessing.OneHotEncoder(drop='first').fit(X)
>>> drop_enc.categories_
[array(['female', 'male'], dtype=object), array(['from Europe', 'from US'], dtype=object),
 array(['uses Firefox', 'uses Safari'], dtype=object)]
>>> drop_enc.transform(X).toarray()
array([[1., 1., 1.],
       [0., 0., 0.]])

One might want to drop one of the two columns only for features with 2 categories. In this case, you can set the parameter drop='if_binary'.

>>> X = [['male', 'US', 'Safari'],
...      ['female', 'Europe', 'Firefox'],
...      ['female', 'Asia', 'Chrome']]
>>> drop_enc = preprocessing.OneHotEncoder(drop='if_binary').fit(X)
>>> drop_enc.categories_
[array(['female', 'male'], dtype=object), array(['Asia', 'Europe', 'US'], dtype=object),
 array(['Chrome', 'Firefox', 'Safari'], dtype=object)]
>>> drop_enc.transform(X).toarray()
array([[1., 0., 0., 1., 0., 0., 1.],
       [0., 0., 1., 0., 0., 1., 0.],
       [0., 1., 0., 0., 1., 0., 0.]])

In the transformed X, the first column is the encoding of the feature with categories “male”/”female”, while the remaining 6 columns is the encoding of the 2 features with respectively 3 categories each.

When handle_unknown='ignore' and drop is not None, unknown categories will be encoded as all zeros:

>>> drop_enc = preprocessing.OneHotEncoder(drop='first',
...                                        handle_unknown='ignore').fit(X)
>>> X_test = [['unknown', 'America', 'IE']]
>>> drop_enc.transform(X_test).toarray()
array([[0., 0., 0., 0., 0.]])

All the categories in X_test are unknown during transform and will be mapped to all zeros. This means that unknown categories will have the same mapping as the dropped category. OneHotEncoder.inverse_transform will map all zeros to the dropped category if a category is dropped and None if a category is not dropped:

>>> drop_enc = preprocessing.OneHotEncoder(drop='if_binary', sparse_output=False,
...                                        handle_unknown='ignore').fit(X)
>>> X_test = [['unknown', 'America', 'IE']]
>>> X_trans = drop_enc.transform(X_test)
>>> X_trans
array([[0., 0., 0., 0., 0., 0., 0.]])
>>> drop_enc.inverse_transform(X_trans)
array([['female', None, None]], dtype=object)

OneHotEncoder supports categorical features with missing values by considering the missing values as an additional category:

>>> X = [['male', 'Safari'],
...      ['female', None],
...      [np.nan, 'Firefox']]
>>> enc = preprocessing.OneHotEncoder(handle_unknown='error').fit(X)
>>> enc.categories_
[array(['female', 'male', nan], dtype=object),
 array(['Firefox', 'Safari', None], dtype=object)]
>>> enc.transform(X).toarray()
array([[0., 1., 0., 0., 1., 0.],
       [1., 0., 0., 0., 0., 1.],
       [0., 0., 1., 1., 0., 0.]])

If a feature contains both np.nan and None, they will be considered separate categories:

>>> X = [['Safari'], [None], [np.nan], ['Firefox']]
>>> enc = preprocessing.OneHotEncoder(handle_unknown='error').fit(X)
>>> enc.categories_
[array(['Firefox', 'Safari', None, nan], dtype=object)]
>>> enc.transform(X).toarray()
array([[0., 1., 0., 0.],
       [0., 0., 1., 0.],
       [0., 0., 0., 1.],
       [1., 0., 0., 0.]])

See Loading features from dicts for categorical features that are represented as a dict, not as scalars.

6.3.4.1. Infrequent categories

OneHotEncoder and OrdinalEncoder support aggregating infrequent categories into a single output for each feature. The parameters to enable the gathering of infrequent categories are min_frequency and max_categories.

1. min_frequency is either an integer greater or equal to 1, or a float in the interval (0.0, 1.0). If min_frequency is an integer, categories with a cardinality smaller than min_frequency will be considered infrequent. If min_frequency is a float, categories with a cardinality smaller than this fraction of the total number of samples will be considered infrequent. The default value is 1, which means every category is encoded separately.

2. max_categories is either None or any integer greater than 1. This parameter sets an upper limit to the number of output features for each input feature. max_categories includes the feature that combines infrequent categories.

In the following example with OrdinalEncoder, the categories 'dog' and 'snake' are considered infrequent:

>>> X = np.array([['dog'] * 5 + ['cat'] * 20 + ['rabbit'] * 10 +
...               ['snake'] * 3], dtype=object).T
>>> enc = preprocessing.OrdinalEncoder(min_frequency=6).fit(X)
>>> enc.infrequent_categories_
[array(['dog', 'snake'], dtype=object)]
>>> enc.transform(np.array([['dog'], ['cat'], ['rabbit'], ['snake']]))
array([[2.],
       [0.],
       [1.],
       [2.]])

OrdinalEncoder’s max_categories do not take into account missing or unknown categories. Setting unknown_value or encoded_missing_value to an integer will increase the number of unique integer codes by one each. This can result in up to max_categories + 2 integer codes. In the following example, “a” and “d” are considered infrequent and grouped together into a single category, “b” and “c” are their own categories, unknown values are encoded as 3 and missing values are encoded as 4.

>>> X_train = np.array(
...     [["a"] * 5 + ["b"] * 20 + ["c"] * 10 + ["d"] * 3 + [np.nan]],
...     dtype=object).T
>>> enc = preprocessing.OrdinalEncoder(
...     handle_unknown="use_encoded_value", unknown_value=3,
...     max_categories=3, encoded_missing_value=4)
>>> _ = enc.fit(X_train)
>>> X_test = np.array([["a"], ["b"], ["c"], ["d"], ["e"], [np.nan]], dtype=object)
>>> enc.transform(X_test)
array([[2.],
       [0.],
       [1.],
       [2.],
       [3.],
       [4.]])

Similarity, OneHotEncoder can be configured to group together infrequent categories:

>>> enc = preprocessing.OneHotEncoder(min_frequency=6, sparse_output=False).fit(X)
>>> enc.infrequent_categories_
[array(['dog', 'snake'], dtype=object)]
>>> enc.transform(np.array([['dog'], ['cat'], ['rabbit'], ['snake']]))
array([[0., 0., 1.],
       [1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

By setting handle_unknown to 'infrequent_if_exist', unknown categories will be considered infrequent:

>>> enc = preprocessing.OneHotEncoder(
...    handle_unknown='infrequent_if_exist', sparse_output=False, min_frequency=6)
>>> enc = enc.fit(X)
>>> enc.transform(np.array([['dragon']]))
array([[0., 0., 1.]])

OneHotEncoder.get_feature_names_out uses ‘infrequent’ as the infrequent feature name:

>>> enc.get_feature_names_out()
array(['x0_cat', 'x0_rabbit', 'x0_infrequent_sklearn'], dtype=object)

When 'handle_unknown' is set to 'infrequent_if_exist' and an unknown category is encountered in transform:

1. If infrequent category support was not configured or there was no infrequent category during training, the resulting one-hot encoded columns for this feature will be all zeros. In the inverse transform, an unknown category will be denoted as None.

2. If there is an infrequent category during training, the unknown category will be considered infrequent. In the inverse transform, ‘infrequent_sklearn’ will be used to represent the infrequent category.

Infrequent categories can also be configured using max_categories. In the following example, we set max_categories=2 to limit the number of features in the output. This will result in all but the 'cat' category to be considered infrequent, leading to two features, one for 'cat' and one for infrequent categories - which are all the others:

>>> enc = preprocessing.OneHotEncoder(max_categories=2, sparse_output=False)
>>> enc = enc.fit(X)
>>> enc.transform([['dog'], ['cat'], ['rabbit'], ['snake']])
array([[0., 1.],
       [1., 0.],
       [0., 1.],
       [0., 1.]])

If both max_categories and min_frequency are non-default values, then categories are selected based on min_frequency first and max_categories categories are kept. In the following example, min_frequency=4 considers only snake to be infrequent, but max_categories=3, forces dog to also be infrequent:

>>> enc = preprocessing.OneHotEncoder(min_frequency=4, max_categories=3, sparse_output=False)
>>> enc = enc.fit(X)
>>> enc.transform([['dog'], ['cat'], ['rabbit'], ['snake']])
array([[0., 0., 1.],
       [1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

If there are infrequent categories with the same cardinality at the cutoff of max_categories, then then the first max_categories are taken based on lexicon ordering. In the following example, “b”, “c”, and “d”, have the same cardinality and with max_categories=2, “b” and “c” are infrequent because they have a higher lexicon order.

>>> X = np.asarray([["a"] * 20 + ["b"] * 10 + ["c"] * 10 + ["d"] * 10], dtype=object).T
>>> enc = preprocessing.OneHotEncoder(max_categories=3).fit(X)
>>> enc.infrequent_categories_
[array(['b', 'c'], dtype=object)]

6.3.4.2. Target Encoder

The TargetEncoder uses the target mean conditioned on the categorical feature for encoding unordered categories, i.e. nominal categories [PAR] [MIC]. This encoding scheme is useful with categorical features with high cardinality, where one-hot encoding would inflate the feature space making it more expensive for a downstream model to process. A classical example of high cardinality categories are location based such as zip code or region. For the binary classification target, the target encoding is given by:

\[S_i = \lambda_i\frac{n_{iY}}{n_i} + (1 - \lambda_i)\frac{n_Y}{n}\]

where \(S_i\) is the encoding for category \(i\), \(n_{iY}\) is the number of observations with \(Y=1\) and category \(i\), \(n_i\) is the number of observations with category \(i\), \(n_Y\) is the number of observations with \(Y=1\), \(n\) is the number of observations, and \(\lambda_i\) is a shrinkage factor for category \(i\). The shrinkage factor is given by:

\[\lambda_i = \frac{n_i}{m + n_i}\]

where \(m\) is a smoothing factor, which is controlled with the smooth parameter in TargetEncoder. Large smoothing factors will put more weight on the global mean. When smooth="auto", the smoothing factor is computed as an empirical Bayes estimate: \(m=\sigma_i^2/\tau^2\), where \(\sigma_i^2\) is the variance of y with category \(i\) and \(\tau^2\) is the global variance of y.

For continuous targets, the formulation is similar to binary classification:

\[S_i = \lambda_i\frac{\sum_{k\in L_i}Y_k}{n_i} + (1 - \lambda_i)\frac{\sum_{k=1}^{n}Y_k}{n}\]

where \(L_i\) is the set of observations with category \(i\) and \(n_i\) is the number of observations with category \(i\).

fit_transform internally relies on a cross fitting scheme to prevent target information from leaking into the train-time representation, especially for non-informative high-cardinality categorical variables, and help prevent the downstream model from overfitting spurious correlations. Note that as a result, fit(X, y).transform(X) does not equal fit_transform(X, y). In fit_transform, the training data is split into k folds (determined by the cv parameter) and each fold is encoded using the encodings learnt using the other k-1 folds. The following diagram shows the cross fitting scheme in fit_transform with the default cv=5:

fit_transform also learns a ‘full data’ encoding using the whole training set. This is never used in fit_transform but is saved to the attribute encodings_, for use when transform is called. Note that the encodings learned for each fold during the cross fitting scheme are not saved to an attribute.

The fit method does not use any cross fitting schemes and learns one encoding on the entire training set, which is used to encode categories in transform. This encoding is the same as the ‘full data’ encoding learned in fit_transform.

Note

TargetEncoder considers missing values, such as np.nan or None, as another category and encodes them like any other category. Categories that are not seen during fit are encoded with the target mean, i.e. target_mean_.

Examples:

• Comparing Target Encoder with Other Encoders

• Target Encoder’s Internal Cross fitting

References

[MIC]

Micci-Barreca, Daniele. “A preprocessing scheme for high-cardinality categorical attributes in classification and prediction problems” SIGKDD Explor. Newsl. 3, 1 (July 2001), 27–32.

[PAR]

Pargent, F., Pfisterer, F., Thomas, J. et al. “Regularized target encoding outperforms traditional methods in supervised machine learning with high cardinality features” Comput Stat 37, 2671–2692 (2022)

6.3.5. Discretization

Discretization (otherwise known as quantization or binning) provides a way to partition continuous features into discrete values. Certain datasets with continuous features may benefit from discretization, because discretization can transform the dataset of continuous attributes to one with only nominal attributes.

One-hot encoded discretized features can make a model more expressive, while maintaining interpretability. For instance, pre-processing with a discretizer can introduce nonlinearity to linear models. For more advanced possibilities, in particular smooth ones, see Generating polynomial features further below.

6.3.5.1. K-bins discretization

KBinsDiscretizer discretizes features into k bins:

>>> X = np.array([[ -3., 5., 15 ],
...               [  0., 6., 14 ],
...               [  6., 3., 11 ]])
>>> est = preprocessing.KBinsDiscretizer(n_bins=[3, 2, 2], encode='ordinal').fit(X)

By default the output is one-hot encoded into a sparse matrix (See Encoding categorical features) and this can be configured with the encode parameter. For each feature, the bin edges are computed during fit and together with the number of bins, they will define the intervals. Therefore, for the current example, these intervals are defined as:

• feature 1: \({[-\infty, -1), [-1, 2), [2, \infty)}\)

• feature 2: \({[-\infty, 5), [5, \infty)}\)

• feature 3: \({[-\infty, 14), [14, \infty)}\)

Based on these bin intervals, X is transformed as follows:

>>> est.transform(X)                      
array([[ 0., 1., 1.],
       [ 1., 1., 1.],
       [ 2., 0., 0.]])

The resulting dataset contains ordinal attributes which can be further used in a Pipeline.

Discretization is similar to constructing histograms for continuous data. However, histograms focus on counting features which fall into particular bins, whereas discretization focuses on assigning feature values to these bins.

KBinsDiscretizer implements different binning strategies, which can be selected with the strategy parameter. The ‘uniform’ strategy uses constant-width bins. The ‘quantile’ strategy uses the quantiles values to have equally populated bins in each feature. The ‘kmeans’ strategy defines bins based on a k-means clustering procedure performed on each feature independently.

Be aware that one can specify custom bins by passing a callable defining the discretization strategy to FunctionTransformer. For instance, we can use the Pandas function pandas.cut:

>>> import pandas as pd
>>> import numpy as np
>>> bins = [0, 1, 13, 20, 60, np.inf]
>>> labels = ['infant', 'kid', 'teen', 'adult', 'senior citizen']
>>> transformer = preprocessing.FunctionTransformer(
...     pd.cut, kw_args={'bins': bins, 'labels': labels, 'retbins': False}
... )
>>> X = np.array([0.2, 2, 15, 25, 97])
>>> transformer.fit_transform(X)
['infant', 'kid', 'teen', 'adult', 'senior citizen']
Categories (5, object): ['infant' < 'kid' < 'teen' < 'adult' < 'senior citizen']

Examples:

• Using KBinsDiscretizer to discretize continuous features

• Feature discretization

• Demonstrating the different strategies of KBinsDiscretizer

6.3.5.2. Feature binarization

Feature binarization is the process of thresholding numerical features to get boolean values. This can be useful for downstream probabilistic estimators that make assumption that the input data is distributed according to a multi-variate Bernoulli distribution. For instance, this is the case for the BernoulliRBM.

It is also common among the text processing community to use binary feature values (probably to simplify the probabilistic reasoning) even if normalized counts (a.k.a. term frequencies) or TF-IDF valued features often perform slightly better in practice.

As for the Normalizer, the utility class Binarizer is meant to be used in the early stages of Pipeline. The fit method does nothing as each sample is treated independently of others:

>>> X = [[ 1., -1.,  2.],
...      [ 2.,  0.,  0.],
...      [ 0.,  1., -1.]]

>>> binarizer = preprocessing.Binarizer().fit(X)  # fit does nothing
>>> binarizer
Binarizer()

>>> binarizer.transform(X)
array([[1., 0., 1.],
       [1., 0., 0.],
       [0., 1., 0.]])

It is possible to adjust the threshold of the binarizer:

>>> binarizer = preprocessing.Binarizer(threshold=1.1)
>>> binarizer.transform(X)
array([[0., 0., 1.],
       [1., 0., 0.],
       [0., 0., 0.]])

As for the Normalizer class, the preprocessing module provides a companion function binarize to be used when the transformer API is not necessary.

Note that the Binarizer is similar to the KBinsDiscretizer when k = 2, and when the bin edge is at the value threshold.

Sparse input

binarize and Binarizer accept both dense array-like and sparse matrices from scipy.sparse as input.

For sparse input the data is converted to the Compressed Sparse Rows representation (see scipy.sparse.csr_matrix). To avoid unnecessary memory copies, it is recommended to choose the CSR representation upstream.

6.3.6. Imputation of missing values

Tools for imputing missing values are discussed at Imputation of missing values.

6.3.7. Generating polynomial features

Often it’s useful to add complexity to a model by considering nonlinear features of the input data. We show two possibilities that are both based on polynomials: The first one uses pure polynomials, the second one uses splines, i.e. piecewise polynomials.

6.3.7.1. Polynomial features

A simple and common method to use is polynomial features, which can get features’ high-order and interaction terms. It is implemented in PolynomialFeatures:

>>> import numpy as np
>>> from sklearn.preprocessing import PolynomialFeatures
>>> X = np.arange(6).reshape(3, 2)
>>> X
array([[0, 1],
       [2, 3],
       [4, 5]])
>>> poly = PolynomialFeatures(2)
>>> poly.fit_transform(X)
array([[ 1.,  0.,  1.,  0.,  0.,  1.],
       [ 1.,  2.,  3.,  4.,  6.,  9.],
       [ 1.,  4.,  5., 16., 20., 25.]])

The features of X have been transformed from \((X_1, X_2)\) to \((1, X_1, X_2, X_1^2, X_1X_2, X_2^2)\).

In some cases, only interaction terms among features are required, and it can be gotten with the setting interaction_only=True:

>>> X = np.arange(9).reshape(3, 3)
>>> X
array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])
>>> poly = PolynomialFeatures(degree=3, interaction_only=True)
>>> poly.fit_transform(X)
array([[  1.,   0.,   1.,   2.,   0.,   0.,   2.,   0.],
       [  1.,   3.,   4.,   5.,  12.,  15.,  20.,  60.],
       [  1.,   6.,   7.,   8.,  42.,  48.,  56., 336.]])

The features of X have been transformed from \((X_1, X_2, X_3)\) to \((1, X_1, X_2, X_3, X_1X_2, X_1X_3, X_2X_3, X_1X_2X_3)\).

Note that polynomial features are used implicitly in kernel methods (e.g., SVC, KernelPCA) when using polynomial Kernel functions.

See Polynomial and Spline interpolation for Ridge regression using created polynomial features.

6.3.7.2. Spline transformer

Another way to add nonlinear terms instead of pure polynomials of features is to generate spline basis functions for each feature with the SplineTransformer. Splines are piecewise polynomials, parametrized by their polynomial degree and the positions of the knots. The SplineTransformer implements a B-spline basis, cf. the references below.

Note

The SplineTransformer treats each feature separately, i.e. it won’t give you interaction terms.

Some of the advantages of splines over polynomials are:

• B-splines are very flexible and robust if you keep a fixed low degree, usually 3, and parsimoniously adapt the number of knots. Polynomials would need a higher degree, which leads to the next point.

• B-splines do not have oscillatory behaviour at the boundaries as have polynomials (the higher the degree, the worse). This is known as Runge’s phenomenon.

• B-splines provide good options for extrapolation beyond the boundaries, i.e. beyond the range of fitted values. Have a look at the option extrapolation.

• B-splines generate a feature matrix with a banded structure. For a single feature, every row contains only degree + 1 non-zero elements, which occur consecutively and are even positive. This results in a matrix with good numerical properties, e.g. a low condition number, in sharp contrast to a matrix of polynomials, which goes under the name Vandermonde matrix. A low condition number is important for stable algorithms of linear models.

The following code snippet shows splines in action:

>>> import numpy as np
>>> from sklearn.preprocessing import SplineTransformer
>>> X = np.arange(5).reshape(5, 1)
>>> X
array([[0],
       [1],
       [2],
       [3],
       [4]])
>>> spline = SplineTransformer(degree=2, n_knots=3)
>>> spline.fit_transform(X)
array([[0.5  , 0.5  , 0.   , 0.   ],
       [0.125, 0.75 , 0.125, 0.   ],
       [0.   , 0.5  , 0.5  , 0.   ],
       [0.   , 0.125, 0.75 , 0.125],
       [0.   , 0.   , 0.5  , 0.5  ]])

As the X is sorted, one can easily see the banded matrix output. Only the three middle diagonals are non-zero for degree=2. The higher the degree, the more overlapping of the splines.

Interestingly, a SplineTransformer of degree=0 is the same as KBinsDiscretizer with encode='onehot-dense' and n_bins = n_knots - 1 if knots = strategy.

Examples:

• Polynomial and Spline interpolation

• Time-related feature engineering

References:

• Eilers, P., & Marx, B. (1996). Flexible Smoothing with B-splines and Penalties. Statist. Sci. 11 (1996), no. 2, 89–121.

• Perperoglou, A., Sauerbrei, W., Abrahamowicz, M. et al. A review of spline function procedures in R. BMC Med Res Methodol 19, 46 (2019).

6.3.8. Custom transformers

Often, you will want to convert an existing Python function into a transformer to assist in data cleaning or processing. You can implement a transformer from an arbitrary function with FunctionTransformer. For example, to build a transformer that applies a log transformation in a pipeline, do:

>>> import numpy as np
>>> from sklearn.preprocessing import FunctionTransformer
>>> transformer = FunctionTransformer(np.log1p, validate=True)
>>> X = np.array([[0, 1], [2, 3]])
>>> # Since FunctionTransformer is no-op during fit, we can call transform directly
>>> transformer.transform(X)
array([[0.        , 0.69314718],
       [1.09861229, 1.38629436]])

You can ensure that func and inverse_func are the inverse of each other by setting check_inverse=True and calling fit before transform. Please note that a warning is raised and can be turned into an error with a filterwarnings:

>>> import warnings
>>> warnings.filterwarnings("error", message=".*check_inverse*.",
...                         category=UserWarning, append=False)

For a full code example that demonstrates using a FunctionTransformer to extract features from text data see Column Transformer with Heterogeneous Data Sources and Time-related feature engineering.