`sklearn.cluster`.KMeans¶

class sklearn.cluster.KMeans(n_clusters=8, *, init='k-means++', n_init=10, max_iter=300, tol=0.0001, verbose=0, random_state=None, copy_x=True, algorithm='lloyd')[source]¶

K-Means clustering.

Read more in the User Guide.

Parameters:

n_clustersint, default=8

The number of clusters to form as well as the number of centroids to generate.

init{‘k-means++’, ‘random’}, callable or array-like of shape (n_clusters, n_features), default=’k-means++’

Method for initialization:

‘k-means++’ : selects initial cluster centroids using sampling based on an empirical probability distribution of the points’ contribution to the overall inertia. This technique speeds up convergence, and is theoretically proven to be \(\mathcal{O}(\log k)\)-optimal. See the description of n_init for more details.

‘random’: choose n_clusters observations (rows) at random from data for the initial centroids.

If an array is passed, it should be of shape (n_clusters, n_features) and gives the initial centers.

If a callable is passed, it should take arguments X, n_clusters and a random state and return an initialization.

n_initint, default=10

Number of time the k-means algorithm will be run with different centroid seeds. The final results will be the best output of n_init consecutive runs in terms of inertia.

max_iterint, default=300

Maximum number of iterations of the k-means algorithm for a single run.

tolfloat, default=1e-4

Relative tolerance with regards to Frobenius norm of the difference in the cluster centers of two consecutive iterations to declare convergence.

verboseint, default=0

Verbosity mode.

random_stateint, RandomState instance or None, default=None

Determines random number generation for centroid initialization. Use an int to make the randomness deterministic. See Glossary.

copy_xbool, default=True

When pre-computing distances it is more numerically accurate to center the data first. If copy_x is True (default), then the original data is not modified. If False, the original data is modified, and put back before the function returns, but small numerical differences may be introduced by subtracting and then adding the data mean. Note that if the original data is not C-contiguous, a copy will be made even if copy_x is False. If the original data is sparse, but not in CSR format, a copy will be made even if copy_x is False.

algorithm{“lloyd”, “elkan”, “auto”, “full”}, default=”lloyd”

K-means algorithm to use. The classical EM-style algorithm is "lloyd". The "elkan" variation can be more efficient on some datasets with well-defined clusters, by using the triangle inequality. However it’s more memory intensive due to the allocation of an extra array of shape (n_samples, n_clusters).

"auto" and "full" are deprecated and they will be removed in Scikit-Learn 1.3. They are both aliases for "lloyd".

Changed in version 0.18: Added Elkan algorithm

Changed in version 1.1: Renamed “full” to “lloyd”, and deprecated “auto” and “full”. Changed “auto” to use “lloyd” instead of “elkan”.

Attributes:

cluster_centers_ndarray of shape (n_clusters, n_features): Coordinates of cluster centers. If the algorithm stops before fully converging (see tol and max_iter), these will not be consistent with labels_.
labels_ndarray of shape (n_samples,): Labels of each point
inertia_float: Sum of squared distances of samples to their closest cluster center, weighted by the sample weights if provided.
n_iter_int: Number of iterations run.
n_features_in_int: Number of features seen during fit.

New in version 0.24.
feature_names_in_ndarray of shape (n_features_in_,): Names of features seen during fit. Defined only when X has feature names that are all strings.

New in version 1.0.

See also

MiniBatchKMeans: Alternative online implementation that does incremental updates of the centers positions using mini-batches. For large scale learning (say n_samples > 10k) MiniBatchKMeans is probably much faster than the default batch implementation.

Notes

The k-means problem is solved using either Lloyd’s or Elkan’s algorithm.

The average complexity is given by O(k n T), where n is the number of samples and T is the number of iteration.

The worst case complexity is given by O(n^(k+2/p)) with n = n_samples, p = n_features. (D. Arthur and S. Vassilvitskii, ‘How slow is the k-means method?’ SoCG2006)

In practice, the k-means algorithm is very fast (one of the fastest clustering algorithms available), but it falls in local minima. That’s why it can be useful to restart it several times.

If the algorithm stops before fully converging (because of tol or max_iter), labels_ and cluster_centers_ will not be consistent, i.e. the cluster_centers_ will not be the means of the points in each cluster. Also, the estimator will reassign labels_ after the last iteration to make labels_ consistent with predict on the training set.

Examples

>>> from sklearn.cluster import KMeans
>>> import numpy as np
>>> X = np.array([[1, 2], [1, 4], [1, 0],
...               [10, 2], [10, 4], [10, 0]])
>>> kmeans = KMeans(n_clusters=2, random_state=0).fit(X)
>>> kmeans.labels_
array([1, 1, 1, 0, 0, 0], dtype=int32)
>>> kmeans.predict([[0, 0], [12, 3]])
array([1, 0], dtype=int32)
>>> kmeans.cluster_centers_
array([[10.,  2.],
       [ 1.,  2.]])

Methods

`fit`(X[, y, sample_weight])	Compute k-means clustering.
`fit_predict`(X[, y, sample_weight])	Compute cluster centers and predict cluster index for each sample.
`fit_transform`(X[, y, sample_weight])	Compute clustering and transform X to cluster-distance space.
`get_feature_names_out`([input_features])	Get output feature names for transformation.
`get_params`([deep])	Get parameters for this estimator.
`predict`(X[, sample_weight])	Predict the closest cluster each sample in X belongs to.
`score`(X[, y, sample_weight])	Opposite of the value of X on the K-means objective.
`set_params`(**params)	Set the parameters of this estimator.
`transform`(X)	Transform X to a cluster-distance space.

fit(X, y=None, sample_weight=None)[source]¶

Compute k-means clustering.

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features): Training instances to cluster. It must be noted that the data will be converted to C ordering, which will cause a memory copy if the given data is not C-contiguous. If a sparse matrix is passed, a copy will be made if it’s not in CSR format.
yIgnored: Not used, present here for API consistency by convention.
sample_weightarray-like of shape (n_samples,), default=None: The weights for each observation in X. If None, all observations are assigned equal weight.

New in version 0.20.

Returns:

selfobject: Fitted estimator.

fit_predict(X, y=None, sample_weight=None)[source]¶

Compute cluster centers and predict cluster index for each sample.

Convenience method; equivalent to calling fit(X) followed by predict(X).

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features): New data to transform.
yIgnored: Not used, present here for API consistency by convention.
sample_weightarray-like of shape (n_samples,), default=None: The weights for each observation in X. If None, all observations are assigned equal weight.

Returns:

labelsndarray of shape (n_samples,): Index of the cluster each sample belongs to.

fit_transform(X, y=None, sample_weight=None)[source]¶

Compute clustering and transform X to cluster-distance space.

Equivalent to fit(X).transform(X), but more efficiently implemented.

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features): New data to transform.
yIgnored: Not used, present here for API consistency by convention.
sample_weightarray-like of shape (n_samples,), default=None: The weights for each observation in X. If None, all observations are assigned equal weight.

Returns:

X_newndarray of shape (n_samples, n_clusters): X transformed in the new space.

get_feature_names_out(input_features=None)[source]¶

Get output feature names for transformation.

Parameters:

input_featuresarray-like of str or None, default=None: Only used to validate feature names with the names seen in fit.

Returns:

feature_names_outndarray of str objects: Transformed feature names.

get_params(deep=True)[source]¶

Get parameters for this estimator.

Parameters:

deepbool, default=True: If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

paramsdict: Parameter names mapped to their values.

predict(X, sample_weight=None)[source]¶

Predict the closest cluster each sample in X belongs to.

In the vector quantization literature, cluster_centers_ is called the code book and each value returned by predict is the index of the closest code in the code book.

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features): New data to predict.
sample_weightarray-like of shape (n_samples,), default=None: The weights for each observation in X. If None, all observations are assigned equal weight.

Returns:

labelsndarray of shape (n_samples,): Index of the cluster each sample belongs to.

score(X, y=None, sample_weight=None)[source]¶

Opposite of the value of X on the K-means objective.

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features): New data.
yIgnored: Not used, present here for API consistency by convention.
sample_weightarray-like of shape (n_samples,), default=None: The weights for each observation in X. If None, all observations are assigned equal weight.

Returns:

scorefloat: Opposite of the value of X on the K-means objective.

set_params(**params)[source]¶

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as Pipeline). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters:

**paramsdict: Estimator parameters.

Returns:

selfestimator instance: Estimator instance.

transform(X)[source]¶

Transform X to a cluster-distance space.

In the new space, each dimension is the distance to the cluster centers. Note that even if X is sparse, the array returned by transform will typically be dense.

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features): New data to transform.

Returns:

X_newndarray of shape (n_samples, n_clusters): X transformed in the new space.

Examples using `sklearn.cluster.KMeans`¶

Release Highlights for scikit-learn 1.1

Release Highlights for scikit-learn 0.23

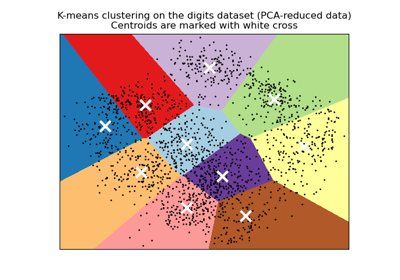
A demo of K-Means clustering on the handwritten digits data

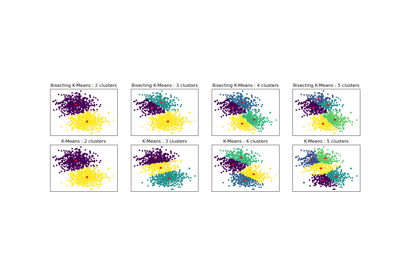
Bisecting K-Means and Regular K-Means Performance Comparison

Color Quantization using K-Means

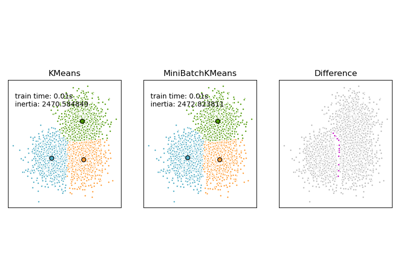
Comparison of the K-Means and MiniBatchKMeans clustering algorithms

Demonstration of k-means assumptions

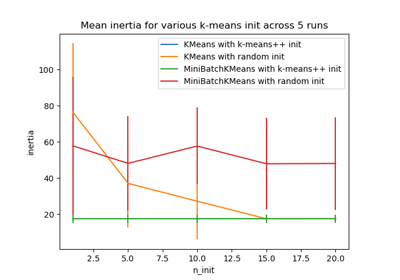
Empirical evaluation of the impact of k-means initialization

K-means Clustering

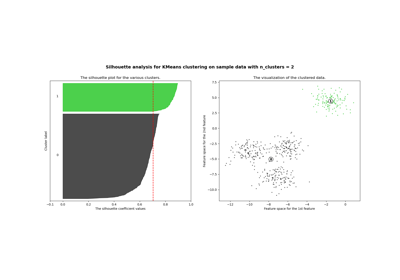
Selecting the number of clusters with silhouette analysis on KMeans clustering

Vector Quantization Example

Clustering text documents using k-means

sklearn.cluster.KMeans¶

Examples using sklearn.cluster.KMeans¶

`sklearn.cluster`.KMeans¶

Examples using `sklearn.cluster.KMeans`¶