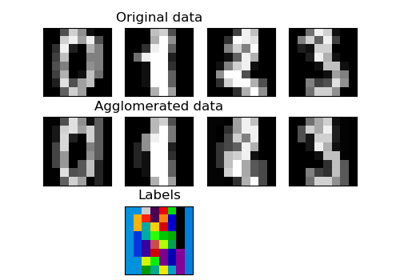
sklearn.cluster.FeatureAgglomeration

class sklearn.cluster.FeatureAgglomeration(n_clusters=2, *, affinity='euclidean', memory=None, connectivity=None, compute_full_tree='auto', linkage='ward', pooling_func=<function mean>, distance_threshold=None, compute_distances=False)

Agglomerate features.

Recursively merges pair of clusters of features.

Read more in the User Guide.

Parameters:

n_clustersint, default=2

The number of clusters to find. It must be None if distance_threshold is not None.

affinitystr or callable, default=’euclidean’

Metric used to compute the linkage. Can be “euclidean”, “l1”, “l2”, “manhattan”, “cosine”, or ‘precomputed’. If linkage is “ward”, only “euclidean” is accepted.

memorystr or object with the joblib.Memory interface, default=None

Used to cache the output of the computation of the tree. By default, no caching is done. If a string is given, it is the path to the caching directory.

connectivityarray-like or callable, default=None

Connectivity matrix. Defines for each feature the neighboring features following a given structure of the data. This can be a connectivity matrix itself or a callable that transforms the data into a connectivity matrix, such as derived from kneighbors_graph. Default is None, i.e, the hierarchical clustering algorithm is unstructured.

compute_full_tree‘auto’ or bool, default=’auto’

Stop early the construction of the tree at n_clusters. This is useful to decrease computation time if the number of clusters is not small compared to the number of features. This option is useful only when specifying a connectivity matrix. Note also that when varying the number of clusters and using caching, it may be advantageous to compute the full tree. It must be True if distance_threshold is not None. By default compute_full_tree is “auto”, which is equivalent to True when distance_threshold is not None or that n_clusters is inferior to the maximum between 100 or 0.02 * n_samples. Otherwise, “auto” is equivalent to False.

linkage{“ward”, “complete”, “average”, “single”}, default=”ward”

Which linkage criterion to use. The linkage criterion determines which distance to use between sets of features. The algorithm will merge the pairs of cluster that minimize this criterion.

• “ward” minimizes the variance of the clusters being merged.

• “complete” or maximum linkage uses the maximum distances between all features of the two sets.

• “average” uses the average of the distances of each feature of the two sets.

• “single” uses the minimum of the distances between all features of the two sets.

pooling_funccallable, default=np.mean

This combines the values of agglomerated features into a single value, and should accept an array of shape [M, N] and the keyword argument axis=1, and reduce it to an array of size [M].

distance_thresholdfloat, default=None

The linkage distance threshold above which, clusters will not be merged. If not None, n_clusters must be None and compute_full_tree must be True.

New in version 0.21.

compute_distancesbool, default=False

Computes distances between clusters even if distance_threshold is not used. This can be used to make dendrogram visualization, but introduces a computational and memory overhead.

New in version 0.24.

Attributes:

n_clusters_int

The number of clusters found by the algorithm. If distance_threshold=None, it will be equal to the given n_clusters.

labels_array-like of (n_features,)

Cluster labels for each feature.

n_leaves_int

Number of leaves in the hierarchical tree.

n_connected_components_int

The estimated number of connected components in the graph.

New in version 0.21: n_connected_components_ was added to replace n_components_.

n_features_in_int

Number of features seen during fit.

New in version 0.24.

feature_names_in_ndarray of shape (n_features_in_,)

Names of features seen during fit. Defined only when X has feature names that are all strings.

New in version 1.0.

children_array-like of shape (n_nodes-1, 2)

The children of each non-leaf node. Values less than n_features correspond to leaves of the tree which are the original samples. A node i greater than or equal to n_features is a non-leaf node and has children children_[i - n_features]. Alternatively at the i-th iteration, children[i][0] and children[i][1] are merged to form node n_features + i.

distances_array-like of shape (n_nodes-1,)

Distances between nodes in the corresponding place in children_. Only computed if distance_threshold is used or compute_distances is set to True.

See also

AgglomerativeClustering

Agglomerative clustering samples instead of features.

ward_tree

Hierarchical clustering with ward linkage.

Examples

>>> import numpy as np
>>> from sklearn import datasets, cluster
>>> digits = datasets.load_digits()
>>> images = digits.images
>>> X = np.reshape(images, (len(images), -1))
>>> agglo = cluster.FeatureAgglomeration(n_clusters=32)
>>> agglo.fit(X)
FeatureAgglomeration(n_clusters=32)
>>> X_reduced = agglo.transform(X)
>>> X_reduced.shape
(1797, 32)

Methods

fit(X[, y])	Fit the hierarchical clustering on the data.
fit_transform(X[, y])	Fit to data, then transform it.
get_feature_names_out([input_features])	Get output feature names for transformation.
get_params([deep])	Get parameters for this estimator.
inverse_transform(Xred)	Inverse the transformation and return a vector of size n_features.
set_params(**params)	Set the parameters of this estimator.
transform(X)	Transform a new matrix using the built clustering.

fit(X, y=None)

Fit the hierarchical clustering on the data.

Parameters:

Xarray-like of shape (n_samples, n_features)

The data.

yIgnored

Not used, present here for API consistency by convention.

Returns:

selfobject

Returns the transformer.

property fit_predict

Fit and return the result of each sample’s clustering assignment.

fit_transform(X, y=None, **fit_params)

Fit to data, then transform it.

Fits transformer to X and y with optional parameters fit_params and returns a transformed version of X.

Parameters:

Xarray-like of shape (n_samples, n_features)

Input samples.

yarray-like of shape (n_samples,) or (n_samples, n_outputs), default=None

Target values (None for unsupervised transformations).

**fit_paramsdict

Additional fit parameters.

Returns:

X_newndarray array of shape (n_samples, n_features_new)

Transformed array.

get_feature_names_out(input_features=None)

Get output feature names for transformation.

Parameters:

input_featuresarray-like of str or None, default=None

Only used to validate feature names with the names seen in fit.

Returns:

feature_names_outndarray of str objects

Transformed feature names.

get_params(deep=True)

Get parameters for this estimator.

Parameters:

deepbool, default=True

If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

paramsdict

Parameter names mapped to their values.

inverse_transform(Xred)

Inverse the transformation and return a vector of size n_features.

Parameters:

Xredarray-like of shape (n_samples, n_clusters) or (n_clusters,)

The values to be assigned to each cluster of samples.

Returns:

Xndarray of shape (n_samples, n_features) or (n_features,)

A vector of size n_samples with the values of Xred assigned to each of the cluster of samples.

set_params(**params)

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as Pipeline). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters:

**paramsdict

Estimator parameters.

Returns:

selfestimator instance

Estimator instance.

transform(X)

Transform a new matrix using the built clustering.

Parameters:

Xarray-like of shape (n_samples, n_features) or (n_samples, n_samples)

A M by N array of M observations in N dimensions or a length M array of M one-dimensional observations.

Returns:

Yndarray of shape (n_samples, n_clusters) or (n_clusters,)

The pooled values for each feature cluster.

Examples using sklearn.cluster.FeatureAgglomeration

Feature agglomeration

Feature agglomeration

Feature agglomeration vs. univariate selection

Feature agglomeration vs. univariate selection