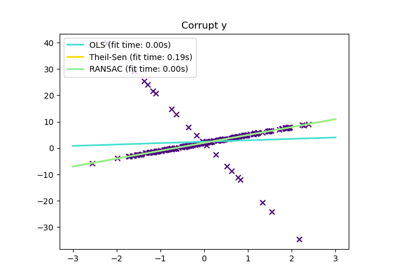
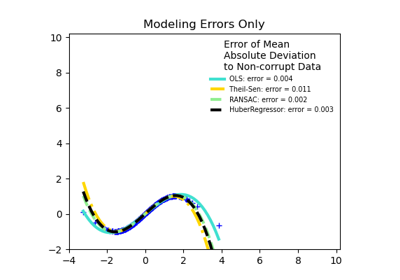
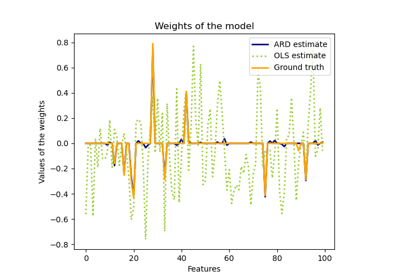
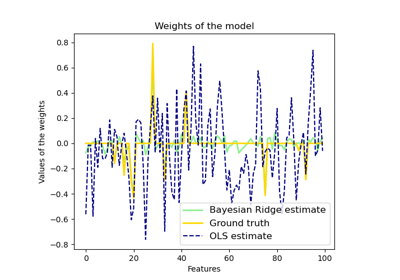
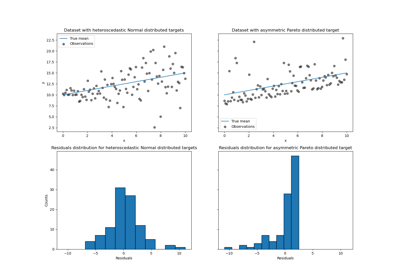
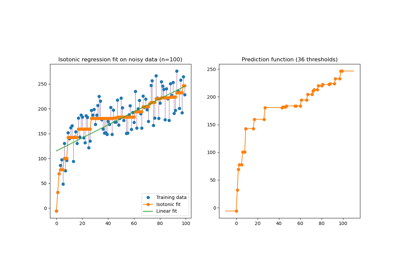
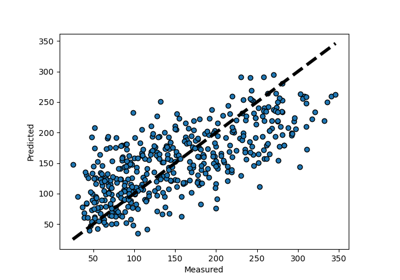
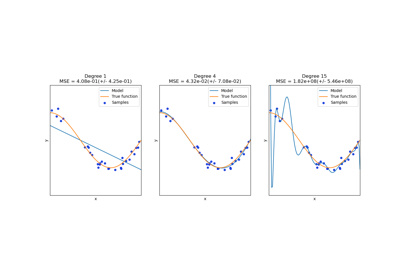
`sklearn.linear_model`.LinearRegression¶

class sklearn.linear_model.LinearRegression(*, fit_intercept=True, normalize='deprecated', copy_X=True, n_jobs=None, positive=False)[source]¶

Ordinary least squares Linear Regression.

LinearRegression fits a linear model with coefficients w = (w1, …, wp) to minimize the residual sum of squares between the observed targets in the dataset, and the targets predicted by the linear approximation.

Parameters

fit_interceptbool, default=True: Whether to calculate the intercept for this model. If set to False, no intercept will be used in calculations (i.e. data is expected to be centered).
normalizebool, default=False: This parameter is ignored when fit_intercept is set to False. If True, the regressors X will be normalized before regression by subtracting the mean and dividing by the l2-norm. If you wish to standardize, please use StandardScaler before calling fit on an estimator with normalize=False.

Deprecated since version 1.0: normalize was deprecated in version 1.0 and will be removed in 1.2.
copy_Xbool, default=True: If True, X will be copied; else, it may be overwritten.
n_jobsint, default=None: The number of jobs to use for the computation. This will only provide speedup in case of sufficiently large problems, that is if firstly n_targets > 1 and secondly X is sparse or if positive is set to True. None means 1 unless in a joblib.parallel_backend context. -1 means using all processors. See Glossary for more details.
positivebool, default=False: When set to True, forces the coefficients to be positive. This option is only supported for dense arrays.

New in version 0.24.

Attributes

coef_array of shape (n_features, ) or (n_targets, n_features): Estimated coefficients for the linear regression problem. If multiple targets are passed during the fit (y 2D), this is a 2D array of shape (n_targets, n_features), while if only one target is passed, this is a 1D array of length n_features.
rank_int: Rank of matrix X. Only available when X is dense.
singular_array of shape (min(X, y),): Singular values of X. Only available when X is dense.
intercept_float or array of shape (n_targets,): Independent term in the linear model. Set to 0.0 if fit_intercept = False.
n_features_in_int: Number of features seen during fit.

New in version 0.24.
feature_names_in_ndarray of shape (n_features_in_,): Names of features seen during fit. Defined only when X has feature names that are all strings.

New in version 1.0.

See also

Ridge: Ridge regression addresses some of the problems of Ordinary Least Squares by imposing a penalty on the size of the coefficients with l2 regularization.
Lasso: The Lasso is a linear model that estimates sparse coefficients with l1 regularization.
ElasticNet: Elastic-Net is a linear regression model trained with both l1 and l2 -norm regularization of the coefficients.

Notes

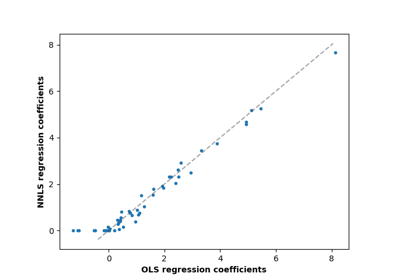
From the implementation point of view, this is just plain Ordinary Least Squares (scipy.linalg.lstsq) or Non Negative Least Squares (scipy.optimize.nnls) wrapped as a predictor object.

Examples

>>> import numpy as np
>>> from sklearn.linear_model import LinearRegression
>>> X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])
>>> # y = 1 * x_0 + 2 * x_1 + 3
>>> y = np.dot(X, np.array([1, 2])) + 3
>>> reg = LinearRegression().fit(X, y)
>>> reg.score(X, y)
1.0
>>> reg.coef_
array([1., 2.])
>>> reg.intercept_
3.0...
>>> reg.predict(np.array([[3, 5]]))
array([16.])

Methods

`fit`(X, y[, sample_weight])	Fit linear model.
`get_params`([deep])	Get parameters for this estimator.
`predict`(X)	Predict using the linear model.
`score`(X, y[, sample_weight])	Return the coefficient of determination of the prediction.
`set_params`(**params)	Set the parameters of this estimator.

fit(X, y, sample_weight=None)[source]¶

Fit linear model.

Parameters

X{array-like, sparse matrix} of shape (n_samples, n_features): Training data.
yarray-like of shape (n_samples,) or (n_samples, n_targets): Target values. Will be cast to X’s dtype if necessary.
sample_weightarray-like of shape (n_samples,), default=None: Individual weights for each sample.

New in version 0.17: parameter sample_weight support to LinearRegression.

Returns

selfobject: Fitted Estimator.

get_params(deep=True)[source]¶

Get parameters for this estimator.

Parameters

deepbool, default=True: If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns

paramsdict: Parameter names mapped to their values.

predict(X)[source]¶

Predict using the linear model.

Parameters

Xarray-like or sparse matrix, shape (n_samples, n_features): Samples.

Returns

Carray, shape (n_samples,): Returns predicted values.

score(X, y, sample_weight=None)[source]¶

Return the coefficient of determination of the prediction.

The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares ((y_true - y_pred)** 2).sum() and \(v\) is the total sum of squares ((y_true - y_true.mean()) ** 2).sum(). The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of y, disregarding the input features, would get a \(R^2\) score of 0.0.

Parameters

Xarray-like of shape (n_samples, n_features): Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape (n_samples, n_samples_fitted), where n_samples_fitted is the number of samples used in the fitting for the estimator.
yarray-like of shape (n_samples,) or (n_samples, n_outputs): True values for X.
sample_weightarray-like of shape (n_samples,), default=None: Sample weights.

Returns

scorefloat: \(R^2\) of self.predict(X) wrt. y.

Notes

The \(R^2\) score used when calling score on a regressor uses multioutput='uniform_average' from version 0.23 to keep consistent with default value of r2_score. This influences the score method of all the multioutput regressors (except for MultiOutputRegressor).

set_params(**params)[source]¶

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as Pipeline). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters

**paramsdict: Estimator parameters.

Returns

selfestimator instance: Estimator instance.

Examples using `sklearn.linear_model.LinearRegression`¶

sklearn.linear_model.LinearRegression¶

Examples using sklearn.linear_model.LinearRegression¶

`sklearn.linear_model`.LinearRegression¶

Examples using `sklearn.linear_model.LinearRegression`¶