Note

Click here to download the full example code or to run this example in your browser via Binder

Map data to a normal distribution¶

This example demonstrates the use of the Box-Cox and Yeo-Johnson transforms through PowerTransformer to map data from various distributions to a normal distribution.

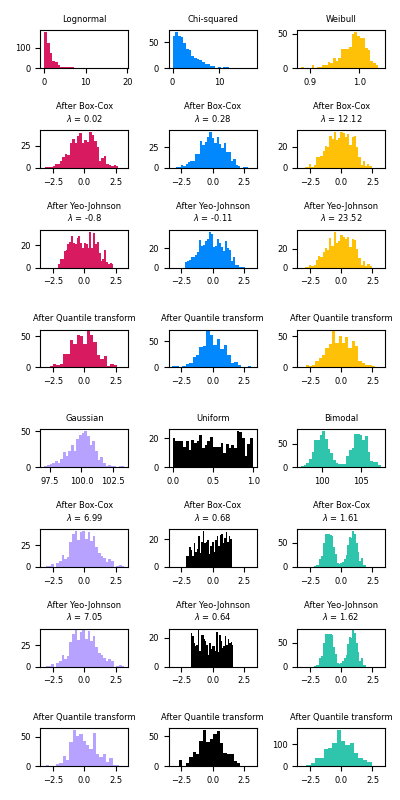
The power transform is useful as a transformation in modeling problems where homoscedasticity and normality are desired. Below are examples of Box-Cox and Yeo-Johnwon applied to six different probability distributions: Lognormal, Chi-squared, Weibull, Gaussian, Uniform, and Bimodal.

Note that the transformations successfully map the data to a normal distribution when applied to certain datasets, but are ineffective with others. This highlights the importance of visualizing the data before and after transformation.

Also note that even though Box-Cox seems to perform better than Yeo-Johnson for lognormal and chi-squared distributions, keep in mind that Box-Cox does not support inputs with negative values.

For comparison, we also add the output from QuantileTransformer. It can force any arbitrary distribution into a gaussian, provided that there are enough training samples (thousands). Because it is a non-parametric method, it is harder to interpret than the parametric ones (Box-Cox and Yeo-Johnson).

On “small” datasets (less than a few hundred points), the quantile transformer is prone to overfitting. The use of the power transform is then recommended.

$Lognormal, Chi-squared, Weibull, After Box-Cox $\lambda$ = 0.02, After Box-Cox $\lambda$ = 0.28, After Box-Cox $\lambda$ = 12.12, After Yeo-Johnson $\lambda$ = -0.8, After Yeo-Johnson $\lambda$ = -0.11, After Yeo-Johnson $\lambda$ = 23.52, After Quantile transform, After Quantile transform, After Quantile transform, Gaussian, Uniform, Bimodal, After Box-Cox $\lambda$ = 6.99, After Box-Cox $\lambda$ = 0.68, After Box-Cox $\lambda$ = 1.61, After Yeo-Johnson $\lambda$ = 7.05, After Yeo-Johnson $\lambda$ = 0.64, After Yeo-Johnson $\lambda$ = 1.62, After Quantile transform, After Quantile transform, After Quantile transform$

# Author: Eric Chang <ericchang2017@u.northwestern.edu>
#         Nicolas Hug <contact@nicolas-hug.com>
# License: BSD 3 clause

import numpy as np
import matplotlib.pyplot as plt

from sklearn.preprocessing import PowerTransformer
from sklearn.preprocessing import QuantileTransformer
from sklearn.model_selection import train_test_split

print(__doc__)


N_SAMPLES = 1000
FONT_SIZE = 6
BINS = 30


rng = np.random.RandomState(304)
bc = PowerTransformer(method='box-cox')
yj = PowerTransformer(method='yeo-johnson')
# n_quantiles is set to the training set size rather than the default value
# to avoid a warning being raised by this example
qt = QuantileTransformer(n_quantiles=500, output_distribution='normal',
                         random_state=rng)
size = (N_SAMPLES, 1)


# lognormal distribution
X_lognormal = rng.lognormal(size=size)

# chi-squared distribution
df = 3
X_chisq = rng.chisquare(df=df, size=size)

# weibull distribution
a = 50
X_weibull = rng.weibull(a=a, size=size)

# gaussian distribution
loc = 100
X_gaussian = rng.normal(loc=loc, size=size)

# uniform distribution
X_uniform = rng.uniform(low=0, high=1, size=size)

# bimodal distribution
loc_a, loc_b = 100, 105
X_a, X_b = rng.normal(loc=loc_a, size=size), rng.normal(loc=loc_b, size=size)
X_bimodal = np.concatenate([X_a, X_b], axis=0)


# create plots
distributions = [
    ('Lognormal', X_lognormal),
    ('Chi-squared', X_chisq),
    ('Weibull', X_weibull),
    ('Gaussian', X_gaussian),
    ('Uniform', X_uniform),
    ('Bimodal', X_bimodal)
]

colors = ['#D81B60', '#0188FF', '#FFC107',
          '#B7A2FF', '#000000', '#2EC5AC']

fig, axes = plt.subplots(nrows=8, ncols=3, figsize=plt.figaspect(2))
axes = axes.flatten()
axes_idxs = [(0, 3, 6, 9), (1, 4, 7, 10), (2, 5, 8, 11), (12, 15, 18, 21),
             (13, 16, 19, 22), (14, 17, 20, 23)]
axes_list = [(axes[i], axes[j], axes[k], axes[l])
             for (i, j, k, l) in axes_idxs]


for distribution, color, axes in zip(distributions, colors, axes_list):
    name, X = distribution
    X_train, X_test = train_test_split(X, test_size=.5)

    # perform power transforms and quantile transform
    X_trans_bc = bc.fit(X_train).transform(X_test)
    lmbda_bc = round(bc.lambdas_[0], 2)
    X_trans_yj = yj.fit(X_train).transform(X_test)
    lmbda_yj = round(yj.lambdas_[0], 2)
    X_trans_qt = qt.fit(X_train).transform(X_test)

    ax_original, ax_bc, ax_yj, ax_qt = axes

    ax_original.hist(X_train, color=color, bins=BINS)
    ax_original.set_title(name, fontsize=FONT_SIZE)
    ax_original.tick_params(axis='both', which='major', labelsize=FONT_SIZE)

    for ax, X_trans, meth_name, lmbda in zip(
            (ax_bc, ax_yj, ax_qt),
            (X_trans_bc, X_trans_yj, X_trans_qt),
            ('Box-Cox', 'Yeo-Johnson', 'Quantile transform'),
            (lmbda_bc, lmbda_yj, None)):
        ax.hist(X_trans, color=color, bins=BINS)
        title = 'After {}'.format(meth_name)
        if lmbda is not None:
            title += '\n$\\lambda$ = {}'.format(lmbda)
        ax.set_title(title, fontsize=FONT_SIZE)
        ax.tick_params(axis='both', which='major', labelsize=FONT_SIZE)
        ax.set_xlim([-3.5, 3.5])


plt.tight_layout()
plt.show()

Total running time of the script: ( 0 minutes 2.230 seconds)

Gallery generated by Sphinx-Gallery