1.12. Multiclass and multioutput algorithms

This section of the user guide covers functionality related to multi-learning problems, including multiclass, multilabel, and multioutput classification and regression.

The modules in this section implement meta-estimators, which require a base estimator to be provided in their constructor. Meta-estimators extend the functionality of the base estimator to support multi-learning problems, which is accomplished by transforming the multi-learning problem into a set of simpler problems, then fitting one estimator per problem.

This section covers two modules: sklearn.multiclass and sklearn.multioutput. The chart below demonstrates the problem types that each module is responsible for, and the corresponding meta-estimators that each module provides.

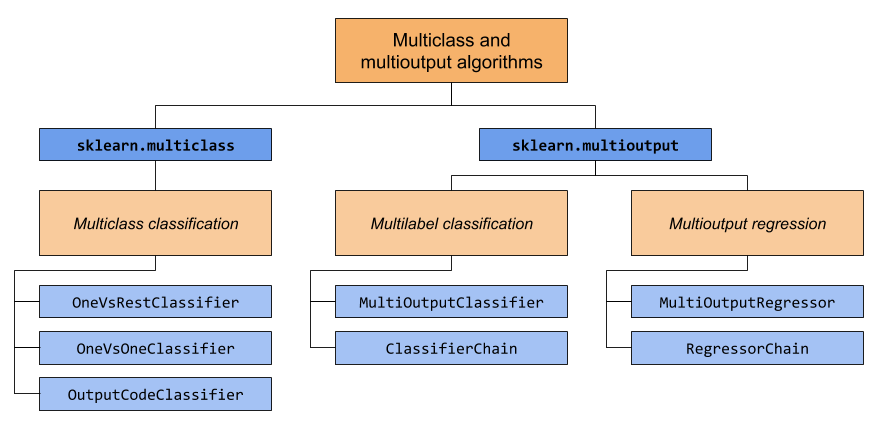
../_images/multi_org_chart.png

The table below provides a quick reference on the differences between problem types. More detailed explanations can be found in subsequent sections of this guide.

Number of targets

Target cardinality

Valid type_of_target

Multiclass classification

1

>2

‘multiclass’

Multilabel classification

>1

2 (0 or 1)

‘multilabel-indicator’

Multiclass-multioutput classification

>1

>2

‘multiclass-multioutput’

Multioutput regression

>1

Continuous

‘continuous-multioutput’

Below is a summary of scikit-learn estimators that have multi-learning support built-in, grouped by strategy. You don’t need the meta-estimators provided by this section if you’re using one of these estimators. However, meta-estimators can provide additional strategies beyond what is built-in:

1.12.1. Multiclass classification

Warning

All classifiers in scikit-learn do multiclass classification out-of-the-box. You don’t need to use the sklearn.multiclass module unless you want to experiment with different multiclass strategies.

Multiclass classification is a classification task with more than two classes. Each sample can only be labeled as one class.

For example, classification using features extracted from a set of images of fruit, where each image may either be of an orange, an apple, or a pear. Each image is one sample and is labeled as one of the 3 possible classes. Multiclass classification makes the assumption that each sample is assigned to one and only one label - one sample cannot, for example, be both a pear and an apple.

While all scikit-learn classifiers are capable of multiclass classification, the meta-estimators offered by sklearn.multiclass permit changing the way they handle more than two classes because this may have an effect on classifier performance (either in terms of generalization error or required computational resources).

1.12.1.1. Target format

Valid multiclass representations for type_of_target (y) are:

  • 1d or column vector containing more than two discrete values. An example of a vector y for 4 samples:

    >>> import numpy as np
>>> y = np.array(['apple', 'pear', 'apple', 'orange'])
>>> print(y)
['apple' 'pear' 'apple' 'orange']

  • Dense or sparse binary matrix of shape (n_samples, n_classes) with a single sample per row, where each column represents one class. An example of both a dense and sparse binary matrix y for 4 samples, where the columns, in order, are apple, orange, and pear:

    >>> import numpy as np
>>> from sklearn.preprocessing import LabelBinarizer
>>> y = np.array(['apple', 'pear', 'apple', 'orange'])
>>> y_dense = LabelBinarizer().fit_transform(y)
>>> print(y_dense)
[[1 0 0]
 [0 0 1]
 [1 0 0]
 [0 1 0]]
>>> from scipy import sparse
>>> y_sparse = sparse.csr_matrix(y_dense)
>>> print(y_sparse)
  (0, 0)    1
  (1, 2)    1
  (2, 0)    1
  (3, 1)    1

For more information about LabelBinarizer, refer to Transforming the prediction target (y).

1.12.1.2. OneVsRestClassifier

The one-vs-rest strategy, also known as one-vs-all, is implemented in OneVsRestClassifier. The strategy consists in fitting one classifier per class. For each classifier, the class is fitted against all the other classes. In addition to its computational efficiency (only n_classes classifiers are needed), one advantage of this approach is its interpretability. Since each class is represented by one and only one classifier, it is possible to gain knowledge about the class by inspecting its corresponding classifier. This is the most commonly used strategy and is a fair default choice.

Below is an example of multiclass learning using OvR:

>>> from sklearn import datasets
>>> from sklearn.multiclass import OneVsRestClassifier
>>> from sklearn.svm import LinearSVC
>>> X, y = datasets.load_iris(return_X_y=True)
>>> OneVsRestClassifier(LinearSVC(dual="auto", random_state=0)).fit(X, y).predict(X)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 1, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

OneVsRestClassifier also supports multilabel classification. To use this feature, feed the classifier an indicator matrix, in which cell [i, j] indicates the presence of label j in sample i.

../_images/sphx_glr_plot_multilabel_001.png

1.12.1.3. OneVsOneClassifier

OneVsOneClassifier constructs one classifier per pair of classes. At prediction time, the class which received the most votes is selected. In the event of a tie (among two classes with an equal number of votes), it selects the class with the highest aggregate classification confidence by summing over the pair-wise classification confidence levels computed by the underlying binary classifiers.

Since it requires to fit n_classes * (n_classes - 1) / 2 classifiers, this method is usually slower than one-vs-the-rest, due to its O(n_classes^2) complexity. However, this method may be advantageous for algorithms such as kernel algorithms which don’t scale well with n_samples. This is because each individual learning problem only involves a small subset of the data whereas, with one-vs-the-rest, the complete dataset is used n_classes times. The decision function is the result of a monotonic transformation of the one-versus-one classification.

Below is an example of multiclass learning using OvO:

>>> from sklearn import datasets
>>> from sklearn.multiclass import OneVsOneClassifier
>>> from sklearn.svm import LinearSVC
>>> X, y = datasets.load_iris(return_X_y=True)
>>> OneVsOneClassifier(LinearSVC(dual="auto", random_state=0)).fit(X, y).predict(X)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 2, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

1.12.1.4. OutputCodeClassifier

Error-Correcting Output Code-based strategies are fairly different from one-vs-the-rest and one-vs-one. With these strategies, each class is represented in a Euclidean space, where each dimension can only be 0 or 1. Another way to put it is that each class is represented by a binary code (an array of 0 and 1). The matrix which keeps track of the location/code of each class is called the code book. The code size is the dimensionality of the aforementioned space. Intuitively, each class should be represented by a code as unique as possible and a good code book should be designed to optimize classification accuracy. In this implementation, we simply use a randomly-generated code book as advocated in [3] although more elaborate methods may be added in the future.

At fitting time, one binary classifier per bit in the code book is fitted. At prediction time, the classifiers are used to project new points in the class space and the class closest to the points is chosen.

In OutputCodeClassifier, the code_size attribute allows the user to control the number of classifiers which will be used. It is a percentage of the total number of classes.

A number between 0 and 1 will require fewer classifiers than one-vs-the-rest. In theory, log2(n_classes) / n_classes is sufficient to represent each class unambiguously. However, in practice, it may not lead to good accuracy since log2(n_classes) is much smaller than n_classes.

A number greater than 1 will require more classifiers than one-vs-the-rest. In this case, some classifiers will in theory correct for the mistakes made by other classifiers, hence the name “error-correcting”. In practice, however, this may not happen as classifier mistakes will typically be correlated. The error-correcting output codes have a similar effect to bagging.

Below is an example of multiclass learning using Output-Codes:

>>> from sklearn import datasets
>>> from sklearn.multiclass import OutputCodeClassifier
>>> from sklearn.svm import LinearSVC
>>> X, y = datasets.load_iris(return_X_y=True)
>>> clf = OutputCodeClassifier(LinearSVC(dual="auto", random_state=0),
...                            code_size=2, random_state=0)
>>> clf.fit(X, y).predict(X)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1,
       1, 2, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 2, 2, 2, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 1, 1, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

1.12.2. Multilabel classification

Multilabel classification (closely related to multioutput classification) is a classification task labeling each sample with m labels from n_classes possible classes, where m can be 0 to n_classes inclusive. This can be thought of as predicting properties of a sample that are not mutually exclusive. Formally, a binary output is assigned to each class, for every sample. Positive classes are indicated with 1 and negative classes with 0 or -1. It is thus comparable to running n_classes binary classification tasks, for example with MultiOutputClassifier. This approach treats each label independently whereas multilabel classifiers may treat the multiple classes simultaneously, accounting for correlated behavior among them.

For example, prediction of the topics relevant to a text document or video. The document or video may be about one of ‘religion’, ‘politics’, ‘finance’ or ‘education’, several of the topic classes or all of the topic classes.

1.12.2.1. Target format

A valid representation of multilabel y is an either dense or sparse binary matrix of shape (n_samples, n_classes). Each column represents a class. The 1’s in each row denote the positive classes a sample has been labeled with. An example of a dense matrix y for 3 samples:

>>> y = np.array([[1, 0, 0, 1], [0, 0, 1, 1], [0, 0, 0, 0]])
>>> print(y)
[[1 0 0 1]
 [0 0 1 1]
 [0 0 0 0]]

Dense binary matrices can also be created using MultiLabelBinarizer. For more information, refer to Transforming the prediction target (y).

An example of the same y in sparse matrix form:

>>> y_sparse = sparse.csr_matrix(y)
>>> print(y_sparse)
  (0, 0)      1
  (0, 3)      1
  (1, 2)      1
  (1, 3)      1

1.12.2.2. MultiOutputClassifier

Multilabel classification support can be added to any classifier with MultiOutputClassifier. This strategy consists of fitting one classifier per target. This allows multiple target variable classifications. The purpose of this class is to extend estimators to be able to estimate a series of target functions (f1,f2,f3…,fn) that are trained on a single X predictor matrix to predict a series of responses (y1,y2,y3…,yn).

You can find a usage example for MultiOutputClassifier as part of the section on Multiclass-multioutput classification since it is a generalization of multilabel classification to multiclass outputs instead of binary outputs.

1.12.2.3. ClassifierChain

Classifier chains (see ClassifierChain) are a way of combining a number of binary classifiers into a single multi-label model that is capable of exploiting correlations among targets.

For a multi-label classification problem with N classes, N binary classifiers are assigned an integer between 0 and N-1. These integers define the order of models in the chain. Each classifier is then fit on the available training data plus the true labels of the classes whose models were assigned a lower number.

When predicting, the true labels will not be available. Instead the predictions of each model are passed on to the subsequent models in the chain to be used as features.

Clearly the order of the chain is important. The first model in the chain has no information about the other labels while the last model in the chain has features indicating the presence of all of the other labels. In general one does not know the optimal ordering of the models in the chain so typically many randomly ordered chains are fit and their predictions are averaged together.

1.12.3. Multiclass-multioutput classification

Multiclass-multioutput classification (also known as multitask classification) is a classification task which labels each sample with a set of non-binary properties. Both the number of properties and the number of classes per property is greater than 2. A single estimator thus handles several joint classification tasks. This is both a generalization of the multilabel classification task, which only considers binary attributes, as well as a generalization of the multiclass classification task, where only one property is considered.

For example, classification of the properties “type of fruit” and “colour” for a set of images of fruit. The property “type of fruit” has the possible classes: “apple”, “pear” and “orange”. The property “colour” has the possible classes: “green”, “red”, “yellow” and “orange”. Each sample is an image of a fruit, a label is output for both properties and each label is one of the possible classes of the corresponding property.

Note that all classifiers handling multiclass-multioutput (also known as multitask classification) tasks, support the multilabel classification task as a special case. Multitask classification is similar to the multioutput classification task with different model formulations. For more information, see the relevant estimator documentation.

Below is an example of multiclass-multioutput classification:

>>> from sklearn.datasets import make_classification
>>> from sklearn.multioutput import MultiOutputClassifier
>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.utils import shuffle
>>> import numpy as np
>>> X, y1 = make_classification(n_samples=10, n_features=100,
...                             n_informative=30, n_classes=3,
...                             random_state=1)
>>> y2 = shuffle(y1, random_state=1)
>>> y3 = shuffle(y1, random_state=2)
>>> Y = np.vstack((y1, y2, y3)).T
>>> n_samples, n_features = X.shape # 10,100
>>> n_outputs = Y.shape[1] # 3
>>> n_classes = 3
>>> forest = RandomForestClassifier(random_state=1)
>>> multi_target_forest = MultiOutputClassifier(forest, n_jobs=2)
>>> multi_target_forest.fit(X, Y).predict(X)
array([[2, 2, 0],
       [1, 2, 1],
       [2, 1, 0],
       [0, 0, 2],
       [0, 2, 1],
       [0, 0, 2],
       [1, 1, 0],
       [1, 1, 1],
       [0, 0, 2],
       [2, 0, 0]])

Warning

At present, no metric in sklearn.metrics supports the multiclass-multioutput classification task.

1.12.3.1. Target format

A valid representation of multioutput y is a dense matrix of shape (n_samples, n_classes) of class labels. A column wise concatenation of 1d multiclass variables. An example of y for 3 samples:

>>> y = np.array([['apple', 'green'], ['orange', 'orange'], ['pear', 'green']])
>>> print(y)
[['apple' 'green']
 ['orange' 'orange']
 ['pear' 'green']]

1.12.4. Multioutput regression

Multioutput regression predicts multiple numerical properties for each sample. Each property is a numerical variable and the number of properties to be predicted for each sample is greater than or equal to 2. Some estimators that support multioutput regression are faster than just running n_output estimators.

For example, prediction of both wind speed and wind direction, in degrees, using data obtained at a certain location. Each sample would be data obtained at one location and both wind speed and direction would be output for each sample.

1.12.4.1. Target format

A valid representation of multioutput y is a dense matrix of shape (n_samples, n_output) of floats. A column wise concatenation of continuous variables. An example of y for 3 samples:

>>> y = np.array([[31.4, 94], [40.5, 109], [25.0, 30]])
>>> print(y)
[[ 31.4  94. ]
 [ 40.5 109. ]
 [ 25.   30. ]]

1.12.4.2. MultiOutputRegressor

Multioutput regression support can be added to any regressor with MultiOutputRegressor. This strategy consists of fitting one regressor per target. Since each target is represented by exactly one regressor it is possible to gain knowledge about the target by inspecting its corresponding regressor. As MultiOutputRegressor fits one regressor per target it can not take advantage of correlations between targets.

Below is an example of multioutput regression:

>>> from sklearn.datasets import make_regression
>>> from sklearn.multioutput import MultiOutputRegressor
>>> from sklearn.ensemble import GradientBoostingRegressor
>>> X, y = make_regression(n_samples=10, n_targets=3, random_state=1)
>>> MultiOutputRegressor(GradientBoostingRegressor(random_state=0)).fit(X, y).predict(X)
array([[-154.75474165, -147.03498585,  -50.03812219],
       [   7.12165031,    5.12914884,  -81.46081961],
       [-187.8948621 , -100.44373091,   13.88978285],
       [-141.62745778,   95.02891072, -191.48204257],
       [  97.03260883,  165.34867495,  139.52003279],
       [ 123.92529176,   21.25719016,   -7.84253   ],
       [-122.25193977,  -85.16443186, -107.12274212],
       [ -30.170388  ,  -94.80956739,   12.16979946],
       [ 140.72667194,  176.50941682,  -17.50447799],
       [ 149.37967282,  -81.15699552,   -5.72850319]])

1.12.4.3. RegressorChain

Regressor chains (see RegressorChain) is analogous to ClassifierChain as a way of combining a number of regressions into a single multi-target model that is capable of exploiting correlations among targets.