Note
Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder
Linear Regression Example¶
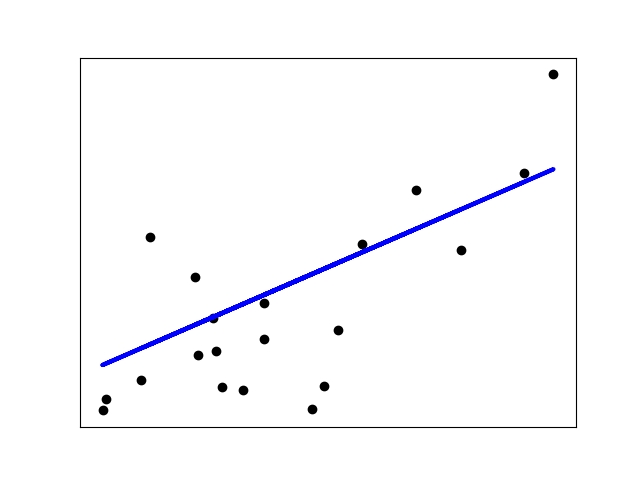
The example below uses only the first feature of the diabetes dataset,
in order to illustrate the data points within the two-dimensional plot.
The straight line can be seen in the plot, showing how linear regression
attempts to draw a straight line that will best minimize the
residual sum of squares between the observed responses in the dataset,
and the responses predicted by the linear approximation.
The coefficients, residual sum of squares and the coefficient of determination are also calculated.
Coefficients:
[938.23786125]
Mean squared error: 2548.07
Coefficient of determination: 0.47
# Code source: Jaques Grobler
# License: BSD 3 clause
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
# Load the diabetes dataset
diabetes_X, diabetes_y = datasets.load_diabetes(return_X_y=True)
# Use only one feature
diabetes_X = diabetes_X[:, np.newaxis, 2]
# Split the data into training/testing sets
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]
# Split the targets into training/testing sets
diabetes_y_train = diabetes_y[:-20]
diabetes_y_test = diabetes_y[-20:]
# Create linear regression object
regr = linear_model.LinearRegression()
# Train the model using the training sets
regr.fit(diabetes_X_train, diabetes_y_train)
# Make predictions using the testing set
diabetes_y_pred = regr.predict(diabetes_X_test)
# The coefficients
print("Coefficients: \n", regr.coef_)
# The mean squared error
print("Mean squared error: %.2f" % mean_squared_error(diabetes_y_test, diabetes_y_pred))
# The coefficient of determination: 1 is perfect prediction
print("Coefficient of determination: %.2f" % r2_score(diabetes_y_test, diabetes_y_pred))
# Plot outputs
plt.scatter(diabetes_X_test, diabetes_y_test, color="black")
plt.plot(diabetes_X_test, diabetes_y_pred, color="blue", linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()
Total running time of the script: (0 minutes 0.035 seconds)
Related examples
Ridge coefficients as a function of the L2 Regularization
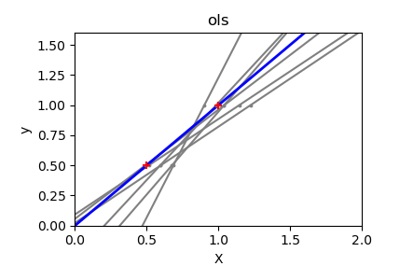
Ordinary Least Squares and Ridge Regression Variance
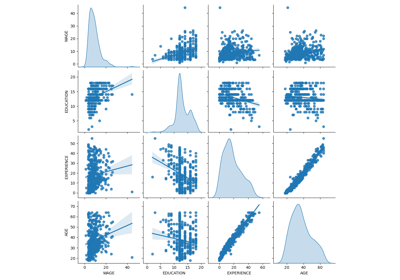
Common pitfalls in the interpretation of coefficients of linear models