`sklearn.manifold`.TSNE¶

class sklearn.manifold.TSNE(n_components=2, *, perplexity=30.0, early_exaggeration=12.0, learning_rate='auto', n_iter=1000, n_iter_without_progress=300, min_grad_norm=1e-07, metric='euclidean', metric_params=None, init='pca', verbose=0, random_state=None, method='barnes_hut', angle=0.5, n_jobs=None)[source]¶

T-distributed Stochastic Neighbor Embedding.

t-SNE [1] is a tool to visualize high-dimensional data. It converts similarities between data points to joint probabilities and tries to minimize the Kullback-Leibler divergence between the joint probabilities of the low-dimensional embedding and the high-dimensional data. t-SNE has a cost function that is not convex, i.e. with different initializations we can get different results.

It is highly recommended to use another dimensionality reduction method (e.g. PCA for dense data or TruncatedSVD for sparse data) to reduce the number of dimensions to a reasonable amount (e.g. 50) if the number of features is very high. This will suppress some noise and speed up the computation of pairwise distances between samples. For more tips see Laurens van der Maaten’s FAQ [2].

See also

sklearn.decomposition.PCA: Principal component analysis that is a linear dimensionality reduction method.
sklearn.decomposition.KernelPCA: Non-linear dimensionality reduction using kernels and PCA.
MDS: Manifold learning using multidimensional scaling.
Isomap: Manifold learning based on Isometric Mapping.
LocallyLinearEmbedding: Manifold learning using Locally Linear Embedding.
SpectralEmbedding: Spectral embedding for non-linear dimensionality.

References

[1] van der Maaten, L.J.P.; Hinton, G.E. Visualizing High-Dimensional Data: Using t-SNE. Journal of Machine Learning Research 9:2579-2605, 2008.
[2] van der Maaten, L.J.P. t-Distributed Stochastic Neighbor Embedding: https://lvdmaaten.github.io/tsne/
[3] L.J.P. van der Maaten. Accelerating t-SNE using Tree-Based Algorithms.: Journal of Machine Learning Research 15(Oct):3221-3245, 2014. https://lvdmaaten.github.io/publications/papers/JMLR_2014.pdf
[4] Belkina, A. C., Ciccolella, C. O., Anno, R., Halpert, R., Spidlen, J.,: & Snyder-Cappione, J. E. (2019). Automated optimized parameters for T-distributed stochastic neighbor embedding improve visualization and analysis of large datasets. Nature Communications, 10(1), 1-12.
[5] Kobak, D., & Berens, P. (2019). The art of using t-SNE for single-cell: transcriptomics. Nature Communications, 10(1), 1-14.

Examples

>>> import numpy as np
>>> from sklearn.manifold import TSNE
>>> X = np.array([[0, 0, 0], [0, 1, 1], [1, 0, 1], [1, 1, 1]])
>>> X_embedded = TSNE(n_components=2, learning_rate='auto',
...                   init='random', perplexity=3).fit_transform(X)
>>> X_embedded.shape
(4, 2)

Methods

`fit`(X[, y])	Fit X into an embedded space.
`fit_transform`(X[, y])	Fit X into an embedded space and return that transformed output.
`get_feature_names_out`([input_features])	Get output feature names for transformation.
`get_metadata_routing`()	Get metadata routing of this object.
`get_params`([deep])	Get parameters for this estimator.
`set_output`(*[, transform])	Set output container.
`set_params`(**params)	Set the parameters of this estimator.

fit(X, y=None)[source]¶

Fit X into an embedded space.

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features) or (n_samples, n_samples): If the metric is ‘precomputed’ X must be a square distance matrix. Otherwise it contains a sample per row. If the method is ‘exact’, X may be a sparse matrix of type ‘csr’, ‘csc’ or ‘coo’. If the method is ‘barnes_hut’ and the metric is ‘precomputed’, X may be a precomputed sparse graph.
yNone: Ignored.

Returns:

X_newarray of shape (n_samples, n_components): Embedding of the training data in low-dimensional space.

fit_transform(X, y=None)[source]¶

Fit X into an embedded space and return that transformed output.

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features) or (n_samples, n_samples): If the metric is ‘precomputed’ X must be a square distance matrix. Otherwise it contains a sample per row. If the method is ‘exact’, X may be a sparse matrix of type ‘csr’, ‘csc’ or ‘coo’. If the method is ‘barnes_hut’ and the metric is ‘precomputed’, X may be a precomputed sparse graph.
yNone: Ignored.

Returns:

X_newndarray of shape (n_samples, n_components): Embedding of the training data in low-dimensional space.

get_feature_names_out(input_features=None)[source]¶

Get output feature names for transformation.

The feature names out will prefixed by the lowercased class name. For example, if the transformer outputs 3 features, then the feature names out are: ["class_name0", "class_name1", "class_name2"].

Parameters:

input_featuresarray-like of str or None, default=None: Only used to validate feature names with the names seen in fit.

Returns:

feature_names_outndarray of str objects: Transformed feature names.

get_metadata_routing()[source]¶

Get metadata routing of this object.

Please check User Guide on how the routing mechanism works.

Returns:

routingMetadataRequest: A MetadataRequest encapsulating routing information.

get_params(deep=True)[source]¶

Get parameters for this estimator.

Parameters:

deepbool, default=True: If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

paramsdict: Parameter names mapped to their values.

set_output(*, transform=None)[source]¶

Set output container.

See Introducing the set_output API for an example on how to use the API.

Parameters:

transform{“default”, “pandas”}, default=None

Configure output of transform and fit_transform.

"default": Default output format of a transformer
"pandas": DataFrame output
None: Transform configuration is unchanged

Returns:

selfestimator instance: Estimator instance.

set_params(**params)[source]¶

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as Pipeline). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters:

**paramsdict: Estimator parameters.

Returns:

selfestimator instance: Estimator instance.

Examples using `sklearn.manifold.TSNE`¶

Comparison of Manifold Learning methods

Manifold Learning methods on a severed sphere

Manifold learning on handwritten digits: Locally Linear Embedding, Isomap…

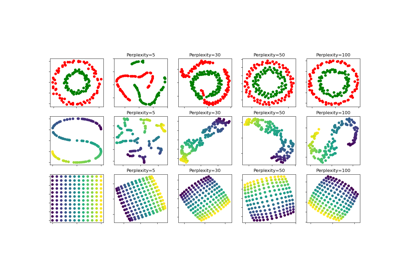
Manifold learning on handwritten digits: Locally Linear Embedding, Isomap...

Swiss Roll And Swiss-Hole Reduction

t-SNE: The effect of various perplexity values on the shape

Approximate nearest neighbors in TSNE

sklearn.manifold.TSNE¶

Examples using sklearn.manifold.TSNE¶

`sklearn.manifold`.TSNE¶

Examples using `sklearn.manifold.TSNE`¶