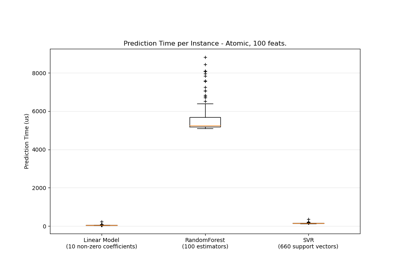
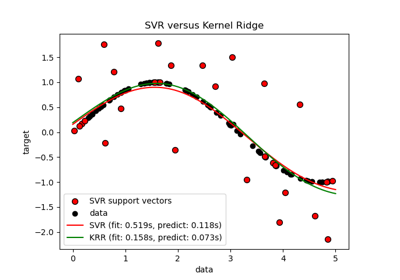
`sklearn.svm`.SVR¶

class sklearn.svm.SVR(*, kernel='rbf', degree=3, gamma='scale', coef0=0.0, tol=0.001, C=1.0, epsilon=0.1, shrinking=True, cache_size=200, verbose=False, max_iter=-1)[source]¶

Epsilon-Support Vector Regression.

The free parameters in the model are C and epsilon.

The implementation is based on libsvm. The fit time complexity is more than quadratic with the number of samples which makes it hard to scale to datasets with more than a couple of 10000 samples. For large datasets consider using LinearSVR or SGDRegressor instead, possibly after a Nystroem transformer or other Kernel Approximation.

See also

NuSVR: Support Vector Machine for regression implemented using libsvm using a parameter to control the number of support vectors.
LinearSVR: Scalable Linear Support Vector Machine for regression implemented using liblinear.

References

[1]

LIBSVM: A Library for Support Vector Machines

[2]

Platt, John (1999). “Probabilistic Outputs for Support Vector Machines and Comparisons to Regularized Likelihood Methods”

Examples

>>> from sklearn.svm import SVR
>>> from sklearn.pipeline import make_pipeline
>>> from sklearn.preprocessing import StandardScaler
>>> import numpy as np
>>> n_samples, n_features = 10, 5
>>> rng = np.random.RandomState(0)
>>> y = rng.randn(n_samples)
>>> X = rng.randn(n_samples, n_features)
>>> regr = make_pipeline(StandardScaler(), SVR(C=1.0, epsilon=0.2))
>>> regr.fit(X, y)
Pipeline(steps=[('standardscaler', StandardScaler()),
                ('svr', SVR(epsilon=0.2))])

Methods

`fit`(X, y[, sample_weight])	Fit the SVM model according to the given training data.
`get_params`([deep])	Get parameters for this estimator.
`predict`(X)	Perform regression on samples in X.
`score`(X, y[, sample_weight])	Return the coefficient of determination of the prediction.
`set_params`(**params)	Set the parameters of this estimator.

property coef_¶

Weights assigned to the features when kernel="linear".

Returns:

ndarray of shape (n_features, n_classes)

fit(X, y, sample_weight=None)[source]¶

Fit the SVM model according to the given training data.

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features) or (n_samples, n_samples): Training vectors, where n_samples is the number of samples and n_features is the number of features. For kernel=”precomputed”, the expected shape of X is (n_samples, n_samples).
yarray-like of shape (n_samples,): Target values (class labels in classification, real numbers in regression).
sample_weightarray-like of shape (n_samples,), default=None: Per-sample weights. Rescale C per sample. Higher weights force the classifier to put more emphasis on these points.

Returns:

selfobject: Fitted estimator.

Notes

If X and y are not C-ordered and contiguous arrays of np.float64 and X is not a scipy.sparse.csr_matrix, X and/or y may be copied.

If X is a dense array, then the other methods will not support sparse matrices as input.

get_params(deep=True)[source]¶

Get parameters for this estimator.

Parameters:

deepbool, default=True: If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

paramsdict: Parameter names mapped to their values.

property n_support_¶: Number of support vectors for each class.

predict(X)[source]¶

Perform regression on samples in X.

For an one-class model, +1 (inlier) or -1 (outlier) is returned.

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features): For kernel=”precomputed”, the expected shape of X is (n_samples_test, n_samples_train).

Returns:

y_predndarray of shape (n_samples,): The predicted values.

score(X, y, sample_weight=None)[source]¶

Return the coefficient of determination of the prediction.

The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares ((y_true - y_pred)** 2).sum() and \(v\) is the total sum of squares ((y_true - y_true.mean()) ** 2).sum(). The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of y, disregarding the input features, would get a \(R^2\) score of 0.0.

Parameters:

Xarray-like of shape (n_samples, n_features): Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape (n_samples, n_samples_fitted), where n_samples_fitted is the number of samples used in the fitting for the estimator.
yarray-like of shape (n_samples,) or (n_samples, n_outputs): True values for X.
sample_weightarray-like of shape (n_samples,), default=None: Sample weights.

Returns:

scorefloat: \(R^2\) of self.predict(X) w.r.t. y.

Notes

The \(R^2\) score used when calling score on a regressor uses multioutput='uniform_average' from version 0.23 to keep consistent with default value of r2_score. This influences the score method of all the multioutput regressors (except for MultiOutputRegressor).

set_params(**params)[source]¶

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as Pipeline). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters:

**paramsdict: Estimator parameters.

Returns:

selfestimator instance: Estimator instance.

Examples using `sklearn.svm.SVR`¶

Prediction Latency

Comparison of kernel ridge regression and SVR

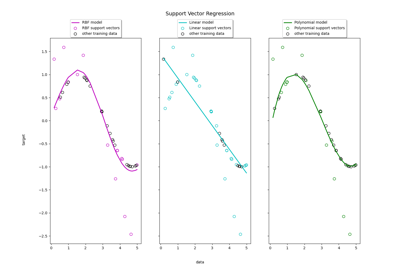
Support Vector Regression (SVR) using linear and non-linear kernels

sklearn.svm.SVR¶

Examples using sklearn.svm.SVR¶

`sklearn.svm`.SVR¶

Examples using `sklearn.svm.SVR`¶