sklearn.multioutput.MultiOutputRegressor

class sklearn.multioutput.MultiOutputRegressor(estimator, *, n_jobs=None)

Multi target regression.

This strategy consists of fitting one regressor per target. This is a simple strategy for extending regressors that do not natively support multi-target regression.

New in version 0.18.

Parameters:

estimatorestimator object

An estimator object implementing fit and predict.

n_jobsint or None, optional (default=None)

The number of jobs to run in parallel. fit, predict and partial_fit (if supported by the passed estimator) will be parallelized for each target.

When individual estimators are fast to train or predict, using n_jobs > 1 can result in slower performance due to the parallelism overhead.

None means 1 unless in a joblib.parallel_backend context. -1 means using all available processes / threads. See Glossary for more details.

Changed in version 0.20: n_jobs default changed from 1 to None.

Attributes:

estimators_list of n_output estimators

Estimators used for predictions.

n_features_in_int

Number of features seen during fit. Only defined if the underlying estimator exposes such an attribute when fit.

New in version 0.24.

feature_names_in_ndarray of shape (n_features_in_,)

Names of features seen during fit. Only defined if the underlying estimators expose such an attribute when fit.

New in version 1.0.

See also

RegressorChain

A multi-label model that arranges regressions into a chain.

MultiOutputClassifier

Classifies each output independently rather than chaining.

Examples

>>> import numpy as np
>>> from sklearn.datasets import load_linnerud
>>> from sklearn.multioutput import MultiOutputRegressor
>>> from sklearn.linear_model import Ridge
>>> X, y = load_linnerud(return_X_y=True)
>>> regr = MultiOutputRegressor(Ridge(random_state=123)).fit(X, y)
>>> regr.predict(X[[0]])
array([[176..., 35..., 57...]])

Methods

fit(X, y[, sample_weight])	Fit the model to data, separately for each output variable.
get_params([deep])	Get parameters for this estimator.
partial_fit(X, y[, sample_weight])	Incrementally fit the model to data, for each output variable.
predict(X)	Predict multi-output variable using model for each target variable.
score(X, y[, sample_weight])	Return the coefficient of determination of the prediction.
set_params(**params)	Set the parameters of this estimator.

fit(X, y, sample_weight=None, **fit_params)

Fit the model to data, separately for each output variable.

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features)

The input data.

y{array-like, sparse matrix} of shape (n_samples, n_outputs)

Multi-output targets. An indicator matrix turns on multilabel estimation.

sample_weightarray-like of shape (n_samples,), default=None

Sample weights. If None, then samples are equally weighted. Only supported if the underlying regressor supports sample weights.

**fit_paramsdict of string -> object

Parameters passed to the estimator.fit method of each step.

New in version 0.23.

Returns:

selfobject

Returns a fitted instance.

get_params(deep=True)

Get parameters for this estimator.

Parameters:

deepbool, default=True

If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

paramsdict

Parameter names mapped to their values.

partial_fit(X, y, sample_weight=None)

Incrementally fit the model to data, for each output variable.

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features)

The input data.

y{array-like, sparse matrix} of shape (n_samples, n_outputs)

Multi-output targets.

sample_weightarray-like of shape (n_samples,), default=None

Sample weights. If None, then samples are equally weighted. Only supported if the underlying regressor supports sample weights.

Returns:

selfobject

Returns a fitted instance.

predict(X)

Predict multi-output variable using model for each target variable.

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features)

The input data.

Returns:

y{array-like, sparse matrix} of shape (n_samples, n_outputs)

Multi-output targets predicted across multiple predictors. Note: Separate models are generated for each predictor.

score(X, y, sample_weight=None)

Return the coefficient of determination of the prediction.

The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares ((y_true - y_pred)** 2).sum() and \(v\) is the total sum of squares ((y_true - y_true.mean()) ** 2).sum(). The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of y, disregarding the input features, would get a \(R^2\) score of 0.0.

Parameters:

Xarray-like of shape (n_samples, n_features)

Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape (n_samples, n_samples_fitted), where n_samples_fitted is the number of samples used in the fitting for the estimator.

yarray-like of shape (n_samples,) or (n_samples, n_outputs)

True values for X.

sample_weightarray-like of shape (n_samples,), default=None

Sample weights.

Returns:

scorefloat

\(R^2\) of self.predict(X) w.r.t. y.

Notes

The \(R^2\) score used when calling score on a regressor uses multioutput='uniform_average' from version 0.23 to keep consistent with default value of r2_score. This influences the score method of all the multioutput regressors (except for MultiOutputRegressor).

set_params(**params)

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as Pipeline). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters:

**paramsdict

Estimator parameters.

Returns:

selfestimator instance

Estimator instance.

Examples using sklearn.multioutput.MultiOutputRegressor

Comparing random forests and the multi-output meta estimator

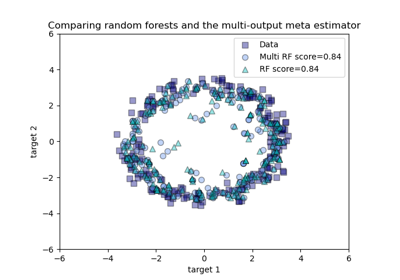
Comparing random forests and the multi-output meta estimator