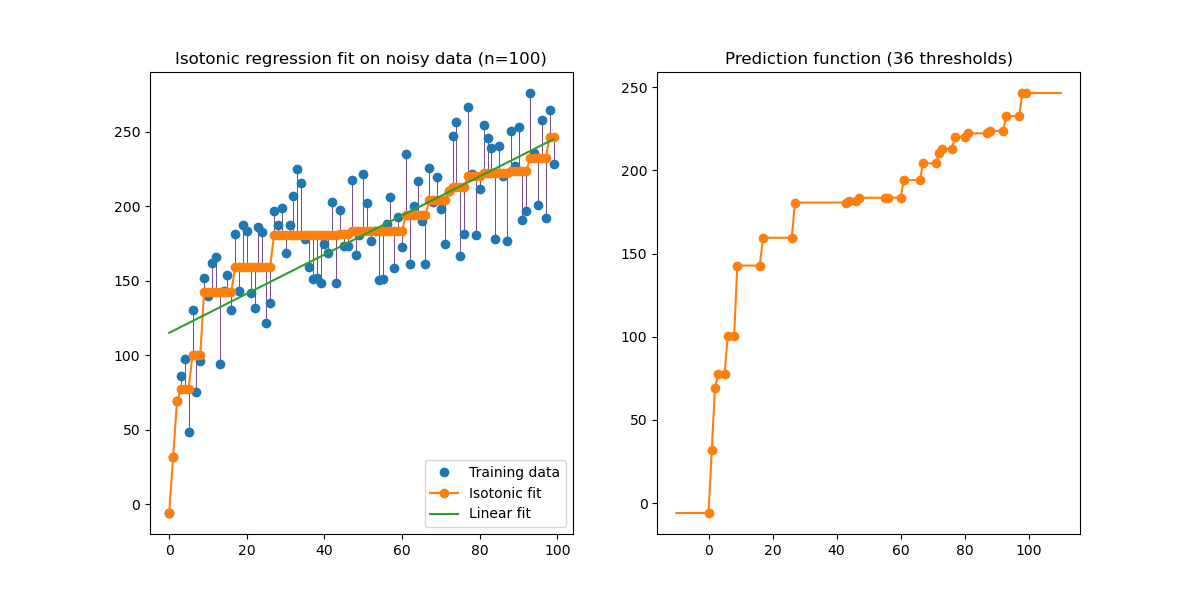
1.15. Isotonic regression¶
The class IsotonicRegression fits a non-decreasing real function to
1-dimensional data. It solves the following problem:
subject to \(\hat{y}_i \le \hat{y}_j\) whenever \(X_i \le X_j\),
where the weights \(w_i\) are strictly positive, and both X and y are
arbitrary real quantities.
The increasing parameter changes the constraint to
\(\hat{y}_i \ge \hat{y}_j\) whenever \(X_i \le X_j\). Setting it to
‘auto’ will automatically choose the constraint based on Spearman’s rank
correlation coefficient.
IsotonicRegression produces a series of predictions
\(\hat{y}_i\) for the training data which are the closest to the targets
\(y\) in terms of mean squared error. These predictions are interpolated
for predicting to unseen data. The predictions of IsotonicRegression
thus form a function that is piecewise linear: