8.2. Computational Performance

For some applications the performance (mainly latency and throughput at prediction time) of estimators is crucial. It may also be of interest to consider the training throughput but this is often less important in a production setup (where it often takes place offline).

We will review here the orders of magnitude you can expect from a number of scikit-learn estimators in different contexts and provide some tips and tricks for overcoming performance bottlenecks.

Prediction latency is measured as the elapsed time necessary to make a prediction (e.g. in micro-seconds). Latency is often viewed as a distribution and operations engineers often focus on the latency at a given percentile of this distribution (e.g. the 90 percentile).

Prediction throughput is defined as the number of predictions the software can deliver in a given amount of time (e.g. in predictions per second).

An important aspect of performance optimization is also that it can hurt prediction accuracy. Indeed, simpler models (e.g. linear instead of non-linear, or with fewer parameters) often run faster but are not always able to take into account the same exact properties of the data as more complex ones.

8.2.1. Prediction Latency

One of the most straight-forward concerns one may have when using/choosing a machine learning toolkit is the latency at which predictions can be made in a production environment.

The main factors that influence the prediction latency are

1. Number of features

2. Input data representation and sparsity

3. Model complexity

4. Feature extraction

A last major parameter is also the possibility to do predictions in bulk or one-at-a-time mode.

8.2.1.1. Bulk versus Atomic mode

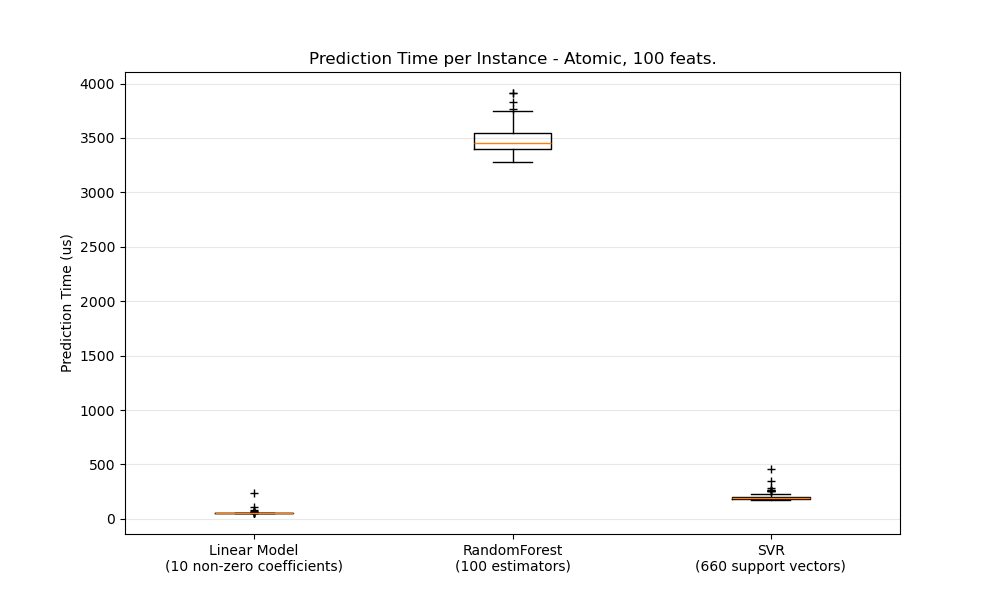
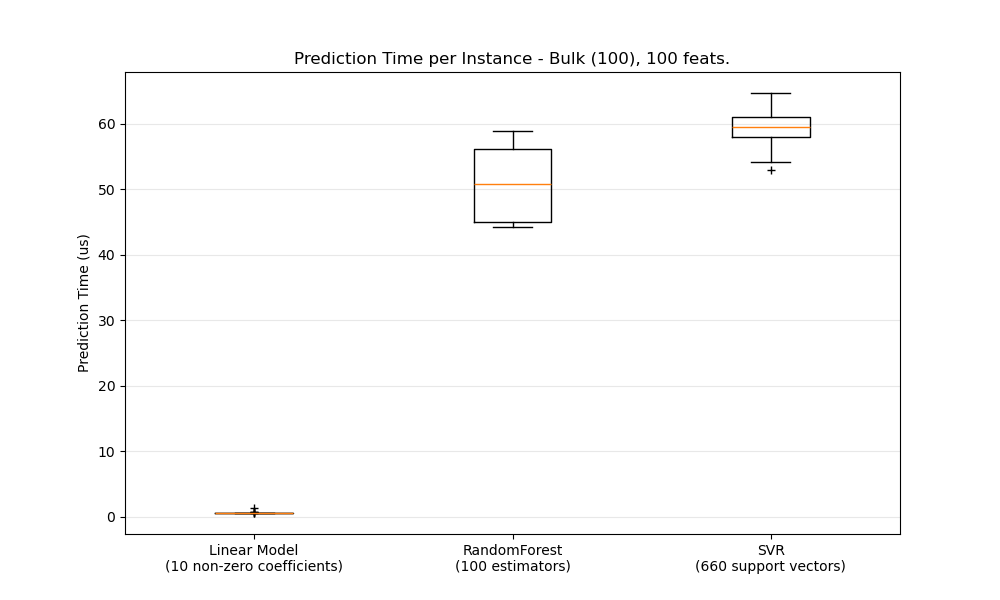
In general doing predictions in bulk (many instances at the same time) is more efficient for a number of reasons (branching predictability, CPU cache, linear algebra libraries optimizations etc.). Here we see on a setting with few features that independently of estimator choice the bulk mode is always faster, and for some of them by 1 to 2 orders of magnitude:

To benchmark different estimators for your case you can simply change the n_features parameter in this example: Prediction Latency. This should give you an estimate of the order of magnitude of the prediction latency.

8.2.1.2. Configuring Scikit-learn for reduced validation overhead

Scikit-learn does some validation on data that increases the overhead per call to predict and similar functions. In particular, checking that features are finite (not NaN or infinite) involves a full pass over the data. If you ensure that your data is acceptable, you may suppress checking for finiteness by setting the environment variable SKLEARN_ASSUME_FINITE to a non-empty string before importing scikit-learn, or configure it in Python with set_config. For more control than these global settings, a config_context allows you to set this configuration within a specified context:

>>> import sklearn
>>> with sklearn.config_context(assume_finite=True):
...     pass  # do learning/prediction here with reduced validation

Note that this will affect all uses of assert_all_finite within the context.

8.2.1.3. Influence of the Number of Features

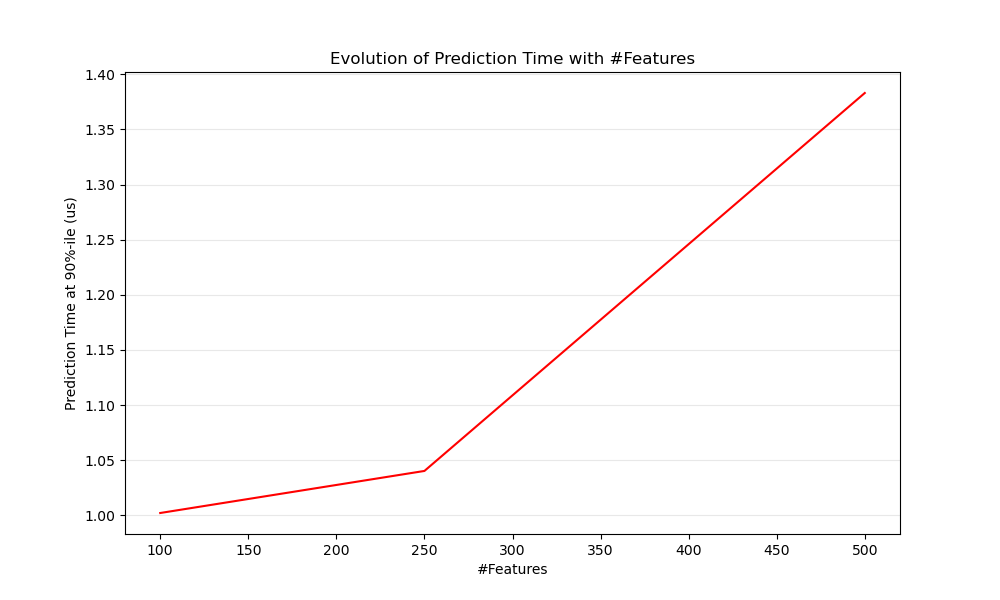
Obviously when the number of features increases so does the memory consumption of each example. Indeed, for a matrix of \(M\) instances with \(N\) features, the space complexity is in \(O(NM)\). From a computing perspective it also means that the number of basic operations (e.g., multiplications for vector-matrix products in linear models) increases too. Here is a graph of the evolution of the prediction latency with the number of features:

Overall you can expect the prediction time to increase at least linearly with the number of features (non-linear cases can happen depending on the global memory footprint and estimator).

8.2.1.4. Influence of the Input Data Representation

Scipy provides sparse matrix data structures which are optimized for storing sparse data. The main feature of sparse formats is that you don’t store zeros so if your data is sparse then you use much less memory. A non-zero value in a sparse (CSR or CSC) representation will only take on average one 32bit integer position + the 64 bit floating point value + an additional 32bit per row or column in the matrix. Using sparse input on a dense (or sparse) linear model can speedup prediction by quite a bit as only the non zero valued features impact the dot product and thus the model predictions. Hence if you have 100 non zeros in 1e6 dimensional space, you only need 100 multiply and add operation instead of 1e6.

Calculation over a dense representation, however, may leverage highly optimized vector operations and multithreading in BLAS, and tends to result in fewer CPU cache misses. So the sparsity should typically be quite high (10% non-zeros max, to be checked depending on the hardware) for the sparse input representation to be faster than the dense input representation on a machine with many CPUs and an optimized BLAS implementation.

Here is sample code to test the sparsity of your input:

def sparsity_ratio(X):
    return 1.0 - np.count_nonzero(X) / float(X.shape[0] * X.shape[1])
print("input sparsity ratio:", sparsity_ratio(X))

As a rule of thumb you can consider that if the sparsity ratio is greater than 90% you can probably benefit from sparse formats. Check Scipy’s sparse matrix formats documentation for more information on how to build (or convert your data to) sparse matrix formats. Most of the time the CSR and CSC formats work best.

8.2.1.5. Influence of the Model Complexity

Generally speaking, when model complexity increases, predictive power and latency are supposed to increase. Increasing predictive power is usually interesting, but for many applications we would better not increase prediction latency too much. We will now review this idea for different families of supervised models.

For sklearn.linear_model (e.g. Lasso, ElasticNet, SGDClassifier/Regressor, Ridge & RidgeClassifier, PassiveAggressiveClassifier/Regressor, LinearSVC, LogisticRegression…) the decision function that is applied at prediction time is the same (a dot product) , so latency should be equivalent.

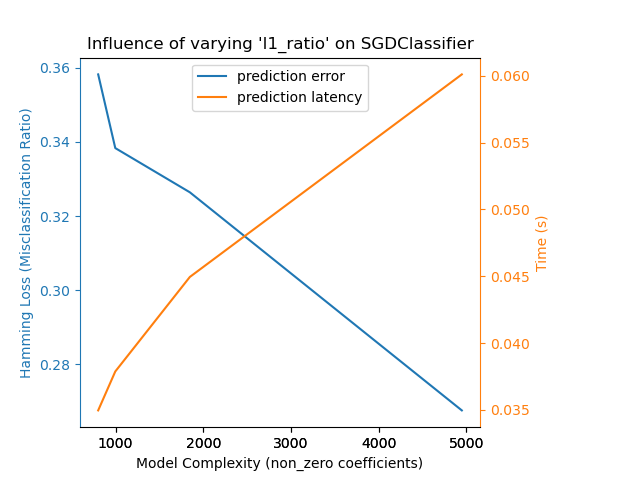
Here is an example using SGDClassifier with the elasticnet penalty. The regularization strength is globally controlled by the alpha parameter. With a sufficiently high alpha, one can then increase the l1_ratio parameter of elasticnet to enforce various levels of sparsity in the model coefficients. Higher sparsity here is interpreted as less model complexity as we need fewer coefficients to describe it fully. Of course sparsity influences in turn the prediction time as the sparse dot-product takes time roughly proportional to the number of non-zero coefficients.

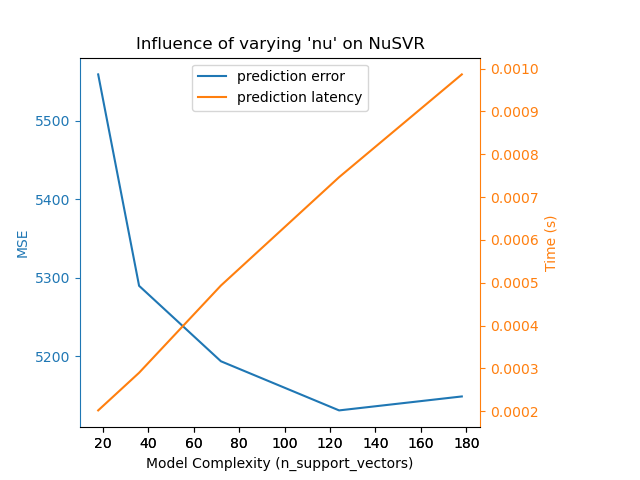
For the sklearn.svm family of algorithms with a non-linear kernel, the latency is tied to the number of support vectors (the fewer the faster). Latency and throughput should (asymptotically) grow linearly with the number of support vectors in a SVC or SVR model. The kernel will also influence the latency as it is used to compute the projection of the input vector once per support vector. In the following graph the nu parameter of NuSVR was used to influence the number of support vectors.

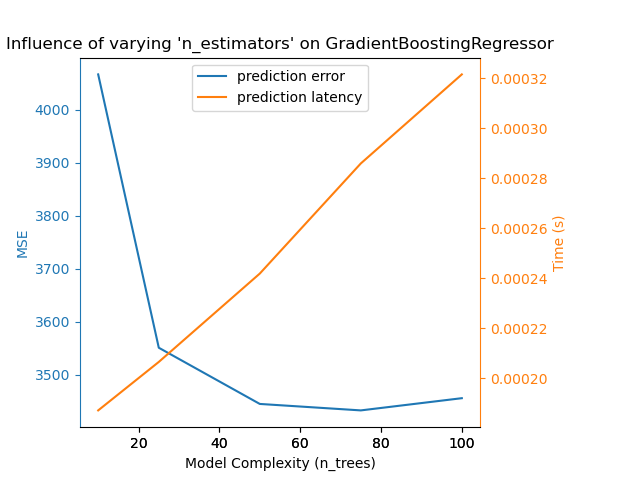
For sklearn.ensemble of trees (e.g. RandomForest, GBT, ExtraTrees, etc.) the number of trees and their depth play the most important role. Latency and throughput should scale linearly with the number of trees. In this case we used directly the n_estimators parameter of GradientBoostingRegressor.

In any case be warned that decreasing model complexity can hurt accuracy as mentioned above. For instance a non-linearly separable problem can be handled with a speedy linear model but prediction power will very likely suffer in the process.

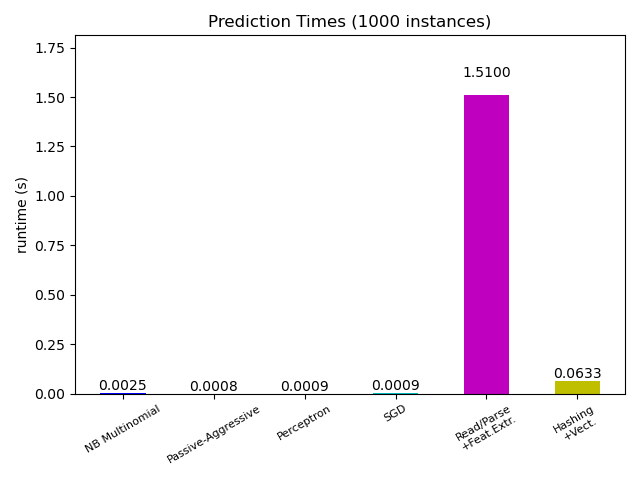
8.2.1.6. Feature Extraction Latency

Most scikit-learn models are usually pretty fast as they are implemented either with compiled Cython extensions or optimized computing libraries. On the other hand, in many real world applications the feature extraction process (i.e. turning raw data like database rows or network packets into numpy arrays) governs the overall prediction time. For example on the Reuters text classification task the whole preparation (reading and parsing SGML files, tokenizing the text and hashing it into a common vector space) is taking 100 to 500 times more time than the actual prediction code, depending on the chosen model.

In many cases it is thus recommended to carefully time and profile your feature extraction code as it may be a good place to start optimizing when your overall latency is too slow for your application.

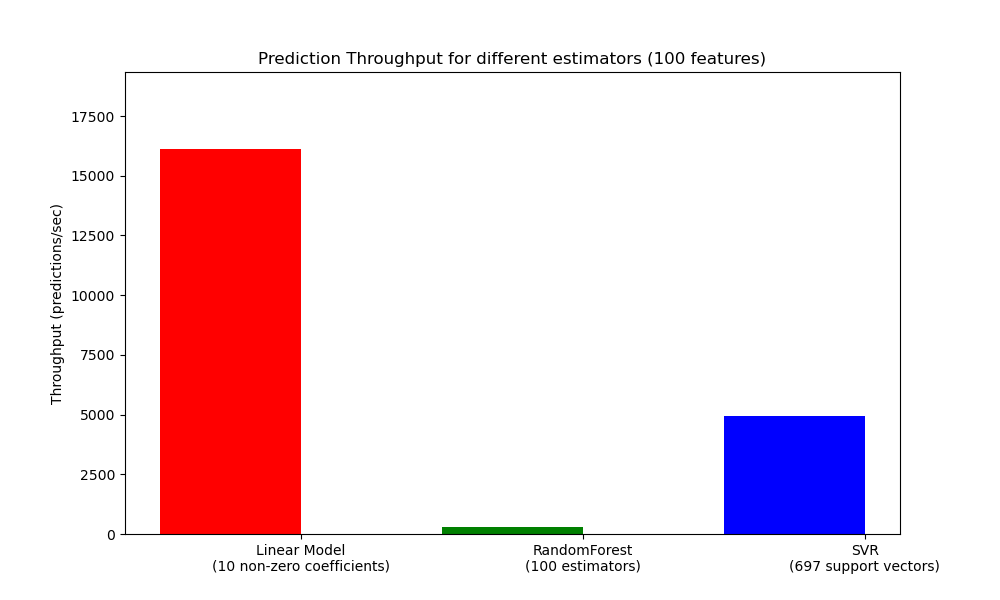
8.2.2. Prediction Throughput

Another important metric to care about when sizing production systems is the throughput i.e. the number of predictions you can make in a given amount of time. Here is a benchmark from the Prediction Latency example that measures this quantity for a number of estimators on synthetic data:

These throughputs are achieved on a single process. An obvious way to increase the throughput of your application is to spawn additional instances (usually processes in Python because of the GIL) that share the same model. One might also add machines to spread the load. A detailed explanation on how to achieve this is beyond the scope of this documentation though.

8.2.3. Tips and Tricks

8.2.3.1. Linear algebra libraries

As scikit-learn relies heavily on Numpy/Scipy and linear algebra in general it makes sense to take explicit care of the versions of these libraries. Basically, you ought to make sure that Numpy is built using an optimized BLAS / LAPACK library.

Not all models benefit from optimized BLAS and Lapack implementations. For instance models based on (randomized) decision trees typically do not rely on BLAS calls in their inner loops, nor do kernel SVMs (SVC, SVR, NuSVC, NuSVR). On the other hand a linear model implemented with a BLAS DGEMM call (via numpy.dot) will typically benefit hugely from a tuned BLAS implementation and lead to orders of magnitude speedup over a non-optimized BLAS.

You can display the BLAS / LAPACK implementation used by your NumPy / SciPy / scikit-learn install with the following command:

python -c "import sklearn; sklearn.show_versions()"

Optimized BLAS / LAPACK implementations include:

• Atlas (need hardware specific tuning by rebuilding on the target machine)

• OpenBLAS

• MKL

• Apple Accelerate and vecLib frameworks (OSX only)

More information can be found on the NumPy install page and in this blog post from Daniel Nouri which has some nice step by step install instructions for Debian / Ubuntu.

8.2.3.2. Limiting Working Memory

Some calculations when implemented using standard numpy vectorized operations involve using a large amount of temporary memory. This may potentially exhaust system memory. Where computations can be performed in fixed-memory chunks, we attempt to do so, and allow the user to hint at the maximum size of this working memory (defaulting to 1GB) using set_config or config_context. The following suggests to limit temporary working memory to 128 MiB:

>>> import sklearn
>>> with sklearn.config_context(working_memory=128):
...     pass  # do chunked work here

An example of a chunked operation adhering to this setting is pairwise_distances_chunked, which facilitates computing row-wise reductions of a pairwise distance matrix.

8.2.3.3. Model Compression

Model compression in scikit-learn only concerns linear models for the moment. In this context it means that we want to control the model sparsity (i.e. the number of non-zero coordinates in the model vectors). It is generally a good idea to combine model sparsity with sparse input data representation.

Here is sample code that illustrates the use of the sparsify() method:

clf = SGDRegressor(penalty='elasticnet', l1_ratio=0.25)
clf.fit(X_train, y_train).sparsify()
clf.predict(X_test)

In this example we prefer the elasticnet penalty as it is often a good compromise between model compactness and prediction power. One can also further tune the l1_ratio parameter (in combination with the regularization strength alpha) to control this tradeoff.

A typical benchmark on synthetic data yields a >30% decrease in latency when both the model and input are sparse (with 0.000024 and 0.027400 non-zero coefficients ratio respectively). Your mileage may vary depending on the sparsity and size of your data and model. Furthermore, sparsifying can be very useful to reduce the memory usage of predictive models deployed on production servers.

8.2.3.4. Model Reshaping

Model reshaping consists in selecting only a portion of the available features to fit a model. In other words, if a model discards features during the learning phase we can then strip those from the input. This has several benefits. Firstly it reduces memory (and therefore time) overhead of the model itself. It also allows to discard explicit feature selection components in a pipeline once we know which features to keep from a previous run. Finally, it can help reduce processing time and I/O usage upstream in the data access and feature extraction layers by not collecting and building features that are discarded by the model. For instance if the raw data come from a database, it can make it possible to write simpler and faster queries or reduce I/O usage by making the queries return lighter records. At the moment, reshaping needs to be performed manually in scikit-learn. In the case of sparse input (particularly in CSR format), it is generally sufficient to not generate the relevant features, leaving their columns empty.

8.2.3.5. Links

• scikit-learn developer performance documentation

• Scipy sparse matrix formats documentation