Note
Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder
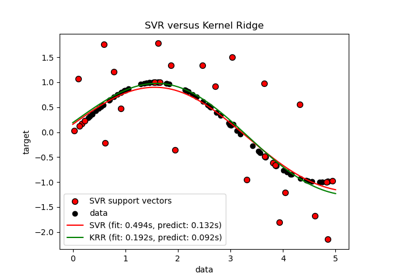
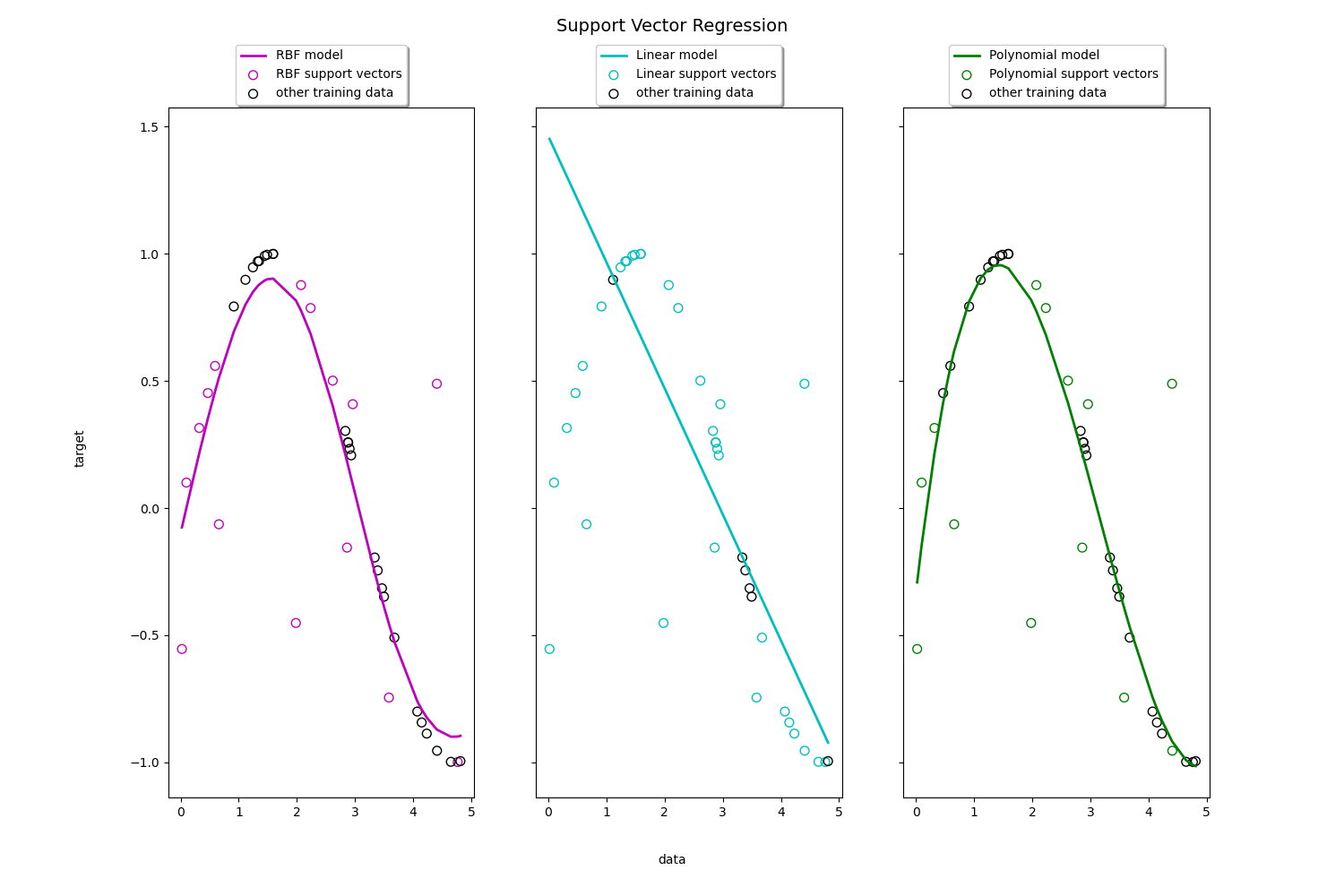
Support Vector Regression (SVR) using linear and non-linear kernels¶
Toy example of 1D regression using linear, polynomial and RBF kernels.
import matplotlib.pyplot as plt
import numpy as np
from sklearn.svm import SVR
Generate sample data¶
X = np.sort(5 * np.random.rand(40, 1), axis=0)
y = np.sin(X).ravel()
# add noise to targets
y[::5] += 3 * (0.5 - np.random.rand(8))
Fit regression model¶
Look at the results¶
lw = 2
svrs = [svr_rbf, svr_lin, svr_poly]
kernel_label = ["RBF", "Linear", "Polynomial"]
model_color = ["m", "c", "g"]
fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(15, 10), sharey=True)
for ix, svr in enumerate(svrs):
axes[ix].plot(
X,
svr.fit(X, y).predict(X),
color=model_color[ix],
lw=lw,
label="{} model".format(kernel_label[ix]),
)
axes[ix].scatter(
X[svr.support_],
y[svr.support_],
facecolor="none",
edgecolor=model_color[ix],
s=50,
label="{} support vectors".format(kernel_label[ix]),
)
axes[ix].scatter(
X[np.setdiff1d(np.arange(len(X)), svr.support_)],
y[np.setdiff1d(np.arange(len(X)), svr.support_)],
facecolor="none",
edgecolor="k",
s=50,
label="other training data",
)
axes[ix].legend(
loc="upper center",
bbox_to_anchor=(0.5, 1.1),
ncol=1,
fancybox=True,
shadow=True,
)
fig.text(0.5, 0.04, "data", ha="center", va="center")
fig.text(0.06, 0.5, "target", ha="center", va="center", rotation="vertical")
fig.suptitle("Support Vector Regression", fontsize=14)
plt.show()
Total running time of the script: (0 minutes 0.400 seconds)
Related examples
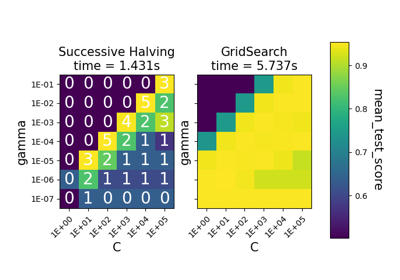
Comparison between grid search and successive halving
Comparison between grid search and successive halving