`sklearn.compose`.TransformedTargetRegressor¶

class sklearn.compose.TransformedTargetRegressor(regressor=None, *, transformer=None, func=None, inverse_func=None, check_inverse=True)[source]¶

Meta-estimator to regress on a transformed target.

Useful for applying a non-linear transformation to the target y in regression problems. This transformation can be given as a Transformer such as the QuantileTransformer or as a function and its inverse such as np.log and np.exp.

The computation during fit is:

regressor.fit(X, func(y))

or:

regressor.fit(X, transformer.transform(y))

The computation during predict is:

inverse_func(regressor.predict(X))

or:

transformer.inverse_transform(regressor.predict(X))

See also

sklearn.preprocessing.FunctionTransformer: Construct a transformer from an arbitrary callable.

Notes

Internally, the target y is always converted into a 2-dimensional array to be used by scikit-learn transformers. At the time of prediction, the output will be reshaped to a have the same number of dimensions as y.

Examples

>>> import numpy as np
>>> from sklearn.linear_model import LinearRegression
>>> from sklearn.compose import TransformedTargetRegressor
>>> tt = TransformedTargetRegressor(regressor=LinearRegression(),
...                                 func=np.log, inverse_func=np.exp)
>>> X = np.arange(4).reshape(-1, 1)
>>> y = np.exp(2 * X).ravel()
>>> tt.fit(X, y)
TransformedTargetRegressor(...)
>>> tt.score(X, y)
1.0
>>> tt.regressor_.coef_
array([2.])

For a more detailed example use case refer to Effect of transforming the targets in regression model.

Methods

`fit`(X, y, **fit_params)	Fit the model according to the given training data.
`get_metadata_routing`()	Get metadata routing of this object.
`get_params`([deep])	Get parameters for this estimator.
`predict`(X, **predict_params)	Predict using the base regressor, applying inverse.
`score`(X, y[, sample_weight])	Return the coefficient of determination of the prediction.
`set_params`(**params)	Set the parameters of this estimator.
`set_score_request`(*[, sample_weight])	Request metadata passed to the `score` method.

fit(X, y, **fit_params)[source]¶

Fit the model according to the given training data.

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features): Training vector, where n_samples is the number of samples and n_features is the number of features.
yarray-like of shape (n_samples,): Target values.
**fit_paramsdict: Parameters passed to the fit method of the underlying regressor.

Returns:

selfobject: Fitted estimator.

get_metadata_routing()[source]¶

Get metadata routing of this object.

Please check User Guide on how the routing mechanism works.

Returns:

routingMetadataRequest: A MetadataRequest encapsulating routing information.

get_params(deep=True)[source]¶

Get parameters for this estimator.

Parameters:

deepbool, default=True: If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

paramsdict: Parameter names mapped to their values.

property n_features_in_¶: Number of features seen during fit.

predict(X, **predict_params)[source]¶

Predict using the base regressor, applying inverse.

The regressor is used to predict and the inverse_func or inverse_transform is applied before returning the prediction.

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features): Samples.
**predict_paramsdict of str -> object: Parameters passed to the predict method of the underlying regressor.

Returns:

y_hatndarray of shape (n_samples,): Predicted values.

score(X, y, sample_weight=None)[source]¶

Return the coefficient of determination of the prediction.

The coefficient of determination $R^2$ is defined as $(1 - \frac{u}{v})$, where $u$ is the residual sum of squares ((y_true - y_pred)** 2).sum() and $v$ is the total sum of squares ((y_true - y_true.mean()) ** 2).sum(). The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of y, disregarding the input features, would get a $R^2$ score of 0.0.

Parameters:

Xarray-like of shape (n_samples, n_features): Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape (n_samples, n_samples_fitted), where n_samples_fitted is the number of samples used in the fitting for the estimator.
yarray-like of shape (n_samples,) or (n_samples, n_outputs): True values for X.
sample_weightarray-like of shape (n_samples,), default=None: Sample weights.

Returns:

scorefloat: $R^2$ of self.predict(X) w.r.t. y.

Notes

The $R^2$ score used when calling score on a regressor uses multioutput='uniform_average' from version 0.23 to keep consistent with default value of r2_score. This influences the score method of all the multioutput regressors (except for MultiOutputRegressor).

set_params(**params)[source]¶

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as Pipeline). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters:

**paramsdict: Estimator parameters.

Returns:

selfestimator instance: Estimator instance.

set_score_request(*, sample_weight: Union[bool, None, str] = '$UNCHANGED$') → TransformedTargetRegressor[source]¶

Request metadata passed to the score method.

Note that this method is only relevant if enable_metadata_routing=True (see sklearn.set_config). Please see User Guide on how the routing mechanism works.

The options for each parameter are:

True: metadata is requested, and passed to score if provided. The request is ignored if metadata is not provided.
False: metadata is not requested and the meta-estimator will not pass it to score.
None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.
str: metadata should be passed to the meta-estimator with this given alias instead of the original name.

The default (sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.

New in version 1.3.

Note

This method is only relevant if this estimator is used as a sub-estimator of a meta-estimator, e.g. used inside a Pipeline. Otherwise it has no effect.

Parameters:

sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED: Metadata routing for sample_weight parameter in score.

Returns:

selfobject: The updated object.

Examples using `sklearn.compose.TransformedTargetRegressor`¶

Poisson regression and non-normal loss

Common pitfalls in the interpretation of coefficients of linear models

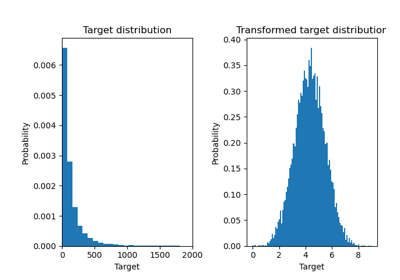
Effect of transforming the targets in regression model

sklearn.compose.TransformedTargetRegressor¶

Examples using sklearn.compose.TransformedTargetRegressor¶

`sklearn.compose`.TransformedTargetRegressor¶

Examples using `sklearn.compose.TransformedTargetRegressor`¶