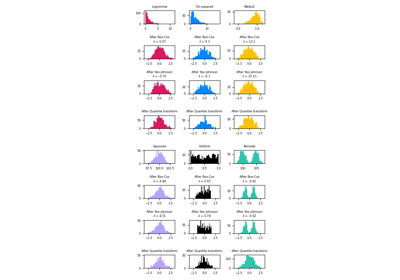
`sklearn.preprocessing`.QuantileTransformer¶

class sklearn.preprocessing.QuantileTransformer(*, n_quantiles=1000, output_distribution='uniform', ignore_implicit_zeros=False, subsample=10000, random_state=None, copy=True)[source]¶

Transform features using quantiles information.

This method transforms the features to follow a uniform or a normal distribution. Therefore, for a given feature, this transformation tends to spread out the most frequent values. It also reduces the impact of (marginal) outliers: this is therefore a robust preprocessing scheme.

The transformation is applied on each feature independently. First an estimate of the cumulative distribution function of a feature is used to map the original values to a uniform distribution. The obtained values are then mapped to the desired output distribution using the associated quantile function. Features values of new/unseen data that fall below or above the fitted range will be mapped to the bounds of the output distribution. Note that this transform is non-linear. It may distort linear correlations between variables measured at the same scale but renders variables measured at different scales more directly comparable.

See also

quantile_transform: Equivalent function without the estimator API.
PowerTransformer: Perform mapping to a normal distribution using a power transform.
StandardScaler: Perform standardization that is faster, but less robust to outliers.
RobustScaler: Perform robust standardization that removes the influence of outliers but does not put outliers and inliers on the same scale.

Notes

NaNs are treated as missing values: disregarded in fit, and maintained in transform.

For a comparison of the different scalers, transformers, and normalizers, see examples/preprocessing/plot_all_scaling.py.

Examples

>>> import numpy as np
>>> from sklearn.preprocessing import QuantileTransformer
>>> rng = np.random.RandomState(0)
>>> X = np.sort(rng.normal(loc=0.5, scale=0.25, size=(25, 1)), axis=0)
>>> qt = QuantileTransformer(n_quantiles=10, random_state=0)
>>> qt.fit_transform(X)
array([...])

Methods

`fit`(X[, y])	Compute the quantiles used for transforming.
`fit_transform`(X[, y])	Fit to data, then transform it.
`get_feature_names_out`([input_features])	Get output feature names for transformation.
`get_params`([deep])	Get parameters for this estimator.
`inverse_transform`(X)	Back-projection to the original space.
`set_output`(*[, transform])	Set output container.
`set_params`(**params)	Set the parameters of this estimator.
`transform`(X)	Feature-wise transformation of the data.

fit(X, y=None)[source]¶

Compute the quantiles used for transforming.

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features): The data used to scale along the features axis. If a sparse matrix is provided, it will be converted into a sparse csc_matrix. Additionally, the sparse matrix needs to be nonnegative if ignore_implicit_zeros is False.
yNone: Ignored.

Returns:

selfobject: Fitted transformer.

fit_transform(X, y=None, **fit_params)[source]¶

Fit to data, then transform it.

Fits transformer to X and y with optional parameters fit_params and returns a transformed version of X.

Parameters:

Xarray-like of shape (n_samples, n_features): Input samples.
yarray-like of shape (n_samples,) or (n_samples, n_outputs), default=None: Target values (None for unsupervised transformations).
**fit_paramsdict: Additional fit parameters.

Returns:

X_newndarray array of shape (n_samples, n_features_new): Transformed array.

get_feature_names_out(input_features=None)[source]¶

Get output feature names for transformation.

Parameters:

input_featuresarray-like of str or None, default=None

Input features.

If input_features is None, then feature_names_in_ is used as feature names in. If feature_names_in_ is not defined, then the following input feature names are generated: ["x0", "x1", ..., "x(n_features_in_ - 1)"].
If input_features is an array-like, then input_features must match feature_names_in_ if feature_names_in_ is defined.

Returns:

feature_names_outndarray of str objects: Same as input features.

get_params(deep=True)[source]¶

Get parameters for this estimator.

Parameters:

deepbool, default=True: If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

paramsdict: Parameter names mapped to their values.

inverse_transform(X)[source]¶

Back-projection to the original space.

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features): The data used to scale along the features axis. If a sparse matrix is provided, it will be converted into a sparse csc_matrix. Additionally, the sparse matrix needs to be nonnegative if ignore_implicit_zeros is False.

Returns:

Xt{ndarray, sparse matrix} of (n_samples, n_features): The projected data.

set_output(*, transform=None)[source]¶

Set output container.

See Introducing the set_output API for an example on how to use the API.

Parameters:

transform{“default”, “pandas”}, default=None

Configure output of transform and fit_transform.

"default": Default output format of a transformer
"pandas": DataFrame output
None: Transform configuration is unchanged

Returns:

selfestimator instance: Estimator instance.

set_params(**params)[source]¶

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as Pipeline). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters:

**paramsdict: Estimator parameters.

Returns:

selfestimator instance: Estimator instance.

transform(X)[source]¶

Feature-wise transformation of the data.

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features): The data used to scale along the features axis. If a sparse matrix is provided, it will be converted into a sparse csc_matrix. Additionally, the sparse matrix needs to be nonnegative if ignore_implicit_zeros is False.

Returns:

Xt{ndarray, sparse matrix} of shape (n_samples, n_features): The projected data.

Examples using `sklearn.preprocessing.QuantileTransformer`¶

Partial Dependence and Individual Conditional Expectation Plots

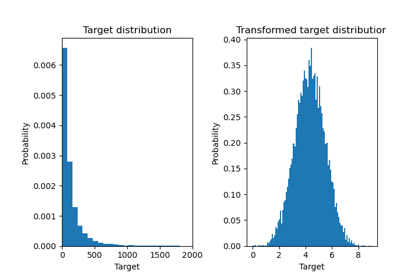
Effect of transforming the targets in regression model

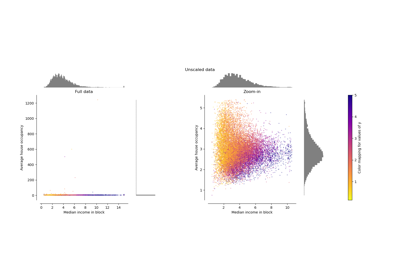
Compare the effect of different scalers on data with outliers

Map data to a normal distribution

sklearn.preprocessing.QuantileTransformer¶

Examples using sklearn.preprocessing.QuantileTransformer¶

`sklearn.preprocessing`.QuantileTransformer¶

Examples using `sklearn.preprocessing.QuantileTransformer`¶