`sklearn.linear_model`.RidgeCV¶

class sklearn.linear_model.RidgeCV(alphas=(0.1, 1.0, 10.0), *, fit_intercept=True, scoring=None, cv=None, gcv_mode=None, store_cv_values=False, alpha_per_target=False)[source]¶

Ridge regression with built-in cross-validation.

See glossary entry for cross-validation estimator.

By default, it performs efficient Leave-One-Out Cross-Validation.

Read more in the User Guide.

Parameters:

alphasarray-like of shape (n_alphas,), default=(0.1, 1.0, 10.0)

Array of alpha values to try. Regularization strength; must be a positive float. Regularization improves the conditioning of the problem and reduces the variance of the estimates. Larger values specify stronger regularization. Alpha corresponds to 1 / (2C) in other linear models such as LogisticRegression or LinearSVC. If using Leave-One-Out cross-validation, alphas must be positive.

fit_interceptbool, default=True

Whether to calculate the intercept for this model. If set to false, no intercept will be used in calculations (i.e. data is expected to be centered).

scoringstr, callable, default=None

A string (see model evaluation documentation) or a scorer callable object / function with signature scorer(estimator, X, y). If None, the negative mean squared error if cv is ‘auto’ or None (i.e. when using leave-one-out cross-validation), and r2 score otherwise.

cvint, cross-validation generator or an iterable, default=None

Determines the cross-validation splitting strategy. Possible inputs for cv are:

None, to use the efficient Leave-One-Out cross-validation
integer, to specify the number of folds.
CV splitter,
An iterable yielding (train, test) splits as arrays of indices.

For integer/None inputs, if y is binary or multiclass, StratifiedKFold is used, else, KFold is used.

Refer User Guide for the various cross-validation strategies that can be used here.

gcv_mode{‘auto’, ‘svd’, ‘eigen’}, default=’auto’

Flag indicating which strategy to use when performing Leave-One-Out Cross-Validation. Options are:

'auto' : use 'svd' if n_samples > n_features, otherwise use 'eigen'
'svd' : force use of singular value decomposition of X when X is
    dense, eigenvalue decomposition of X^T.X when X is sparse.
'eigen' : force computation via eigendecomposition of X.X^T

The ‘auto’ mode is the default and is intended to pick the cheaper option of the two depending on the shape of the training data.

store_cv_valuesbool, default=False

Flag indicating if the cross-validation values corresponding to each alpha should be stored in the cv_values_ attribute (see below). This flag is only compatible with cv=None (i.e. using Leave-One-Out Cross-Validation).

alpha_per_targetbool, default=False

Flag indicating whether to optimize the alpha value (picked from the alphas parameter list) for each target separately (for multi-output settings: multiple prediction targets). When set to True, after fitting, the alpha_ attribute will contain a value for each target. When set to False, a single alpha is used for all targets.

New in version 0.24.

Attributes:

cv_values_ndarray of shape (n_samples, n_alphas) or shape (n_samples, n_targets, n_alphas), optional: Cross-validation values for each alpha (only available if store_cv_values=True and cv=None). After fit() has been called, this attribute will contain the mean squared errors if scoring is None otherwise it will contain standardized per point prediction values.
coef_ndarray of shape (n_features) or (n_targets, n_features): Weight vector(s).
intercept_float or ndarray of shape (n_targets,): Independent term in decision function. Set to 0.0 if fit_intercept = False.
alpha_float or ndarray of shape (n_targets,): Estimated regularization parameter, or, if alpha_per_target=True, the estimated regularization parameter for each target.
best_score_float or ndarray of shape (n_targets,): Score of base estimator with best alpha, or, if alpha_per_target=True, a score for each target.

New in version 0.23.
n_features_in_int: Number of features seen during fit.

New in version 0.24.
feature_names_in_ndarray of shape (n_features_in_,): Names of features seen during fit. Defined only when X has feature names that are all strings.

New in version 1.0.

See also

Ridge: Ridge regression.
RidgeClassifier: Classifier based on ridge regression on {-1, 1} labels.
RidgeClassifierCV: Ridge classifier with built-in cross validation.

Examples

>>> from sklearn.datasets import load_diabetes
>>> from sklearn.linear_model import RidgeCV
>>> X, y = load_diabetes(return_X_y=True)
>>> clf = RidgeCV(alphas=[1e-3, 1e-2, 1e-1, 1]).fit(X, y)
>>> clf.score(X, y)
0.5166...

Methods

`fit`(X, y[, sample_weight])	Fit Ridge regression model with cv.
`get_params`([deep])	Get parameters for this estimator.
`predict`(X)	Predict using the linear model.
`score`(X, y[, sample_weight])	Return the coefficient of determination of the prediction.
`set_params`(**params)	Set the parameters of this estimator.

fit(X, y, sample_weight=None)[source]¶

Fit Ridge regression model with cv.

Parameters:

Xndarray of shape (n_samples, n_features): Training data. If using GCV, will be cast to float64 if necessary.
yndarray of shape (n_samples,) or (n_samples, n_targets): Target values. Will be cast to X’s dtype if necessary.
sample_weightfloat or ndarray of shape (n_samples,), default=None: Individual weights for each sample. If given a float, every sample will have the same weight.

Returns:

selfobject: Fitted estimator.

Notes

When sample_weight is provided, the selected hyperparameter may depend on whether we use leave-one-out cross-validation (cv=None or cv=’auto’) or another form of cross-validation, because only leave-one-out cross-validation takes the sample weights into account when computing the validation score.

get_params(deep=True)[source]¶

Get parameters for this estimator.

Parameters:

deepbool, default=True: If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

paramsdict: Parameter names mapped to their values.

predict(X)[source]¶

Predict using the linear model.

Parameters:

Xarray-like or sparse matrix, shape (n_samples, n_features): Samples.

Returns:

Carray, shape (n_samples,): Returns predicted values.

score(X, y, sample_weight=None)[source]¶

Return the coefficient of determination of the prediction.

The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares ((y_true - y_pred)** 2).sum() and \(v\) is the total sum of squares ((y_true - y_true.mean()) ** 2).sum(). The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of y, disregarding the input features, would get a \(R^2\) score of 0.0.

Parameters:

Xarray-like of shape (n_samples, n_features): Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape (n_samples, n_samples_fitted), where n_samples_fitted is the number of samples used in the fitting for the estimator.
yarray-like of shape (n_samples,) or (n_samples, n_outputs): True values for X.
sample_weightarray-like of shape (n_samples,), default=None: Sample weights.

Returns:

scorefloat: \(R^2\) of self.predict(X) w.r.t. y.

Notes

The \(R^2\) score used when calling score on a regressor uses multioutput='uniform_average' from version 0.23 to keep consistent with default value of r2_score. This influences the score method of all the multioutput regressors (except for MultiOutputRegressor).

set_params(**params)[source]¶

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as Pipeline). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters:

**paramsdict: Estimator parameters.

Returns:

selfestimator instance: Estimator instance.

Examples using `sklearn.linear_model.RidgeCV`¶

Combine predictors using stacking

Time-related feature engineering

Model-based and sequential feature selection

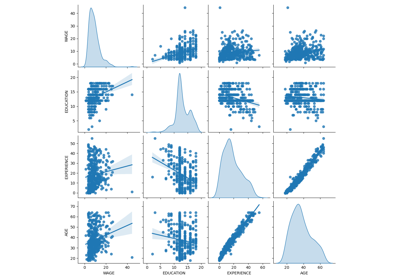
Common pitfalls in the interpretation of coefficients of linear models

Face completion with a multi-output estimators

Effect of transforming the targets in regression model

sklearn.linear_model.RidgeCV¶

Examples using sklearn.linear_model.RidgeCV¶

`sklearn.linear_model`.RidgeCV¶

Examples using `sklearn.linear_model.RidgeCV`¶