sklearn.random_projection.SparseRandomProjection¶

class sklearn.random_projection.SparseRandomProjection(n_components='auto', *, density='auto', eps=0.1, dense_output=False, random_state=None)[source]¶

Reduce dimensionality through sparse random projection.

Sparse random matrix is an alternative to dense random projection matrix that guarantees similar embedding quality while being much more memory efficient and allowing faster computation of the projected data.

If we note s = 1 / density the components of the random matrix are drawn from:

• -sqrt(s) / sqrt(n_components) with probability 1 / 2s

• 0 with probability 1 - 1 / s

• +sqrt(s) / sqrt(n_components) with probability 1 / 2s

Read more in the User Guide.

New in version 0.13.

Parameters

n_componentsint or ‘auto’, default=’auto’

Dimensionality of the target projection space.

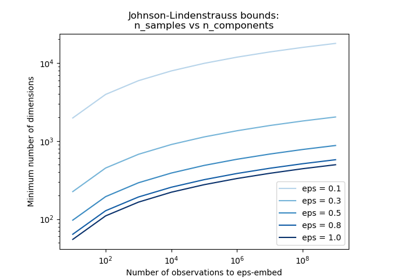
n_components can be automatically adjusted according to the number of samples in the dataset and the bound given by the Johnson-Lindenstrauss lemma. In that case the quality of the embedding is controlled by the eps parameter.

It should be noted that Johnson-Lindenstrauss lemma can yield very conservative estimated of the required number of components as it makes no assumption on the structure of the dataset.

densityfloat or ‘auto’, default=’auto’

Ratio in the range (0, 1] of non-zero component in the random projection matrix.

If density = ‘auto’, the value is set to the minimum density as recommended by Ping Li et al.: 1 / sqrt(n_features).

Use density = 1 / 3.0 if you want to reproduce the results from Achlioptas, 2001.

epsfloat, default=0.1

Parameter to control the quality of the embedding according to the Johnson-Lindenstrauss lemma when n_components is set to ‘auto’. This value should be strictly positive.

Smaller values lead to better embedding and higher number of dimensions (n_components) in the target projection space.

dense_outputbool, default=False

If True, ensure that the output of the random projection is a dense numpy array even if the input and random projection matrix are both sparse. In practice, if the number of components is small the number of zero components in the projected data will be very small and it will be more CPU and memory efficient to use a dense representation.

If False, the projected data uses a sparse representation if the input is sparse.

random_stateint, RandomState instance or None, default=None

Controls the pseudo random number generator used to generate the projection matrix at fit time. Pass an int for reproducible output across multiple function calls. See Glossary.

Attributes

n_components_int

Concrete number of components computed when n_components=”auto”.

components_sparse matrix of shape (n_components, n_features)

Random matrix used for the projection. Sparse matrix will be of CSR format.

density_float in range 0.0 - 1.0

Concrete density computed from when density = “auto”.

See also

GaussianRandomProjection

References

1

Ping Li, T. Hastie and K. W. Church, 2006, “Very Sparse Random Projections”. https://web.stanford.edu/~hastie/Papers/Ping/KDD06_rp.pdf

2

D. Achlioptas, 2001, “Database-friendly random projections”, https://users.soe.ucsc.edu/~optas/papers/jl.pdf

Examples

>>> import numpy as np
>>> from sklearn.random_projection import SparseRandomProjection
>>> rng = np.random.RandomState(42)
>>> X = rng.rand(100, 10000)
>>> transformer = SparseRandomProjection(random_state=rng)
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(100, 3947)
>>> # very few components are non-zero
>>> np.mean(transformer.components_ != 0)
0.0100...

Methods

fit(X[, y])	Generate a sparse random projection matrix.
fit_transform(X[, y])	Fit to data, then transform it.
get_params([deep])	Get parameters for this estimator.
set_params(**params)	Set the parameters of this estimator.
transform(X)	Project the data by using matrix product with the random matrix

fit(X, y=None)[source]¶

Generate a sparse random projection matrix.

Parameters

X{ndarray, sparse matrix} of shape (n_samples, n_features)

Training set: only the shape is used to find optimal random matrix dimensions based on the theory referenced in the afore mentioned papers.

y

Ignored

Returns

self

fit_transform(X, y=None, **fit_params)[source]¶

Fit to data, then transform it.

Fits transformer to X and y with optional parameters fit_params and returns a transformed version of X.

Parameters

Xarray-like of shape (n_samples, n_features)

Input samples.

yarray-like of shape (n_samples,) or (n_samples, n_outputs), default=None

Target values (None for unsupervised transformations).

**fit_paramsdict

Additional fit parameters.

Returns

X_newndarray array of shape (n_samples, n_features_new)

Transformed array.

get_params(deep=True)[source]¶

Get parameters for this estimator.

Parameters

deepbool, default=True

If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns

paramsdict

Parameter names mapped to their values.

set_params(**params)[source]¶

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as Pipeline). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters

**paramsdict

Estimator parameters.

Returns

selfestimator instance

Estimator instance.

transform(X)[source]¶

Project the data by using matrix product with the random matrix

Parameters

X{ndarray, sparse matrix} of shape (n_samples, n_features)

The input data to project into a smaller dimensional space.

Returns

X_new{ndarray, sparse matrix} of shape (n_samples, n_components)

Projected array.

Examples using sklearn.random_projection.SparseRandomProjection¶