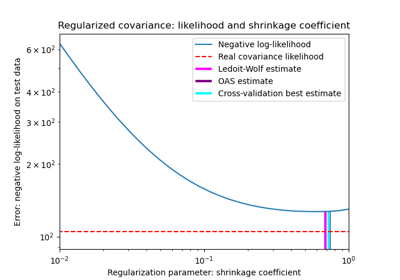
sklearn.covariance.ShrunkCovariance¶

class sklearn.covariance.ShrunkCovariance(*, store_precision=True, assume_centered=False, shrinkage=0.1)[source]¶

Covariance estimator with shrinkage

Read more in the User Guide.

Parameters

store_precisionbool, default=True

Specify if the estimated precision is stored

assume_centeredbool, default=False

If True, data will not be centered before computation. Useful when working with data whose mean is almost, but not exactly zero. If False, data will be centered before computation.

shrinkagefloat, default=0.1

Coefficient in the convex combination used for the computation of the shrunk estimate. Range is [0, 1].

Attributes

covariance_ndarray of shape (n_features, n_features)

Estimated covariance matrix

location_ndarray of shape (n_features,)

Estimated location, i.e. the estimated mean.

precision_ndarray of shape (n_features, n_features)

Estimated pseudo inverse matrix. (stored only if store_precision is True)

Notes

The regularized covariance is given by:

(1 - shrinkage) * cov + shrinkage * mu * np.identity(n_features)

where mu = trace(cov) / n_features

Examples

>>> import numpy as np
>>> from sklearn.covariance import ShrunkCovariance
>>> from sklearn.datasets import make_gaussian_quantiles
>>> real_cov = np.array([[.8, .3],
...                      [.3, .4]])
>>> rng = np.random.RandomState(0)
>>> X = rng.multivariate_normal(mean=[0, 0],
...                                   cov=real_cov,
...                                   size=500)
>>> cov = ShrunkCovariance().fit(X)
>>> cov.covariance_
array([[0.7387..., 0.2536...],
       [0.2536..., 0.4110...]])
>>> cov.location_
array([0.0622..., 0.0193...])

Methods

error_norm(comp_cov[, norm, scaling, squared])	Computes the Mean Squared Error between two covariance estimators.
fit(X[, y])	Fit the shrunk covariance model according to the given training data and parameters.
get_params([deep])	Get parameters for this estimator.
get_precision()	Getter for the precision matrix.
mahalanobis(X)	Computes the squared Mahalanobis distances of given observations.
score(X_test[, y])	Computes the log-likelihood of a Gaussian data set with self.covariance_ as an estimator of its covariance matrix.
set_params(**params)	Set the parameters of this estimator.

error_norm(comp_cov, norm='frobenius', scaling=True, squared=True)[source]¶

Computes the Mean Squared Error between two covariance estimators. (In the sense of the Frobenius norm).

Parameters

comp_covarray-like of shape (n_features, n_features)

The covariance to compare with.

norm{“frobenius”, “spectral”}, default=”frobenius”

The type of norm used to compute the error. Available error types: - ‘frobenius’ (default): sqrt(tr(A^t.A)) - ‘spectral’: sqrt(max(eigenvalues(A^t.A)) where A is the error (comp_cov - self.covariance_).

scalingbool, default=True

If True (default), the squared error norm is divided by n_features. If False, the squared error norm is not rescaled.

squaredbool, default=True

Whether to compute the squared error norm or the error norm. If True (default), the squared error norm is returned. If False, the error norm is returned.

Returns

resultfloat

The Mean Squared Error (in the sense of the Frobenius norm) between self and comp_cov covariance estimators.

fit(X, y=None)[source]¶

Fit the shrunk covariance model according to the given training data and parameters.

Parameters

Xarray-like of shape (n_samples, n_features)

Training data, where n_samples is the number of samples and n_features is the number of features.

yIgnored

Not used, present for API consistency by convention.

Returns

selfobject

get_params(deep=True)[source]¶

Get parameters for this estimator.

Parameters

deepbool, default=True

If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns

paramsdict

Parameter names mapped to their values.

get_precision()[source]¶

Getter for the precision matrix.

Returns

precision_array-like of shape (n_features, n_features)

The precision matrix associated to the current covariance object.

mahalanobis(X)[source]¶

Computes the squared Mahalanobis distances of given observations.

Parameters

Xarray-like of shape (n_samples, n_features)

The observations, the Mahalanobis distances of the which we compute. Observations are assumed to be drawn from the same distribution than the data used in fit.

Returns

distndarray of shape (n_samples,)

Squared Mahalanobis distances of the observations.

score(X_test, y=None)[source]¶

Computes the log-likelihood of a Gaussian data set with self.covariance_ as an estimator of its covariance matrix.

Parameters

X_testarray-like of shape (n_samples, n_features)

Test data of which we compute the likelihood, where n_samples is the number of samples and n_features is the number of features. X_test is assumed to be drawn from the same distribution than the data used in fit (including centering).

yIgnored

Not used, present for API consistency by convention.

Returns

resfloat

The likelihood of the data set with self.covariance_ as an estimator of its covariance matrix.

set_params(**params)[source]¶

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as Pipeline). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters

**paramsdict

Estimator parameters.

Returns

selfestimator instance

Estimator instance.

Examples using sklearn.covariance.ShrunkCovariance¶