Note
Click here to download the full example code or to run this example in your browser via Binder
Polynomial interpolation¶
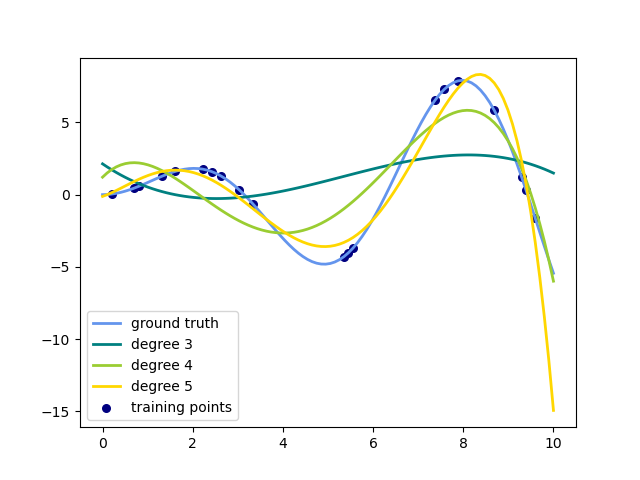
This example demonstrates how to approximate a function with a polynomial of degree n_degree by using ridge regression. Concretely, from n_samples 1d points, it suffices to build the Vandermonde matrix, which is n_samples x n_degree+1 and has the following form:
- [[1, x_1, x_1 ** 2, x_1 ** 3, …],
[1, x_2, x_2 ** 2, x_2 ** 3, …], …]
Intuitively, this matrix can be interpreted as a matrix of pseudo features (the points raised to some power). The matrix is akin to (but different from) the matrix induced by a polynomial kernel.
This example shows that you can do non-linear regression with a linear model, using a pipeline to add non-linear features. Kernel methods extend this idea and can induce very high (even infinite) dimensional feature spaces.
print(__doc__)
# Author: Mathieu Blondel
# Jake Vanderplas
# License: BSD 3 clause
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
def f(x):
""" function to approximate by polynomial interpolation"""
return x * np.sin(x)
# generate points used to plot
x_plot = np.linspace(0, 10, 100)
# generate points and keep a subset of them
x = np.linspace(0, 10, 100)
rng = np.random.RandomState(0)
rng.shuffle(x)
x = np.sort(x[:20])
y = f(x)
# create matrix versions of these arrays
X = x[:, np.newaxis]
X_plot = x_plot[:, np.newaxis]
colors = ['teal', 'yellowgreen', 'gold']
lw = 2
plt.plot(x_plot, f(x_plot), color='cornflowerblue', linewidth=lw,
label="ground truth")
plt.scatter(x, y, color='navy', s=30, marker='o', label="training points")
for count, degree in enumerate([3, 4, 5]):
model = make_pipeline(PolynomialFeatures(degree), Ridge())
model.fit(X, y)
y_plot = model.predict(X_plot)
plt.plot(x_plot, y_plot, color=colors[count], linewidth=lw,
label="degree %d" % degree)
plt.legend(loc='lower left')
plt.show()
Total running time of the script: ( 0 minutes 0.127 seconds)

