Note
Click here to download the full example code or to run this example in your browser via Binder
Gaussian process regression (GPR) with noise-level estimation¶
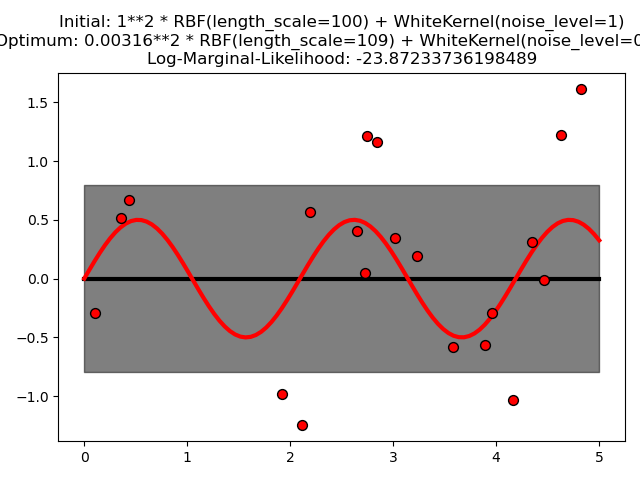
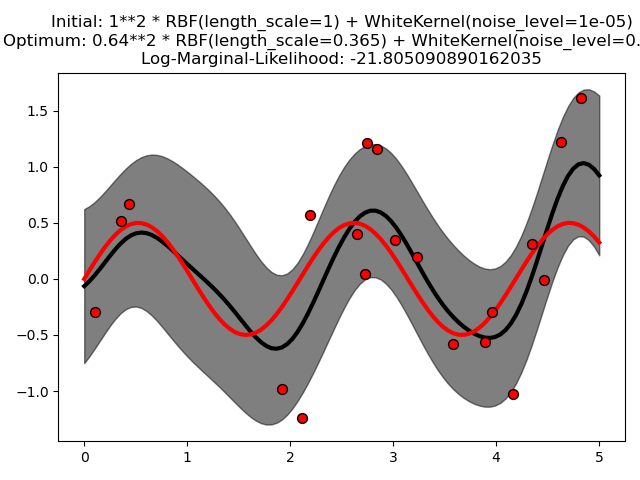
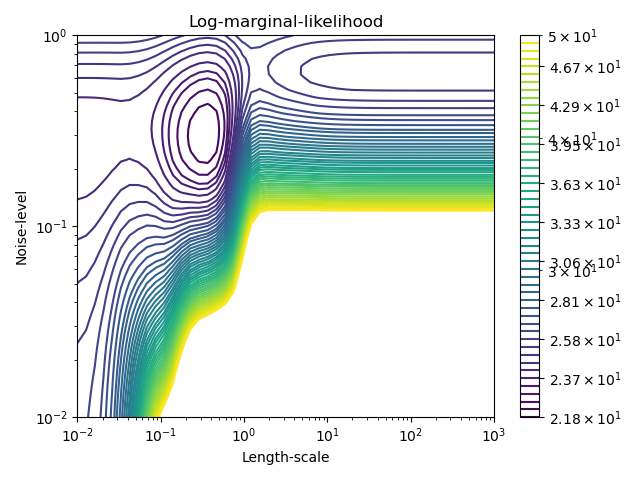
This example illustrates that GPR with a sum-kernel including a WhiteKernel can estimate the noise level of data. An illustration of the log-marginal-likelihood (LML) landscape shows that there exist two local maxima of LML. The first corresponds to a model with a high noise level and a large length scale, which explains all variations in the data by noise. The second one has a smaller noise level and shorter length scale, which explains most of the variation by the noise-free functional relationship. The second model has a higher likelihood; however, depending on the initial value for the hyperparameters, the gradient-based optimization might also converge to the high-noise solution. It is thus important to repeat the optimization several times for different initializations.
Out:
/home/circleci/project/sklearn/gaussian_process/kernels.py:402: ConvergenceWarning: The optimal value found for dimension 0 of parameter k1__k1__constant_value is close to the specified lower bound 1e-05. Decreasing the bound and calling fit again may find a better value.
warnings.warn("The optimal value found for "
print(__doc__)
# Authors: Jan Hendrik Metzen <jhm@informatik.uni-bremen.de>
#
# License: BSD 3 clause
import numpy as np
from matplotlib import pyplot as plt
from matplotlib.colors import LogNorm
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, WhiteKernel
rng = np.random.RandomState(0)
X = rng.uniform(0, 5, 20)[:, np.newaxis]
y = 0.5 * np.sin(3 * X[:, 0]) + rng.normal(0, 0.5, X.shape[0])
# First run
plt.figure()
kernel = 1.0 * RBF(length_scale=100.0, length_scale_bounds=(1e-2, 1e3)) \
+ WhiteKernel(noise_level=1, noise_level_bounds=(1e-10, 1e+1))
gp = GaussianProcessRegressor(kernel=kernel,
alpha=0.0).fit(X, y)
X_ = np.linspace(0, 5, 100)
y_mean, y_cov = gp.predict(X_[:, np.newaxis], return_cov=True)
plt.plot(X_, y_mean, 'k', lw=3, zorder=9)
plt.fill_between(X_, y_mean - np.sqrt(np.diag(y_cov)),
y_mean + np.sqrt(np.diag(y_cov)),
alpha=0.5, color='k')
plt.plot(X_, 0.5*np.sin(3*X_), 'r', lw=3, zorder=9)
plt.scatter(X[:, 0], y, c='r', s=50, zorder=10, edgecolors=(0, 0, 0))
plt.title("Initial: %s\nOptimum: %s\nLog-Marginal-Likelihood: %s"
% (kernel, gp.kernel_,
gp.log_marginal_likelihood(gp.kernel_.theta)))
plt.tight_layout()
# Second run
plt.figure()
kernel = 1.0 * RBF(length_scale=1.0, length_scale_bounds=(1e-2, 1e3)) \
+ WhiteKernel(noise_level=1e-5, noise_level_bounds=(1e-10, 1e+1))
gp = GaussianProcessRegressor(kernel=kernel,
alpha=0.0).fit(X, y)
X_ = np.linspace(0, 5, 100)
y_mean, y_cov = gp.predict(X_[:, np.newaxis], return_cov=True)
plt.plot(X_, y_mean, 'k', lw=3, zorder=9)
plt.fill_between(X_, y_mean - np.sqrt(np.diag(y_cov)),
y_mean + np.sqrt(np.diag(y_cov)),
alpha=0.5, color='k')
plt.plot(X_, 0.5*np.sin(3*X_), 'r', lw=3, zorder=9)
plt.scatter(X[:, 0], y, c='r', s=50, zorder=10, edgecolors=(0, 0, 0))
plt.title("Initial: %s\nOptimum: %s\nLog-Marginal-Likelihood: %s"
% (kernel, gp.kernel_,
gp.log_marginal_likelihood(gp.kernel_.theta)))
plt.tight_layout()
# Plot LML landscape
plt.figure()
theta0 = np.logspace(-2, 3, 49)
theta1 = np.logspace(-2, 0, 50)
Theta0, Theta1 = np.meshgrid(theta0, theta1)
LML = [[gp.log_marginal_likelihood(np.log([0.36, Theta0[i, j], Theta1[i, j]]))
for i in range(Theta0.shape[0])] for j in range(Theta0.shape[1])]
LML = np.array(LML).T
vmin, vmax = (-LML).min(), (-LML).max()
vmax = 50
level = np.around(np.logspace(np.log10(vmin), np.log10(vmax), 50), decimals=1)
plt.contour(Theta0, Theta1, -LML,
levels=level, norm=LogNorm(vmin=vmin, vmax=vmax))
plt.colorbar()
plt.xscale("log")
plt.yscale("log")
plt.xlabel("Length-scale")
plt.ylabel("Noise-level")
plt.title("Log-marginal-likelihood")
plt.tight_layout()
plt.show()
Total running time of the script: ( 0 minutes 3.523 seconds)