1.3. Kernel ridge regression¶

Kernel ridge regression (KRR) [M2012] combines Ridge regression and classification (linear least squares with l2-norm regularization) with the kernel trick. It thus learns a linear function in the space induced by the respective kernel and the data. For non-linear kernels, this corresponds to a non-linear function in the original space.

The form of the model learned by KernelRidge is identical to support vector regression (SVR). However, different loss functions are used: KRR uses squared error loss while support vector regression uses \(\epsilon\)-insensitive loss, both combined with l2 regularization. In contrast to SVR, fitting KernelRidge can be done in closed-form and is typically faster for medium-sized datasets. On the other hand, the learned model is non-sparse and thus slower than SVR, which learns a sparse model for \(\epsilon > 0\), at prediction-time.

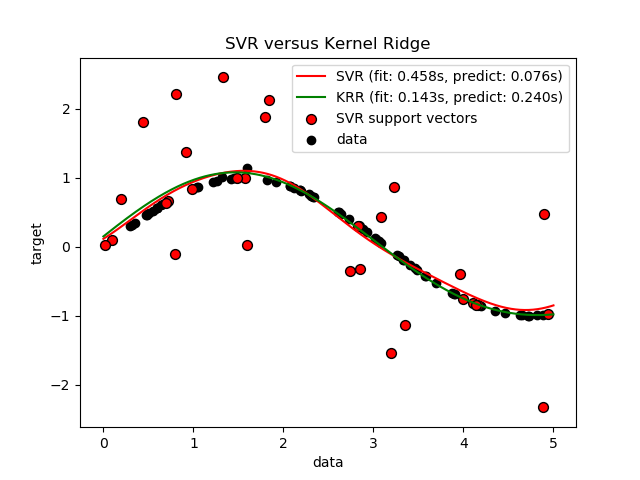
The following figure compares KernelRidge and SVR on an artificial dataset, which consists of a sinusoidal target function and strong noise added to every fifth datapoint. The learned model of KernelRidge and SVR is plotted, where both complexity/regularization and bandwidth of the RBF kernel have been optimized using grid-search. The learned functions are very similar; however, fitting KernelRidge is approx. seven times faster than fitting SVR (both with grid-search). However, prediction of 100000 target values is more than three times faster with SVR since it has learned a sparse model using only approx. 1/3 of the 100 training datapoints as support vectors.

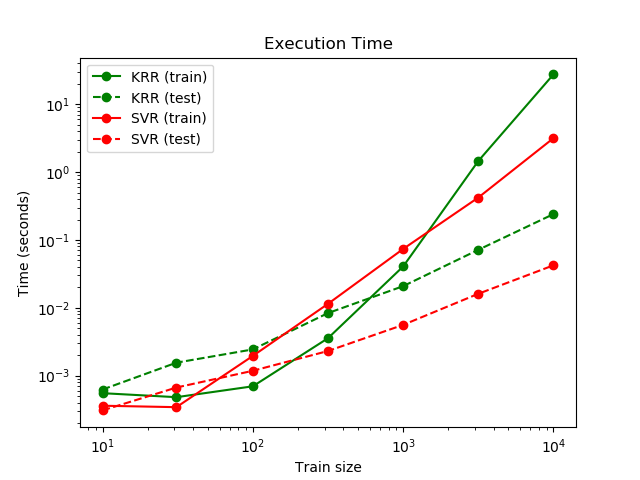
The next figure compares the time for fitting and prediction of KernelRidge and SVR for different sizes of the training set. Fitting KernelRidge is faster than SVR for medium-sized training sets (less than 1000 samples); however, for larger training sets SVR scales better. With regard to prediction time, SVR is faster than KernelRidge for all sizes of the training set because of the learned sparse solution. Note that the degree of sparsity and thus the prediction time depends on the parameters \(\epsilon\) and \(C\) of the SVR; \(\epsilon = 0\) would correspond to a dense model.