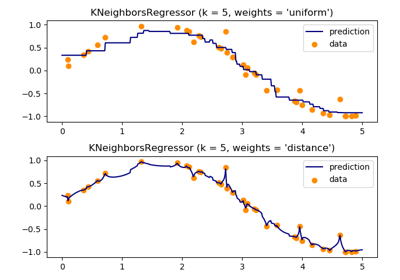
sklearn.neighbors.KNeighborsRegressor¶
-
class
sklearn.neighbors.KNeighborsRegressor(n_neighbors=5, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=None, **kwargs)[source]¶ Regression based on k-nearest neighbors.
The target is predicted by local interpolation of the targets associated of the nearest neighbors in the training set.
Read more in the User Guide.
New in version 0.9.
- Parameters
- n_neighborsint, optional (default = 5)
Number of neighbors to use by default for
kneighborsqueries.- weightsstr or callable
weight function used in prediction. Possible values:
‘uniform’ : uniform weights. All points in each neighborhood are weighted equally.
‘distance’ : weight points by the inverse of their distance. in this case, closer neighbors of a query point will have a greater influence than neighbors which are further away.
[callable] : a user-defined function which accepts an array of distances, and returns an array of the same shape containing the weights.
Uniform weights are used by default.
- algorithm{‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}, optional
Algorithm used to compute the nearest neighbors:
‘ball_tree’ will use
BallTree‘kd_tree’ will use
KDTree‘brute’ will use a brute-force search.
‘auto’ will attempt to decide the most appropriate algorithm based on the values passed to
fitmethod.
Note: fitting on sparse input will override the setting of this parameter, using brute force.
- leaf_sizeint, optional (default = 30)
Leaf size passed to BallTree or KDTree. This can affect the speed of the construction and query, as well as the memory required to store the tree. The optimal value depends on the nature of the problem.
- pinteger, optional (default = 2)
Power parameter for the Minkowski metric. When p = 1, this is equivalent to using manhattan_distance (l1), and euclidean_distance (l2) for p = 2. For arbitrary p, minkowski_distance (l_p) is used.
- metricstring or callable, default ‘minkowski’
the distance metric to use for the tree. The default metric is minkowski, and with p=2 is equivalent to the standard Euclidean metric. See the documentation of the DistanceMetric class for a list of available metrics. If metric is “precomputed”, X is assumed to be a distance matrix and must be square during fit. X may be a Glossary, in which case only “nonzero” elements may be considered neighbors.
- metric_paramsdict, optional (default = None)
Additional keyword arguments for the metric function.
- n_jobsint or None, optional (default=None)
The number of parallel jobs to run for neighbors search.
Nonemeans 1 unless in ajoblib.parallel_backendcontext.-1means using all processors. See Glossary for more details. Doesn’t affectfitmethod.
- Attributes
- effective_metric_string or callable
The distance metric to use. It will be same as the
metricparameter or a synonym of it, e.g. ‘euclidean’ if themetricparameter set to ‘minkowski’ andpparameter set to 2.- effective_metric_params_dict
Additional keyword arguments for the metric function. For most metrics will be same with
metric_paramsparameter, but may also contain thepparameter value if theeffective_metric_attribute is set to ‘minkowski’.
Notes
See Nearest Neighbors in the online documentation for a discussion of the choice of
algorithmandleaf_size.Warning
Regarding the Nearest Neighbors algorithms, if it is found that two neighbors, neighbor
k+1andk, have identical distances but different labels, the results will depend on the ordering of the training data.https://en.wikipedia.org/wiki/K-nearest_neighbor_algorithm
Examples
>>> X = [[0], [1], [2], [3]] >>> y = [0, 0, 1, 1] >>> from sklearn.neighbors import KNeighborsRegressor >>> neigh = KNeighborsRegressor(n_neighbors=2) >>> neigh.fit(X, y) KNeighborsRegressor(...) >>> print(neigh.predict([[1.5]])) [0.5]
Methods
fit(self, X, y)Fit the model using X as training data and y as target values
get_params(self[, deep])Get parameters for this estimator.
kneighbors(self[, X, n_neighbors, …])Finds the K-neighbors of a point.
kneighbors_graph(self[, X, n_neighbors, mode])Computes the (weighted) graph of k-Neighbors for points in X
predict(self, X)Predict the target for the provided data
score(self, X, y[, sample_weight])Return the coefficient of determination R^2 of the prediction.
set_params(self, \*\*params)Set the parameters of this estimator.
-
__init__(self, n_neighbors=5, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=None, **kwargs)[source]¶ Initialize self. See help(type(self)) for accurate signature.
-
fit(self, X, y)[source]¶ Fit the model using X as training data and y as target values
- Parameters
- X{array-like, sparse matrix, BallTree, KDTree}
Training data. If array or matrix, shape [n_samples, n_features], or [n_samples, n_samples] if metric=’precomputed’.
- y{array-like, sparse matrix}
- Target values, array of float values, shape = [n_samples]
or [n_samples, n_outputs]
-
get_params(self, deep=True)[source]¶ Get parameters for this estimator.
- Parameters
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns
- paramsmapping of string to any
Parameter names mapped to their values.
-
kneighbors(self, X=None, n_neighbors=None, return_distance=True)[source]¶ Finds the K-neighbors of a point. Returns indices of and distances to the neighbors of each point.
- Parameters
- Xarray-like, shape (n_queries, n_features), or (n_queries, n_indexed) if metric == ‘precomputed’
The query point or points. If not provided, neighbors of each indexed point are returned. In this case, the query point is not considered its own neighbor.
- n_neighborsint
Number of neighbors to get (default is the value passed to the constructor).
- return_distanceboolean, optional. Defaults to True.
If False, distances will not be returned
- Returns
- neigh_distarray, shape (n_queries, n_neighbors)
Array representing the lengths to points, only present if return_distance=True
- neigh_indarray, shape (n_queries, n_neighbors)
Indices of the nearest points in the population matrix.
Examples
In the following example, we construct a NearestNeighbors class from an array representing our data set and ask who’s the closest point to [1,1,1]
>>> samples = [[0., 0., 0.], [0., .5, 0.], [1., 1., .5]] >>> from sklearn.neighbors import NearestNeighbors >>> neigh = NearestNeighbors(n_neighbors=1) >>> neigh.fit(samples) NearestNeighbors(n_neighbors=1) >>> print(neigh.kneighbors([[1., 1., 1.]])) (array([[0.5]]), array([[2]]))
As you can see, it returns [[0.5]], and [[2]], which means that the element is at distance 0.5 and is the third element of samples (indexes start at 0). You can also query for multiple points:
>>> X = [[0., 1., 0.], [1., 0., 1.]] >>> neigh.kneighbors(X, return_distance=False) array([[1], [2]]...)
-
kneighbors_graph(self, X=None, n_neighbors=None, mode='connectivity')[source]¶ Computes the (weighted) graph of k-Neighbors for points in X
- Parameters
- Xarray-like, shape (n_queries, n_features), or (n_queries, n_indexed) if metric == ‘precomputed’
The query point or points. If not provided, neighbors of each indexed point are returned. In this case, the query point is not considered its own neighbor.
- n_neighborsint
Number of neighbors for each sample. (default is value passed to the constructor).
- mode{‘connectivity’, ‘distance’}, optional
Type of returned matrix: ‘connectivity’ will return the connectivity matrix with ones and zeros, in ‘distance’ the edges are Euclidean distance between points.
- Returns
- Asparse graph in CSR format, shape = [n_queries, n_samples_fit]
n_samples_fit is the number of samples in the fitted data A[i, j] is assigned the weight of edge that connects i to j.
Examples
>>> X = [[0], [3], [1]] >>> from sklearn.neighbors import NearestNeighbors >>> neigh = NearestNeighbors(n_neighbors=2) >>> neigh.fit(X) NearestNeighbors(n_neighbors=2) >>> A = neigh.kneighbors_graph(X) >>> A.toarray() array([[1., 0., 1.], [0., 1., 1.], [1., 0., 1.]])
-
predict(self, X)[source]¶ Predict the target for the provided data
- Parameters
- Xarray-like, shape (n_queries, n_features), or (n_queries, n_indexed) if metric == ‘precomputed’
Test samples.
- Returns
- yarray of int, shape = [n_queries] or [n_queries, n_outputs]
Target values
-
score(self, X, y, sample_weight=None)[source]¶ Return the coefficient of determination R^2 of the prediction.
The coefficient R^2 is defined as (1 - u/v), where u is the residual sum of squares ((y_true - y_pred) ** 2).sum() and v is the total sum of squares ((y_true - y_true.mean()) ** 2).sum(). The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of y, disregarding the input features, would get a R^2 score of 0.0.
- Parameters
- Xarray-like of shape (n_samples, n_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead, shape = (n_samples, n_samples_fitted), where n_samples_fitted is the number of samples used in the fitting for the estimator.
- yarray-like of shape (n_samples,) or (n_samples, n_outputs)
True values for X.
- sample_weightarray-like of shape (n_samples,), default=None
Sample weights.
- Returns
- scorefloat
R^2 of self.predict(X) wrt. y.
Notes
The R2 score used when calling
scoreon a regressor will usemultioutput='uniform_average'from version 0.23 to keep consistent withr2_score. This will influence thescoremethod of all the multioutput regressors (except forMultiOutputRegressor). To specify the default value manually and avoid the warning, please either callr2_scoredirectly or make a custom scorer withmake_scorer(the built-in scorer'r2'usesmultioutput='uniform_average').
-
set_params(self, **params)[source]¶ Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as pipelines). The latter have parameters of the form
<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters
- **paramsdict
Estimator parameters.
- Returns
- selfobject
Estimator instance.