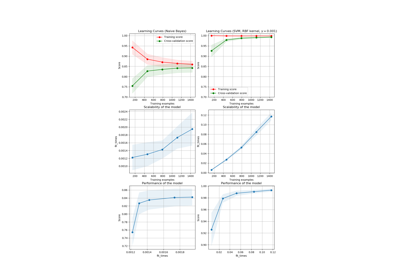
sklearn.model_selection.learning_curve

sklearn.model_selection.learning_curve(estimator, X, y, groups=None, train_sizes=array([0.1, 0.33, 0.55, 0.78, 1. ]), cv=None, scoring=None, exploit_incremental_learning=False, n_jobs=None, pre_dispatch='all', verbose=0, shuffle=False, random_state=None, error_score=nan, return_times=False)[source]

Learning curve.

Determines cross-validated training and test scores for different training set sizes.

A cross-validation generator splits the whole dataset k times in training and test data. Subsets of the training set with varying sizes will be used to train the estimator and a score for each training subset size and the test set will be computed. Afterwards, the scores will be averaged over all k runs for each training subset size.

Read more in the User Guide.

Parameters
estimatorobject type that implements the “fit” and “predict” methods

An object of that type which is cloned for each validation.

Xarray-like, shape (n_samples, n_features)

Training vector, where n_samples is the number of samples and n_features is the number of features.

yarray-like, shape (n_samples) or (n_samples, n_features), optional

Target relative to X for classification or regression; None for unsupervised learning.

groupsarray-like, with shape (n_samples,), optional

Group labels for the samples used while splitting the dataset into train/test set. Only used in conjunction with a “Group” cv instance (e.g., GroupKFold).

train_sizesarray-like, shape (n_ticks,), dtype float or int

Relative or absolute numbers of training examples that will be used to generate the learning curve. If the dtype is float, it is regarded as a fraction of the maximum size of the training set (that is determined by the selected validation method), i.e. it has to be within (0, 1]. Otherwise it is interpreted as absolute sizes of the training sets. Note that for classification the number of samples usually have to be big enough to contain at least one sample from each class. (default: np.linspace(0.1, 1.0, 5))

cvint, cross-validation generator or an iterable, optional

Determines the cross-validation splitting strategy. Possible inputs for cv are:

  • None, to use the default 5-fold cross validation,

  • integer, to specify the number of folds in a (Stratified)KFold,

  • CV splitter,

  • An iterable yielding (train, test) splits as arrays of indices.

For integer/None inputs, if the estimator is a classifier and y is either binary or multiclass, StratifiedKFold is used. In all other cases, KFold is used.

Refer User Guide for the various cross-validation strategies that can be used here.

Changed in version 0.22: cv default value if None changed from 3-fold to 5-fold.

scoringstring, callable or None, optional, default: None

A string (see model evaluation documentation) or a scorer callable object / function with signature scorer(estimator, X, y).

exploit_incremental_learningboolean, optional, default: False

If the estimator supports incremental learning, this will be used to speed up fitting for different training set sizes.

n_jobsint or None, optional (default=None)

Number of jobs to run in parallel. None means 1 unless in a joblib.parallel_backend context. -1 means using all processors. See Glossary for more details.

pre_dispatchinteger or string, optional

Number of predispatched jobs for parallel execution (default is all). The option can reduce the allocated memory. The string can be an expression like ‘2*n_jobs’.

verboseinteger, optional

Controls the verbosity: the higher, the more messages.

shuffleboolean, optional

Whether to shuffle training data before taking prefixes of it based on``train_sizes``.

random_stateint, RandomState instance or None, optional (default=None)

If int, random_state is the seed used by the random number generator; If RandomState instance, random_state is the random number generator; If None, the random number generator is the RandomState instance used by np.random. Used when shuffle is True.

error_score‘raise’ or numeric

Value to assign to the score if an error occurs in estimator fitting. If set to ‘raise’, the error is raised. If a numeric value is given, FitFailedWarning is raised. This parameter does not affect the refit step, which will always raise the error.

return_timesboolean, optional (default: False)

Whether to return the fit and score times.

Returns
train_sizes_absarray, shape (n_unique_ticks,), dtype int

Numbers of training examples that has been used to generate the learning curve. Note that the number of ticks might be less than n_ticks because duplicate entries will be removed.

train_scoresarray, shape (n_ticks, n_cv_folds)

Scores on training sets.

test_scoresarray, shape (n_ticks, n_cv_folds)

Scores on test set.

fit_timesarray, shape (n_ticks, n_cv_folds)

Times spent for fitting in seconds. Only present if return_times is True.

score_timesarray, shape (n_ticks, n_cv_folds)

Times spent for scoring in seconds. Only present if return_times is True.

Notes

See examples/model_selection/plot_learning_curve.py

Examples using sklearn.model_selection.learning_curve