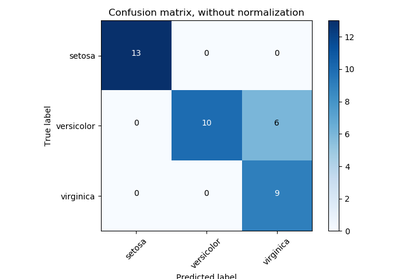
sklearn.metrics.confusion_matrix

sklearn.metrics.confusion_matrix(y_true, y_pred, labels=None, sample_weight=None)[source]

Compute confusion matrix to evaluate the accuracy of a classification

By definition a confusion matrix 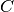C is such that 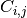C_{i, j} is equal to the number of observations known to be in group 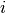i but predicted to be in group j.

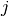Thus in binary classification, the count of true negatives is 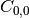C_{0,0}, false negatives is 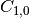C_{1,0}, true positives is C_{1,1} and false positives is C_{0,1}.

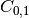Read more in the User Guide.

Parameters:

y_true : array, shape = [n_samples]

Ground truth (correct) target values.

y_pred : array, shape = [n_samples]

Estimated targets as returned by a classifier.

labels : array, shape = [n_classes], optional

List of labels to index the matrix. This may be used to reorder or select a subset of labels. If none is given, those that appear at least once in y_true or y_pred are used in sorted order.

sample_weight : array-like of shape = [n_samples], optional

Sample weights.
Returns:

C : array, shape = [n_classes, n_classes]

Confusion matrix

References

[R206]Wikipedia entry for the Confusion matrix

Examples

>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
       [0, 0, 1],
       [1, 0, 2]])

>>> y_true = ["cat", "ant", "cat", "cat", "ant", "bird"]
>>> y_pred = ["ant", "ant", "cat", "cat", "ant", "cat"]
>>> confusion_matrix(y_true, y_pred, labels=["ant", "bird", "cat"])
array([[2, 0, 0],
       [0, 0, 1],
       [1, 0, 2]])

In the binary case, we can extract true positives, etc as follows:

>>> tn, fp, fn, tp = confusion_matrix([0, 1, 0, 1], [1, 1, 1, 0]).ravel()
>>> (tn, fp, fn, tp)
(0, 2, 1, 1)