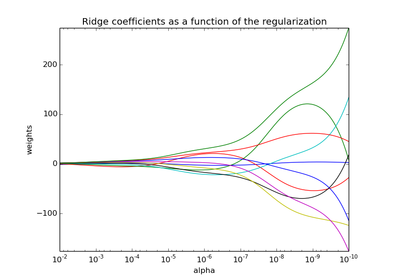
`sklearn.linear_model`.Ridge¶

class sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True, normalize=False, copy_X=True, max_iter=None, tol=0.001, solver='auto')[source]¶

Linear least squares with l2 regularization.

This model solves a regression model where the loss function is the linear least squares function and regularization is given by the l2-norm. Also known as Ridge Regression or Tikhonov regularization. This estimator has built-in support for multi-variate regression (i.e., when y is a 2d-array of shape [n_samples, n_targets]).

Parameters:

alpha : {float, array-like}

shape = [n_targets] Small positive values of alpha improve the conditioning of the problem and reduce the variance of the estimates. Alpha corresponds to (2*C)^-1 in other linear models such as LogisticRegression or LinearSVC. If an array is passed, penalties are assumed to be specific to the targets. Hence they must correspond in number.

copy_X : boolean, optional, default True

If True, X will be copied; else, it may be overwritten.

fit_intercept : boolean

Whether to calculate the intercept for this model. If set to false, no intercept will be used in calculations (e.g. data is expected to be already centered).

max_iter : int, optional

Maximum number of iterations for conjugate gradient solver. The default value is determined by scipy.sparse.linalg.

normalize : boolean, optional, default False

If True, the regressors X will be normalized before regression.

solver : {‘auto’, ‘svd’, ‘cholesky’, ‘lsqr’, ‘sparse_cg’}

Solver to use in the computational routines:

‘auto’ chooses the solver automatically based on the type of data.

‘svd’ uses a Singular Value Decomposition of X to compute the Ridge coefficients. More stable for singular matrices than ‘cholesky’.

‘cholesky’ uses the standard scipy.linalg.solve function to obtain a closed-form solution.

‘sparse_cg’ uses the conjugate gradient solver as found in scipy.sparse.linalg.cg. As an iterative algorithm, this solver is more appropriate than ‘cholesky’ for large-scale data (possibility to set tol and max_iter).

‘lsqr’ uses the dedicated regularized least-squares routine scipy.sparse.linalg.lsqr. It is the fatest but may not be available in old scipy versions. It also uses an iterative procedure.

All three solvers support both dense and sparse data.

tol : float

Precision of the solution.

Attributes:

coef_ : array, shape = [n_features] or [n_targets, n_features]

Weight vector(s).

See also

RidgeClassifier, RidgeCV, KernelRidge

Examples

>>> from sklearn.linear_model import Ridge
>>> import numpy as np
>>> n_samples, n_features = 10, 5
>>> np.random.seed(0)
>>> y = np.random.randn(n_samples)
>>> X = np.random.randn(n_samples, n_features)
>>> clf = Ridge(alpha=1.0)
>>> clf.fit(X, y) 
Ridge(alpha=1.0, copy_X=True, fit_intercept=True, max_iter=None,
      normalize=False, solver='auto', tol=0.001)

Methods

`decision_function`(X)	Decision function of the linear model.
`fit`(X, y[, sample_weight])	Fit Ridge regression model
`get_params`([deep])	Get parameters for this estimator.
`predict`(X)	Predict using the linear model
`score`(X, y[, sample_weight])	Returns the coefficient of determination R^2 of the prediction.
`set_params`(**params)	Set the parameters of this estimator.

__init__(alpha=1.0, fit_intercept=True, normalize=False, copy_X=True, max_iter=None, tol=0.001, solver='auto')[source]¶

decision_function(X)[source]¶

Decision function of the linear model.

Parameters:

X : {array-like, sparse matrix}, shape = (n_samples, n_features)

Samples.

Returns:

C : array, shape = (n_samples,)

Returns predicted values.

fit(X, y, sample_weight=None)[source]¶

Fit Ridge regression model

Parameters:

X : {array-like, sparse matrix}, shape = [n_samples, n_features]

Training data

y : array-like, shape = [n_samples] or [n_samples, n_targets]

Target values

sample_weight : float or numpy array of shape [n_samples]

Individual weights for each sample

Returns:

self : returns an instance of self.

get_params(deep=True)[source]¶

Get parameters for this estimator.

Parameters:

deep: boolean, optional :

If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

params : mapping of string to any

Parameter names mapped to their values.

predict(X)[source]¶

Predict using the linear model

Parameters:

X : {array-like, sparse matrix}, shape = (n_samples, n_features)

Samples.

Returns:

C : array, shape = (n_samples,)

Returns predicted values.

score(X, y, sample_weight=None)[source]¶

Returns the coefficient of determination R^2 of the prediction.

The coefficient R^2 is defined as (1 - u/v), where u is the regression sum of squares ((y_true - y_pred) ** 2).sum() and v is the residual sum of squares ((y_true - y_true.mean()) ** 2).sum(). Best possible score is 1.0, lower values are worse.

Parameters:

X : array-like, shape = (n_samples, n_features)

Test samples.

y : array-like, shape = (n_samples) or (n_samples, n_outputs)

True values for X.

sample_weight : array-like, shape = [n_samples], optional

Sample weights.

Returns:

score : float

R^2 of self.predict(X) wrt. y.

set_params(**params)[source]¶

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as pipelines). The former have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.