`sklearn.linear_model`.LinearRegression¶

class sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True)¶

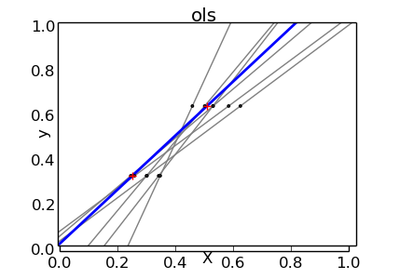
Ordinary least squares Linear Regression.

Parameters:

fit_intercept : boolean, optional

whether to calculate the intercept for this model. If set to false, no intercept will be used in calculations (e.g. data is expected to be already centered).

normalize : boolean, optional, default False

If True, the regressors X will be normalized before regression.

Attributes:

`coef_` : array, shape (n_features, ) or (n_targets, n_features)

Estimated coefficients for the linear regression problem. If multiple targets are passed during the fit (y 2D), this is a 2D array of shape (n_targets, n_features), while if only one target is passed, this is a 1D array of length n_features.

`intercept_` : array

Independent term in the linear model.

Notes

From the implementation point of view, this is just plain Ordinary Least Squares (scipy.linalg.lstsq) wrapped as a predictor object.

Methods

`decision_function`(X)	Decision function of the linear model.
`fit`(X, y[, n_jobs])	Fit linear model.
`get_params`([deep])	Get parameters for this estimator.
`predict`(X)	Predict using the linear model
`score`(X, y[, sample_weight])	Returns the coefficient of determination R^2 of the prediction.
`set_params`(**params)	Set the parameters of this estimator.

__init__(fit_intercept=True, normalize=False, copy_X=True)¶

decision_function(X)¶

Decision function of the linear model.

Parameters:

X : {array-like, sparse matrix}, shape = (n_samples, n_features)

Samples.

Returns:

C : array, shape = (n_samples,)

Returns predicted values.

fit(X, y, n_jobs=1)¶

Fit linear model.

Parameters:

X : numpy array or sparse matrix of shape [n_samples,n_features]

Training data

y : numpy array of shape [n_samples, n_targets]

Target values

n_jobs : The number of jobs to use for the computation.

If -1 all CPUs are used. This will only provide speedup for n_targets > 1 and sufficient large problems

Returns:

self : returns an instance of self.

get_params(deep=True)¶

Get parameters for this estimator.

Parameters:

deep: boolean, optional :

If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

params : mapping of string to any

Parameter names mapped to their values.

predict(X)¶

Predict using the linear model

Parameters:

X : {array-like, sparse matrix}, shape = (n_samples, n_features)

Samples.

Returns:

C : array, shape = (n_samples,)

Returns predicted values.

score(X, y, sample_weight=None)¶

Returns the coefficient of determination R^2 of the prediction.

The coefficient R^2 is defined as (1 - u/v), where u is the regression sum of squares ((y_true - y_pred) ** 2).sum() and v is the residual sum of squares ((y_true - y_true.mean()) ** 2).sum(). Best possible score is 1.0, lower values are worse.

Parameters:

X : array-like, shape = (n_samples, n_features)

Test samples.

y : array-like, shape = (n_samples,)

True values for X.

sample_weight : array-like, shape = [n_samples], optional

Sample weights.

Returns:

score : float

R^2 of self.predict(X) wrt. y.

set_params(**params)¶

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as pipelines). The former have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.