Partial Dependence Plots¶
Partial dependence plots show the dependence between the target function [1] and a set of ‘target’ features, marginalizing over the values of all other features (the complement features). Due to the limits of human perception the size of the target feature set must be small (usually, one or two) thus the target features are usually chosen among the most important features (see feature_importances_).
This example shows how to obtain partial dependence plots from a GradientBoostingRegressor trained on the California housing dataset. The example is taken from [HTF2009].
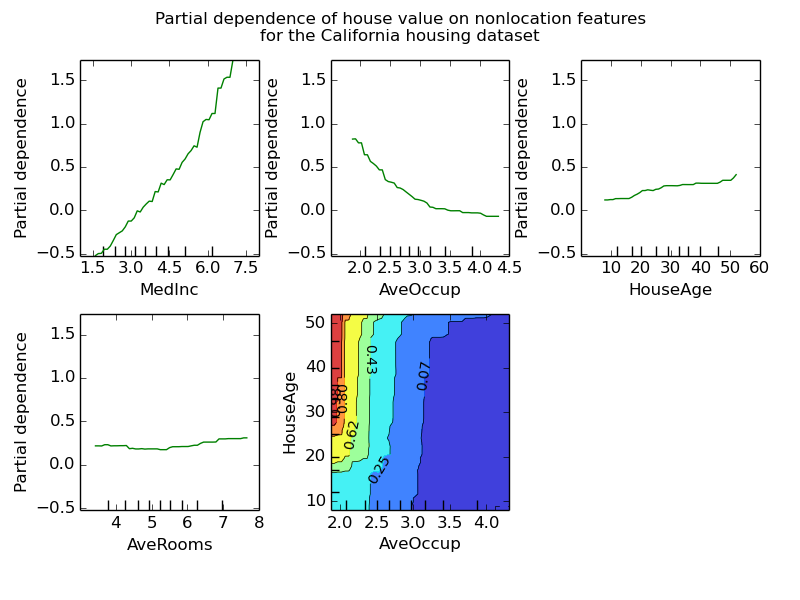
The plot shows four one-way and one two-way partial dependence plots. The target variables for the one-way PDP are: median income (MedInc), avg. occupants per household (AvgOccup), median house age (HouseAge), and avg. rooms per household (AveRooms).
We can clearly see that the median house price shows a linear relationship with the median income (top left) and that the house price drops when the avg. occupants per household increases (top middle). The top right plot shows that the house age in a district does not have a strong influence on the (median) house price; so does the average rooms per household. The tick marks on the x-axis represent the deciles of the feature values in the training data.
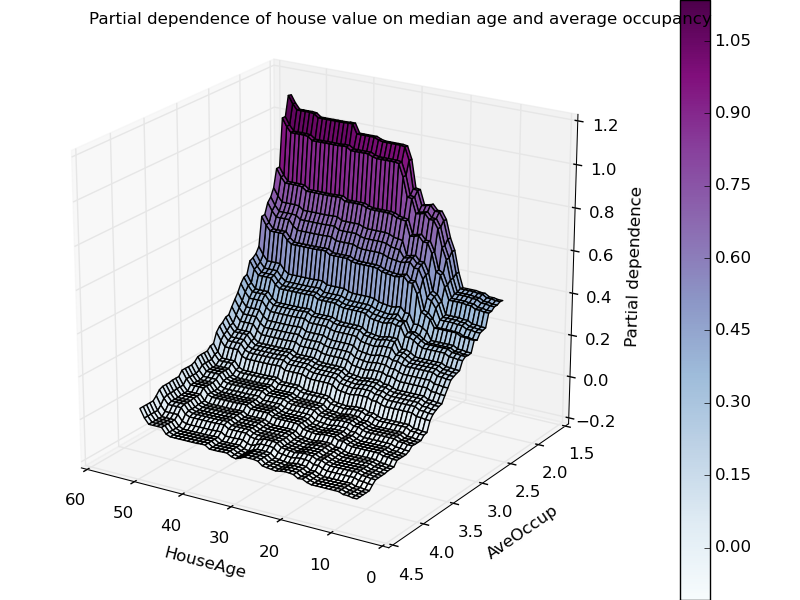
Partial dependence plots with two target features enable us to visualize interactions among them. The two-way partial dependence plot shows the dependence of median house price on joint values of house age and avg. occupants per household. We can clearly see an interaction between the two features: For an avg. occupancy greater than two, the house price is nearly independent of the house age, whereas for values less than two there is a strong dependence on age.
| [HTF2009] | T. Hastie, R. Tibshirani and J. Friedman, “Elements of Statistical Learning Ed. 2”, Springer, 2009. |
| [1] | For classification you can think of it as the regression score before the link function. |
Script output:
________________________________________________________________________________
Training GBRT...
done.
________________________________________________________________________________
Convenience plot with ``partial_dependence_plots``
________________________________________________________________________________
Custom 3d plot via ``partial_dependence``
Python source code: plot_partial_dependence.py
print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.cross_validation import train_test_split
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.ensemble.partial_dependence import plot_partial_dependence
from sklearn.ensemble.partial_dependence import partial_dependence
from sklearn.datasets.california_housing import fetch_california_housing
# fetch California housing dataset
cal_housing = fetch_california_housing()
# split 80/20 train-test
X_train, X_test, y_train, y_test = train_test_split(cal_housing.data,
cal_housing.target,
test_size=0.2,
random_state=1)
names = cal_housing.feature_names
print('_' * 80)
print("Training GBRT...")
clf = GradientBoostingRegressor(n_estimators=100, max_depth=4,
learning_rate=0.1, loss='huber',
random_state=1)
clf.fit(X_train, y_train)
print("done.")
print('_' * 80)
print('Convenience plot with ``partial_dependence_plots``')
print
features = [0, 5, 1, 2, (5, 1)]
fig, axs = plot_partial_dependence(clf, X_train, features, feature_names=names,
n_jobs=3, grid_resolution=50)
fig.suptitle('Partial dependence of house value on nonlocation features\n'
'for the California housing dataset')
plt.subplots_adjust(top=0.9) # tight_layout causes overlap with suptitle
print('_' * 80)
print('Custom 3d plot via ``partial_dependence``')
print
fig = plt.figure()
target_feature = (1, 5)
pdp, (x_axis, y_axis) = partial_dependence(clf, target_feature,
X=X_train, grid_resolution=50)
XX, YY = np.meshgrid(x_axis, y_axis)
Z = pdp.T.reshape(XX.shape).T
ax = Axes3D(fig)
surf = ax.plot_surface(XX, YY, Z, rstride=1, cstride=1, cmap=plt.cm.BuPu)
ax.set_xlabel(names[target_feature[0]])
ax.set_ylabel(names[target_feature[1]])
ax.set_zlabel('Partial dependence')
# pretty init view
ax.view_init(elev=22, azim=122)
plt.colorbar(surf)
plt.suptitle('Partial dependence of house value on median age and '
'average occupancy')
plt.subplots_adjust(top=0.9)
plt.show()
Total running time of the example: 4.65 seconds ( 0 minutes 4.65 seconds)