3.3. Tuning the decision threshold for class prediction#
Classification is best divided into two parts:
the statistical problem of learning a model to predict, ideally, class probabilities;
the decision problem to take concrete action based on those probability predictions.
Let’s take a straightforward example related to weather forecasting: the first point is related to answering “what is the chance that it will rain tomorrow?” while the second point is related to answering “should I take an umbrella tomorrow?”.
When it comes to the scikit-learn API, the first point is addressed providing scores using predict_proba or decision_function. The former returns conditional probability estimates \(P(y|X)\) for each class, while the latter returns a decision score for each class.
The decision corresponding to the labels are obtained with predict. In binary classification, a decision rule or action is then defined by thresholding the scores, leading to the prediction of a single class label for each sample. For binary classification in scikit-learn, class labels predictions are obtained by hard-coded cut-off rules: a positive class is predicted when the conditional probability \(P(y|X)\) is greater than 0.5 (obtained with predict_proba) or if the decision score is greater than 0 (obtained with decision_function).
Here, we show an example that illustrates the relation between conditional probability estimates \(P(y|X)\) and class labels:
>>> from sklearn.datasets import make_classification
>>> from sklearn.tree import DecisionTreeClassifier
>>> X, y = make_classification(random_state=0)
>>> classifier = DecisionTreeClassifier(max_depth=2, random_state=0).fit(X, y)
>>> classifier.predict_proba(X[:4])
array([[0.94 , 0.06 ],
[0.94 , 0.06 ],
[0.0416..., 0.9583...],
[0.0416..., 0.9583...]])
>>> classifier.predict(X[:4])
array([0, 0, 1, 1])
While these hard-coded rules might at first seem reasonable as default behavior, they are most certainly not ideal for most use cases. Let’s illustrate with an example.
Consider a scenario where a predictive model is being deployed to assist physicians in detecting tumors. In this setting, physicians will most likely be interested in identifying all patients with cancer and not missing anyone with cancer so that they can provide them with the right treatment. In other words, physicians prioritize achieving a high recall rate. This emphasis on recall comes, of course, with the trade-off of potentially more false-positive predictions, reducing the precision of the model. That is a risk physicians are willing to take because the cost of a missed cancer is much higher than the cost of further diagnostic tests. Consequently, when it comes to deciding whether to classify a patient as having cancer or not, it may be more beneficial to classify them as positive for cancer when the conditional probability estimate is much lower than 0.5.
3.3.1. Post-tuning the decision threshold#
One solution to address the problem stated in the introduction is to tune the decision
threshold of the classifier once the model has been trained. The
TunedThresholdClassifierCV tunes this threshold using
an internal cross-validation. The optimum threshold is chosen to maximize a given
metric.
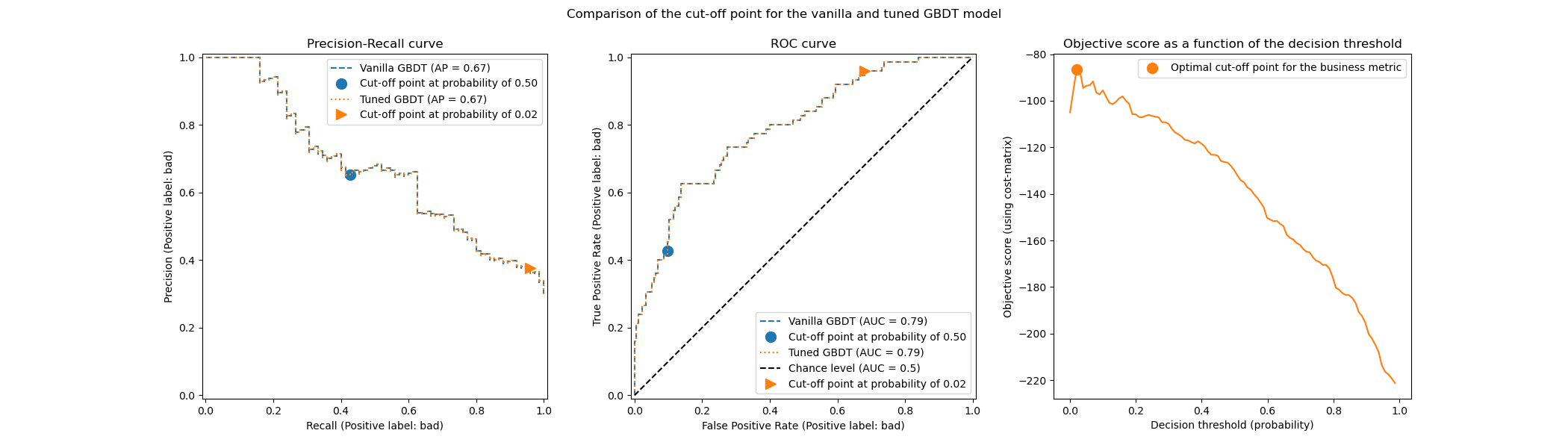
The following image illustrates the tuning of the decision threshold for a gradient boosting classifier. While the vanilla and tuned classifiers provide the same predict_proba outputs and thus the same Receiver Operating Characteristic (ROC) and Precision-Recall curves, the class label predictions differ because of the tuned decision threshold. The vanilla classifier predicts the class of interest for a conditional probability greater than 0.5 while the tuned classifier predicts the class of interest for a very low probability (around 0.02). This decision threshold optimizes a utility metric defined by the business (in this case an insurance company).
3.3.1.1. Options to tune the decision threshold#
The decision threshold can be tuned through different strategies controlled by the
parameter scoring.
One way to tune the threshold is by maximizing a pre-defined scikit-learn metric. These
metrics can be found by calling the function get_scorer_names.
By default, the balanced accuracy is the metric used but be aware that one should choose
a meaningful metric for their use case.
Note
It is important to notice that these metrics come with default parameters, notably
the label of the class of interest (i.e. pos_label). Thus, if this label is not
the right one for your application, you need to define a scorer and pass the right
pos_label (and additional parameters) using the
make_scorer. Refer to Defining your scoring strategy from metric functions to get
information to define your own scoring function. For instance, we show how to pass
the information to the scorer that the label of interest is 0 when maximizing the
f1_score:
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.model_selection import TunedThresholdClassifierCV
>>> from sklearn.metrics import make_scorer, f1_score
>>> X, y = make_classification(
... n_samples=1_000, weights=[0.1, 0.9], random_state=0)
>>> pos_label = 0
>>> scorer = make_scorer(f1_score, pos_label=pos_label)
>>> base_model = LogisticRegression()
>>> model = TunedThresholdClassifierCV(base_model, scoring=scorer)
>>> scorer(model.fit(X, y), X, y)
0.88...
>>> # compare it with the internal score found by cross-validation
>>> model.best_score_
0.86...
3.3.1.2. Important notes regarding the internal cross-validation#
By default TunedThresholdClassifierCV uses a 5-fold
stratified cross-validation to tune the decision threshold. The parameter cv allows to
control the cross-validation strategy. It is possible to bypass cross-validation by
setting cv="prefit" and providing a fitted classifier. In this case, the decision
threshold is tuned on the data provided to the fit method.
However, you should be extremely careful when using this option. You should never use
the same data for training the classifier and tuning the decision threshold due to the
risk of overfitting. Refer to the following example section for more details (cf.
Consideration regarding model refitting and cross-validation). If you have limited resources, consider using
a float number for cv to limit to an internal single train-test split.
The option cv="prefit" should only be used when the provided classifier was already
trained, and you just want to find the best decision threshold using a new validation
set.
3.3.1.3. Manually setting the decision threshold#
The previous sections discussed strategies to find an optimal decision threshold. It is
also possible to manually set the decision threshold using the class
FixedThresholdClassifier.
3.3.1.4. Examples#
See the example entitled Post-hoc tuning the cut-off point of decision function, to get insights on the post-tuning of the decision threshold.
See the example entitled Post-tuning the decision threshold for cost-sensitive learning, to learn about cost-sensitive learning and decision threshold tuning.
