Note
Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder
SVM-Anova: SVM with univariate feature selection¶
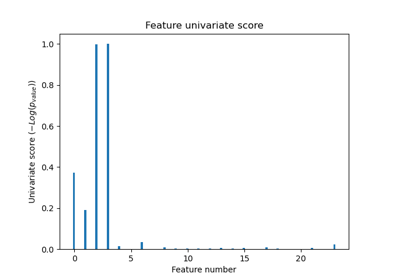
This example shows how to perform univariate feature selection before running a SVC (support vector classifier) to improve the classification scores. We use the iris dataset (4 features) and add 36 non-informative features. We can find that our model achieves best performance when we select around 10% of features.
Load some data to play with¶
import numpy as np
from sklearn.datasets import load_iris
X, y = load_iris(return_X_y=True)
# Add non-informative features
rng = np.random.RandomState(0)
X = np.hstack((X, 2 * rng.random((X.shape[0], 36))))
Create the pipeline¶
from sklearn.feature_selection import SelectPercentile, f_classif
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
# Create a feature-selection transform, a scaler and an instance of SVM that we
# combine together to have a full-blown estimator
clf = Pipeline(
[
("anova", SelectPercentile(f_classif)),
("scaler", StandardScaler()),
("svc", SVC(gamma="auto")),
]
)
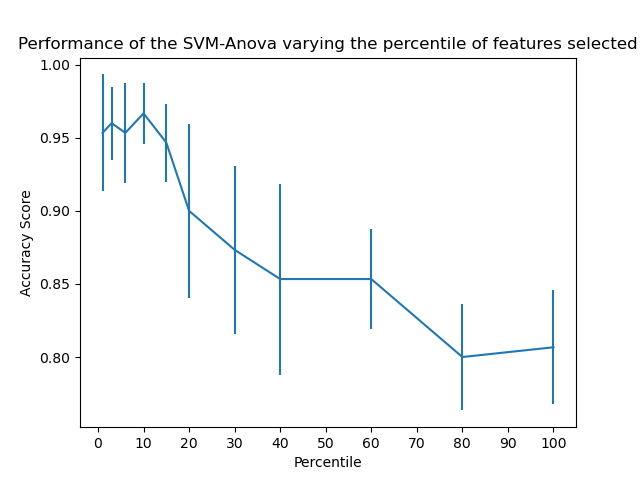
Plot the cross-validation score as a function of percentile of features¶
import matplotlib.pyplot as plt
from sklearn.model_selection import cross_val_score
score_means = list()
score_stds = list()
percentiles = (1, 3, 6, 10, 15, 20, 30, 40, 60, 80, 100)
for percentile in percentiles:
clf.set_params(anova__percentile=percentile)
this_scores = cross_val_score(clf, X, y)
score_means.append(this_scores.mean())
score_stds.append(this_scores.std())
plt.errorbar(percentiles, score_means, np.array(score_stds))
plt.title("Performance of the SVM-Anova varying the percentile of features selected")
plt.xticks(np.linspace(0, 100, 11, endpoint=True))
plt.xlabel("Percentile")
plt.ylabel("Accuracy Score")
plt.axis("tight")
plt.show()
Total running time of the script: (0 minutes 0.309 seconds)
Related examples
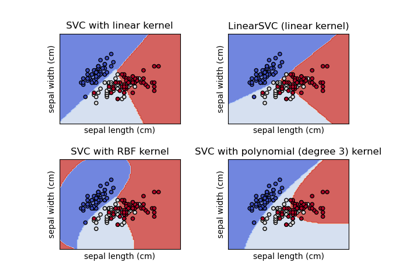
Plot different SVM classifiers in the iris dataset
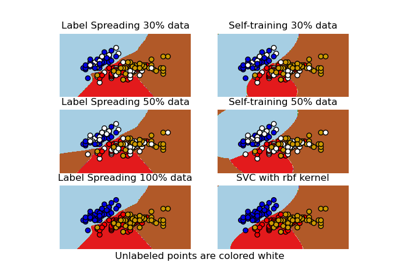
Decision boundary of semi-supervised classifiers versus SVM on the Iris dataset