Nearest Neighbors regression¶

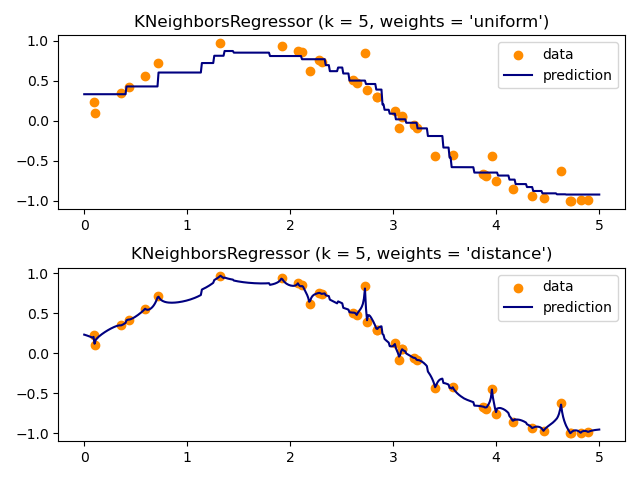
Demonstrate the resolution of a regression problem using a k-Nearest Neighbor and the interpolation of the target using both barycenter and constant weights.

# Author: Alexandre Gramfort <alexandre.gramfort@inria.fr>
#         Fabian Pedregosa <fabian.pedregosa@inria.fr>
#
# License: BSD 3 clause (C) INRIA

Generate sample data¶

import matplotlib.pyplot as plt
import numpy as np

from sklearn import neighbors

np.random.seed(0)
X = np.sort(5 * np.random.rand(40, 1), axis=0)
T = np.linspace(0, 5, 500)[:, np.newaxis]
y = np.sin(X).ravel()

# Add noise to targets
y[::5] += 1 * (0.5 - np.random.rand(8))

Fit regression model¶

n_neighbors = 5

for i, weights in enumerate(["uniform", "distance"]):
    knn = neighbors.KNeighborsRegressor(n_neighbors, weights=weights)
    y_ = knn.fit(X, y).predict(T)

    plt.subplot(2, 1, i + 1)
    plt.scatter(X, y, color="darkorange", label="data")
    plt.plot(T, y_, color="navy", label="prediction")
    plt.axis("tight")
    plt.legend()
    plt.title("KNeighborsRegressor (k = %i, weights = '%s')" % (n_neighbors, weights))

plt.tight_layout()
plt.show()