Note
Go to the end to download the full example code or to run this example in your browser via JupyterLite or Binder
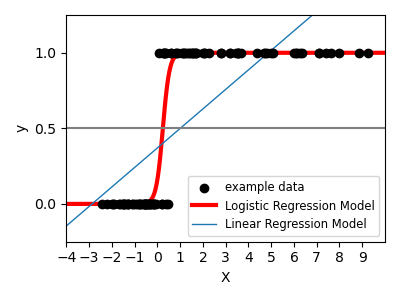
Logistic function¶
Shown in the plot is how the logistic regression would, in this synthetic dataset, classify values as either 0 or 1, i.e. class one or two, using the logistic curve.
# Code source: Gael Varoquaux
# License: BSD 3 clause
import matplotlib.pyplot as plt
import numpy as np
from scipy.special import expit
from sklearn.linear_model import LinearRegression, LogisticRegression
# Generate a toy dataset, it's just a straight line with some Gaussian noise:
xmin, xmax = -5, 5
n_samples = 100
np.random.seed(0)
X = np.random.normal(size=n_samples)
y = (X > 0).astype(float)
X[X > 0] *= 4
X += 0.3 * np.random.normal(size=n_samples)
X = X[:, np.newaxis]
# Fit the classifier
clf = LogisticRegression(C=1e5)
clf.fit(X, y)
# and plot the result
plt.figure(1, figsize=(4, 3))
plt.clf()
plt.scatter(X.ravel(), y, label="example data", color="black", zorder=20)
X_test = np.linspace(-5, 10, 300)
loss = expit(X_test * clf.coef_ + clf.intercept_).ravel()
plt.plot(X_test, loss, label="Logistic Regression Model", color="red", linewidth=3)
ols = LinearRegression()
ols.fit(X, y)
plt.plot(
X_test,
ols.coef_ * X_test + ols.intercept_,
label="Linear Regression Model",
linewidth=1,
)
plt.axhline(0.5, color=".5")
plt.ylabel("y")
plt.xlabel("X")
plt.xticks(range(-5, 10))
plt.yticks([0, 0.5, 1])
plt.ylim(-0.25, 1.25)
plt.xlim(-4, 10)
plt.legend(
loc="lower right",
fontsize="small",
)
plt.tight_layout()
plt.show()
Total running time of the script: (0 minutes 0.109 seconds)
Related examples

Restricted Boltzmann Machine features for digit classification
Restricted Boltzmann Machine features for digit classification
Ordinary Least Squares and Ridge Regression Variance
Ordinary Least Squares and Ridge Regression Variance