A demo of the Spectral Biclustering algorithm

This example demonstrates how to generate a checkerboard dataset and bicluster it using the SpectralBiclustering algorithm. The spectral biclustering algorithm is specifically designed to cluster data by simultaneously considering both the rows (samples) and columns (features) of a matrix. It aims to identify patterns not only between samples but also within subsets of samples, allowing for the detection of localized structure within the data. This makes spectral biclustering particularly well-suited for datasets where the order or arrangement of features is fixed, such as in images, time series, or genomes.

The data is generated, then shuffled and passed to the spectral biclustering algorithm. The rows and columns of the shuffled matrix are then rearranged to plot the biclusters found.

# Author: Kemal Eren <kemal@kemaleren.com>
# License: BSD 3 clause

Generate sample data

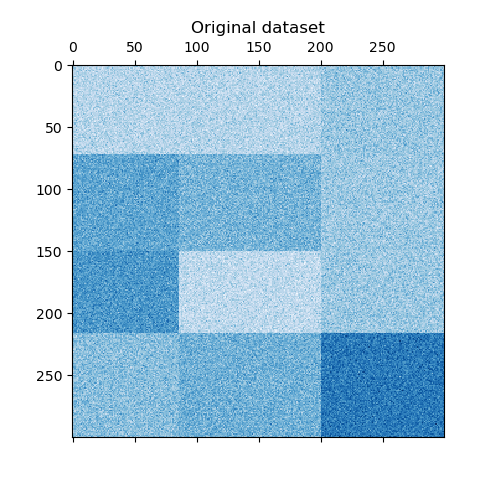
We generate the sample data using the make_checkerboard function. Each pixel within shape=(300, 300) represents with it’s color a value from a uniform distribution. The noise is added from a normal distribution, where the value chosen for noise is the standard deviation.

As you can see, the data is distributed over 12 cluster cells and is relatively well distinguishable.

from matplotlib import pyplot as plt

from sklearn.datasets import make_checkerboard

n_clusters = (4, 3)
data, rows, columns = make_checkerboard(
    shape=(300, 300), n_clusters=n_clusters, noise=10, shuffle=False, random_state=42
)

plt.matshow(data, cmap=plt.cm.Blues)
plt.title("Original dataset")
_ = plt.show()

We shuffle the data and the goal is to reconstruct it afterwards using SpectralBiclustering.

import numpy as np

# Creating lists of shuffled row and column indices
rng = np.random.RandomState(0)
row_idx_shuffled = rng.permutation(data.shape[0])
col_idx_shuffled = rng.permutation(data.shape[1])

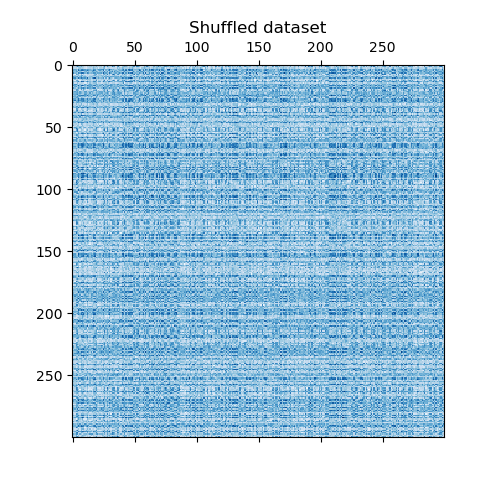
We redefine the shuffled data and plot it. We observe that we lost the structure of original data matrix.

data = data[row_idx_shuffled][:, col_idx_shuffled]

plt.matshow(data, cmap=plt.cm.Blues)
plt.title("Shuffled dataset")
_ = plt.show()

Fitting SpectralBiclustering

We fit the model and compare the obtained clusters with the ground truth. Note that when creating the model we specify the same number of clusters that we used to create the dataset (n_clusters = (4, 3)), which will contribute to obtain a good result.

from sklearn.cluster import SpectralBiclustering
from sklearn.metrics import consensus_score

model = SpectralBiclustering(n_clusters=n_clusters, method="log", random_state=0)
model.fit(data)

# Compute the similarity of two sets of biclusters
score = consensus_score(
    model.biclusters_, (rows[:, row_idx_shuffled], columns[:, col_idx_shuffled])
)
print(f"consensus score: {score:.1f}")

consensus score: 1.0

The score is between 0 and 1, where 1 corresponds to a perfect matching. It shows the quality of the biclustering.

Plotting results

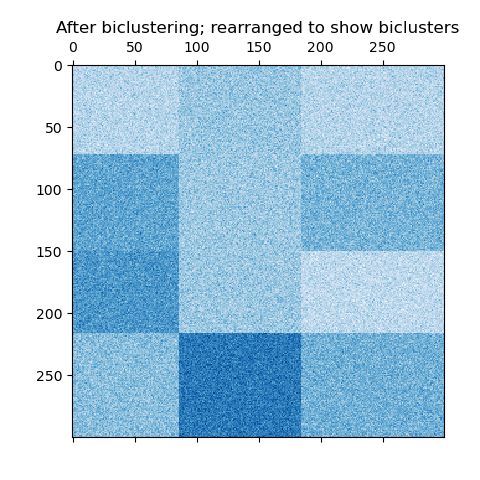
Now, we rearrange the data based on the row and column labels assigned by the SpectralBiclustering model in ascending order and plot again. The row_labels_ range from 0 to 3, while the column_labels_ range from 0 to 2, representing a total of 4 clusters per row and 3 clusters per column.

# Reordering first the rows and then the columns.
reordered_rows = data[np.argsort(model.row_labels_)]
reordered_data = reordered_rows[:, np.argsort(model.column_labels_)]

plt.matshow(reordered_data, cmap=plt.cm.Blues)
plt.title("After biclustering; rearranged to show biclusters")
_ = plt.show()

As a last step, we want to demonstrate the relationships between the row and column labels assigned by the model. Therefore, we create a grid with numpy.outer, which takes the sorted row_labels_ and column_labels_ and adds 1 to each to ensure that the labels start from 1 instead of 0 for better visualization.

plt.matshow(
    np.outer(np.sort(model.row_labels_) + 1, np.sort(model.column_labels_) + 1),
    cmap=plt.cm.Blues,
)
plt.title("Checkerboard structure of rearranged data")
plt.show()

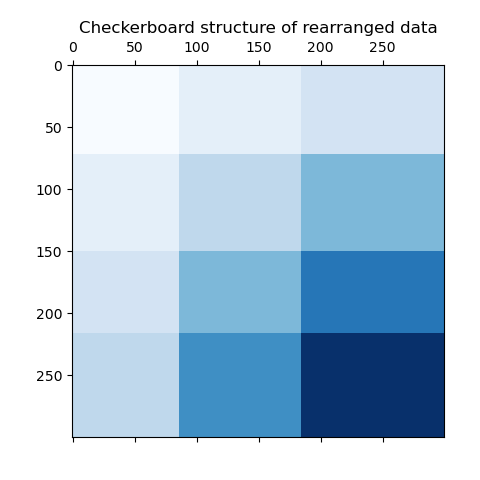
The outer product of the row and column label vectors shows a representation of the checkerboard structure, where different combinations of row and column labels are represented by different shades of blue.