Note
Click here to download the full example code or to run this example in your browser via Binder
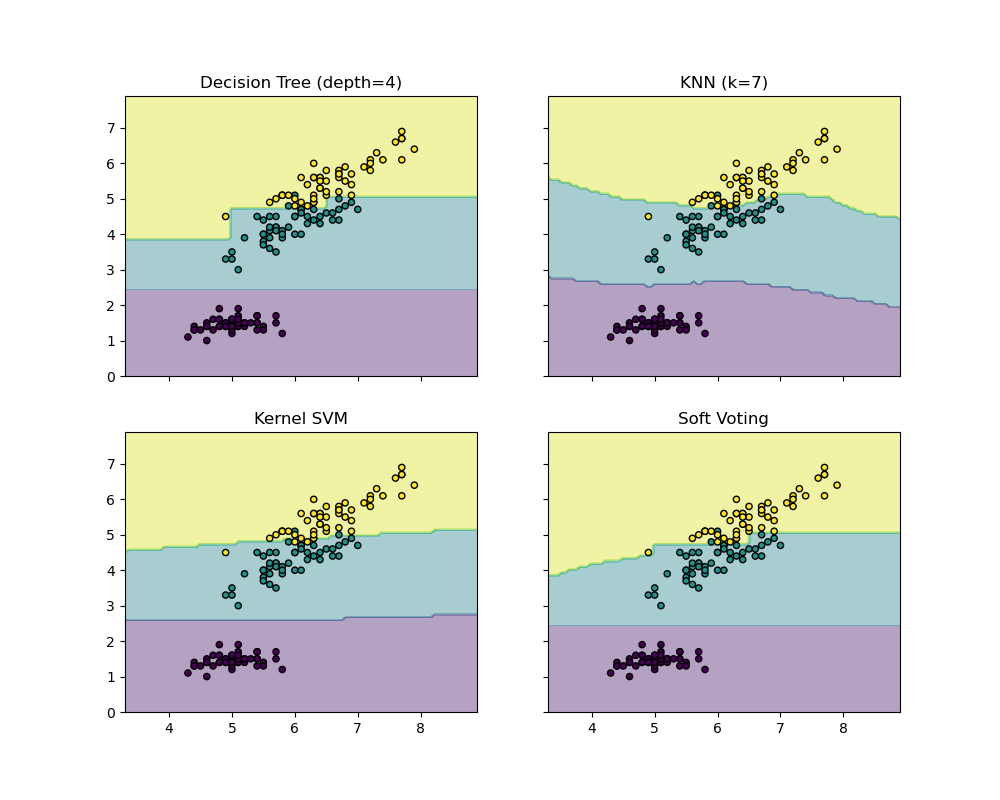
Plot the decision boundaries of a VotingClassifier¶
Plot the decision boundaries of a VotingClassifier for two
features of the Iris dataset.
Plot the class probabilities of the first sample in a toy dataset predicted by
three different classifiers and averaged by the
VotingClassifier.
First, three exemplary classifiers are initialized
(DecisionTreeClassifier,
KNeighborsClassifier, and SVC) and used to
initialize a soft-voting VotingClassifier with weights [2,
1, 2], which means that the predicted probabilities of the
DecisionTreeClassifier and SVC each count 2 times
as much as the weights of the KNeighborsClassifier
classifier when the averaged probability is calculated.
from itertools import product
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.ensemble import VotingClassifier
from sklearn.inspection import DecisionBoundaryDisplay
# Loading some example data
iris = datasets.load_iris()
X = iris.data[:, [0, 2]]
y = iris.target
# Training classifiers
clf1 = DecisionTreeClassifier(max_depth=4)
clf2 = KNeighborsClassifier(n_neighbors=7)
clf3 = SVC(gamma=0.1, kernel="rbf", probability=True)
eclf = VotingClassifier(
estimators=[("dt", clf1), ("knn", clf2), ("svc", clf3)],
voting="soft",
weights=[2, 1, 2],
)
clf1.fit(X, y)
clf2.fit(X, y)
clf3.fit(X, y)
eclf.fit(X, y)
# Plotting decision regions
f, axarr = plt.subplots(2, 2, sharex="col", sharey="row", figsize=(10, 8))
for idx, clf, tt in zip(
product([0, 1], [0, 1]),
[clf1, clf2, clf3, eclf],
["Decision Tree (depth=4)", "KNN (k=7)", "Kernel SVM", "Soft Voting"],
):
DecisionBoundaryDisplay.from_estimator(
clf, X, alpha=0.4, ax=axarr[idx[0], idx[1]], response_method="predict"
)
axarr[idx[0], idx[1]].scatter(X[:, 0], X[:, 1], c=y, s=20, edgecolor="k")
axarr[idx[0], idx[1]].set_title(tt)
plt.show()
Total running time of the script: ( 0 minutes 0.506 seconds)