sklearn.utils.shuffle¶
- sklearn.utils.shuffle(*arrays, random_state=None, n_samples=None)[source]¶
Shuffle arrays or sparse matrices in a consistent way.
This is a convenience alias to
resample(*arrays, replace=False)to do random permutations of the collections.- Parameters:
- *arrayssequence of indexable data-structures
Indexable data-structures can be arrays, lists, dataframes or scipy sparse matrices with consistent first dimension.
- random_stateint, RandomState instance or None, default=None
Determines random number generation for shuffling the data. Pass an int for reproducible results across multiple function calls. See Glossary.
- n_samplesint, default=None
Number of samples to generate. If left to None this is automatically set to the first dimension of the arrays. It should not be larger than the length of arrays.
- Returns:
- shuffled_arrayssequence of indexable data-structures
Sequence of shuffled copies of the collections. The original arrays are not impacted.
See also
Examples
It is possible to mix sparse and dense arrays in the same run:
>>> import numpy as np >>> X = np.array([[1., 0.], [2., 1.], [0., 0.]]) >>> y = np.array([0, 1, 2]) >>> from scipy.sparse import coo_matrix >>> X_sparse = coo_matrix(X) >>> from sklearn.utils import shuffle >>> X, X_sparse, y = shuffle(X, X_sparse, y, random_state=0) >>> X array([[0., 0.], [2., 1.], [1., 0.]]) >>> X_sparse <3x2 sparse matrix of type '<... 'numpy.float64'>' with 3 stored elements in Compressed Sparse Row format> >>> X_sparse.toarray() array([[0., 0.], [2., 1.], [1., 0.]]) >>> y array([2, 1, 0]) >>> shuffle(y, n_samples=2, random_state=0) array([0, 1])
Examples using sklearn.utils.shuffle¶
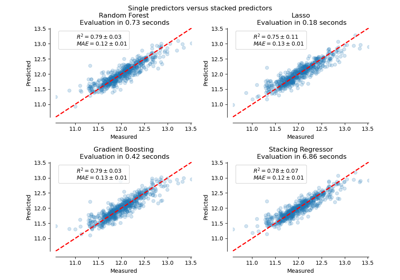
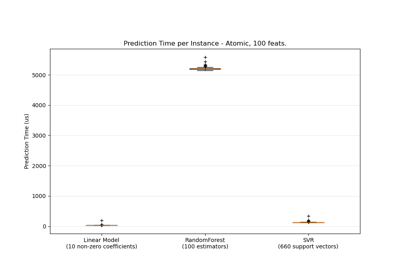
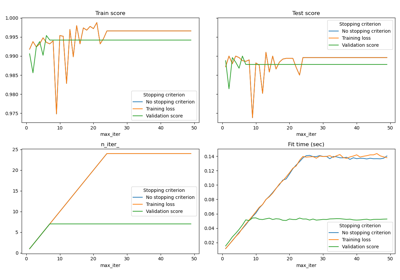
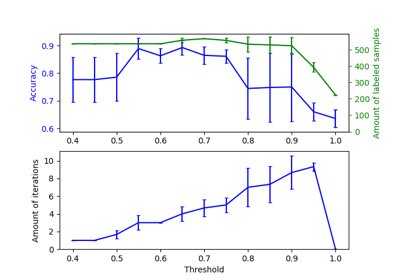
Empirical evaluation of the impact of k-means initialization