sklearn.metrics.v_measure_score

sklearn.metrics.v_measure_score(labels_true, labels_pred, *, beta=1.0)[source]

V-measure cluster labeling given a ground truth.

This score is identical to normalized_mutual_info_score with the 'arithmetic' option for averaging.

The V-measure is the harmonic mean between homogeneity and completeness:

v = (1 + beta) * homogeneity * completeness
     / (beta * homogeneity + completeness)

This metric is independent of the absolute values of the labels: a permutation of the class or cluster label values won’t change the score value in any way.

This metric is furthermore symmetric: switching label_true with label_pred will return the same score value. This can be useful to measure the agreement of two independent label assignments strategies on the same dataset when the real ground truth is not known.

Read more in the User Guide.

Parameters:
labels_trueint array, shape = [n_samples]

ground truth class labels to be used as a reference

labels_predarray-like of shape (n_samples,)

cluster labels to evaluate

betafloat, default=1.0

Ratio of weight attributed to homogeneity vs completeness. If beta is greater than 1, completeness is weighted more strongly in the calculation. If beta is less than 1, homogeneity is weighted more strongly.

Returns:
v_measurefloat

score between 0.0 and 1.0. 1.0 stands for perfectly complete labeling

See also

homogeneity_score
completeness_score
normalized_mutual_info_score

References

Examples

Perfect labelings are both homogeneous and complete, hence have score 1.0:

>>> from sklearn.metrics.cluster import v_measure_score
>>> v_measure_score([0, 0, 1, 1], [0, 0, 1, 1])
1.0
>>> v_measure_score([0, 0, 1, 1], [1, 1, 0, 0])
1.0

Labelings that assign all classes members to the same clusters are complete but not homogeneous, hence penalized:

>>> print("%.6f" % v_measure_score([0, 0, 1, 2], [0, 0, 1, 1]))
0.8...
>>> print("%.6f" % v_measure_score([0, 1, 2, 3], [0, 0, 1, 1]))
0.66...

Labelings that have pure clusters with members coming from the same classes are homogeneous but un-necessary splits harm completeness and thus penalize V-measure as well:

>>> print("%.6f" % v_measure_score([0, 0, 1, 1], [0, 0, 1, 2]))
0.8...
>>> print("%.6f" % v_measure_score([0, 0, 1, 1], [0, 1, 2, 3]))
0.66...

If classes members are completely split across different clusters, the assignment is totally incomplete, hence the V-Measure is null:

>>> print("%.6f" % v_measure_score([0, 0, 0, 0], [0, 1, 2, 3]))
0.0...

Clusters that include samples from totally different classes totally destroy the homogeneity of the labeling, hence:

>>> print("%.6f" % v_measure_score([0, 0, 1, 1], [0, 0, 0, 0]))
0.0...

Examples using sklearn.metrics.v_measure_score

Biclustering documents with the Spectral Co-clustering algorithm

Biclustering documents with the Spectral Co-clustering algorithm

Biclustering documents with the Spectral Co-clustering algorithm
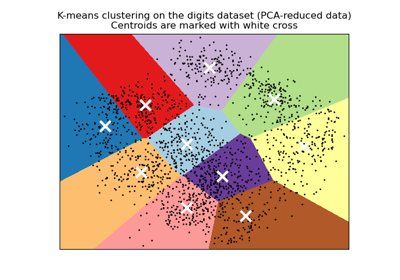
A demo of K-Means clustering on the handwritten digits data

A demo of K-Means clustering on the handwritten digits data

A demo of K-Means clustering on the handwritten digits data
Adjustment for chance in clustering performance evaluation

Adjustment for chance in clustering performance evaluation

Adjustment for chance in clustering performance evaluation
Demo of DBSCAN clustering algorithm

Demo of DBSCAN clustering algorithm

Demo of DBSCAN clustering algorithm
Demo of affinity propagation clustering algorithm

Demo of affinity propagation clustering algorithm

Demo of affinity propagation clustering algorithm
Clustering text documents using k-means

Clustering text documents using k-means

Clustering text documents using k-means