sklearn.manifold.LocallyLinearEmbedding

class sklearn.manifold.LocallyLinearEmbedding(*, n_neighbors=5, n_components=2, reg=0.001, eigen_solver='auto', tol=1e-06, max_iter=100, method='standard', hessian_tol=0.0001, modified_tol=1e-12, neighbors_algorithm='auto', random_state=None, n_jobs=None)

Locally Linear Embedding.

Read more in the User Guide.

Parameters:

n_neighborsint, default=5

Number of neighbors to consider for each point.

n_componentsint, default=2

Number of coordinates for the manifold.

regfloat, default=1e-3

Regularization constant, multiplies the trace of the local covariance matrix of the distances.

eigen_solver{‘auto’, ‘arpack’, ‘dense’}, default=’auto’

The solver used to compute the eigenvectors. The available options are:

• 'auto' : algorithm will attempt to choose the best method for input data.

• 'arpack' : use arnoldi iteration in shift-invert mode. For this method, M may be a dense matrix, sparse matrix, or general linear operator.

• 'dense' : use standard dense matrix operations for the eigenvalue decomposition. For this method, M must be an array or matrix type. This method should be avoided for large problems.

Warning

ARPACK can be unstable for some problems. It is best to try several random seeds in order to check results.

tolfloat, default=1e-6

Tolerance for ‘arpack’ method Not used if eigen_solver==’dense’.

max_iterint, default=100

Maximum number of iterations for the arpack solver. Not used if eigen_solver==’dense’.

method{‘standard’, ‘hessian’, ‘modified’, ‘ltsa’}, default=’standard’

• standard: use the standard locally linear embedding algorithm. see reference [1]

• hessian: use the Hessian eigenmap method. This method requires n_neighbors > n_components * (1 + (n_components + 1) / 2. see reference [2]

• modified: use the modified locally linear embedding algorithm. see reference [3]

• ltsa: use local tangent space alignment algorithm. see reference [4]

hessian_tolfloat, default=1e-4

Tolerance for Hessian eigenmapping method. Only used if method == 'hessian'.

modified_tolfloat, default=1e-12

Tolerance for modified LLE method. Only used if method == 'modified'.

neighbors_algorithm{‘auto’, ‘brute’, ‘kd_tree’, ‘ball_tree’}, default=’auto’

Algorithm to use for nearest neighbors search, passed to NearestNeighbors instance.

random_stateint, RandomState instance, default=None

Determines the random number generator when eigen_solver == ‘arpack’. Pass an int for reproducible results across multiple function calls. See Glossary.

n_jobsint or None, default=None

The number of parallel jobs to run. None means 1 unless in a joblib.parallel_backend context. -1 means using all processors. See Glossary for more details.

Attributes:

embedding_array-like, shape [n_samples, n_components]

Stores the embedding vectors

reconstruction_error_float

Reconstruction error associated with embedding_

n_features_in_int

Number of features seen during fit.

New in version 0.24.

feature_names_in_ndarray of shape (n_features_in_,)

Names of features seen during fit. Defined only when X has feature names that are all strings.

New in version 1.0.

nbrs_NearestNeighbors object

Stores nearest neighbors instance, including BallTree or KDtree if applicable.

See also

SpectralEmbedding

Spectral embedding for non-linear dimensionality reduction.

TSNE

Distributed Stochastic Neighbor Embedding.

References

[1]

Roweis, S. & Saul, L. Nonlinear dimensionality reduction by locally linear embedding. Science 290:2323 (2000).

[2]

Donoho, D. & Grimes, C. Hessian eigenmaps: Locally linear embedding techniques for high-dimensional data. Proc Natl Acad Sci U S A. 100:5591 (2003).

[3]

Zhang, Z. & Wang, J. MLLE: Modified Locally Linear Embedding Using Multiple Weights. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.70.382

[4]

Zhang, Z. & Zha, H. Principal manifolds and nonlinear dimensionality reduction via tangent space alignment. Journal of Shanghai Univ. 8:406 (2004)

Examples

>>> from sklearn.datasets import load_digits
>>> from sklearn.manifold import LocallyLinearEmbedding
>>> X, _ = load_digits(return_X_y=True)
>>> X.shape
(1797, 64)
>>> embedding = LocallyLinearEmbedding(n_components=2)
>>> X_transformed = embedding.fit_transform(X[:100])
>>> X_transformed.shape
(100, 2)

Methods

fit(X[, y])	Compute the embedding vectors for data X.
fit_transform(X[, y])	Compute the embedding vectors for data X and transform X.
get_feature_names_out([input_features])	Get output feature names for transformation.
get_params([deep])	Get parameters for this estimator.
set_params(**params)	Set the parameters of this estimator.
transform(X)	Transform new points into embedding space.

fit(X, y=None)

Compute the embedding vectors for data X.

Parameters:

Xarray-like of shape (n_samples, n_features)

Training set.

yIgnored

Not used, present here for API consistency by convention.

Returns:

selfobject

Fitted LocallyLinearEmbedding class instance.

fit_transform(X, y=None)

Compute the embedding vectors for data X and transform X.

Parameters:

Xarray-like of shape (n_samples, n_features)

Training set.

yIgnored

Not used, present here for API consistency by convention.

Returns:

X_newarray-like, shape (n_samples, n_components)

Returns the instance itself.

get_feature_names_out(input_features=None)

Get output feature names for transformation.

Parameters:

input_featuresarray-like of str or None, default=None

Only used to validate feature names with the names seen in fit.

Returns:

feature_names_outndarray of str objects

Transformed feature names.

get_params(deep=True)

Get parameters for this estimator.

Parameters:

deepbool, default=True

If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

paramsdict

Parameter names mapped to their values.

set_params(**params)

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as Pipeline). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters:

**paramsdict

Estimator parameters.

Returns:

selfestimator instance

Estimator instance.

transform(X)

Transform new points into embedding space.

Parameters:

Xarray-like of shape (n_samples, n_features)

Training set.

Returns:

X_newndarray of shape (n_samples, n_components)

Returns the instance itself.

Notes

Because of scaling performed by this method, it is discouraged to use it together with methods that are not scale-invariant (like SVMs).

Examples using sklearn.manifold.LocallyLinearEmbedding

Visualizing the stock market structure

Visualizing the stock market structure

Comparison of Manifold Learning methods

Comparison of Manifold Learning methods

Manifold Learning methods on a severed sphere

Manifold Learning methods on a severed sphere

Manifold learning on handwritten digits: Locally Linear Embedding, Isomap…

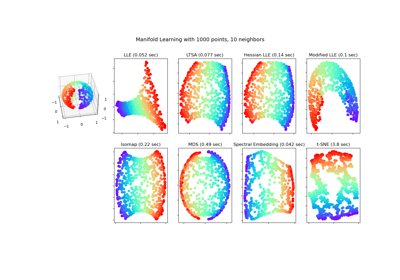
Manifold learning on handwritten digits: Locally Linear Embedding, Isomap...