sklearn.manifold.SpectralEmbedding

class sklearn.manifold.SpectralEmbedding(n_components=2, *, affinity='nearest_neighbors', gamma=None, random_state=None, eigen_solver=None, n_neighbors=None, n_jobs=None)[source]

Spectral embedding for non-linear dimensionality reduction.

Forms an affinity matrix given by the specified function and applies spectral decomposition to the corresponding graph laplacian. The resulting transformation is given by the value of the eigenvectors for each data point.

Note : Laplacian Eigenmaps is the actual algorithm implemented here.

Read more in the User Guide.

Parameters:
n_componentsint, default=2

The dimension of the projected subspace.

affinity{‘nearest_neighbors’, ‘rbf’, ‘precomputed’, ‘precomputed_nearest_neighbors’} or callable, default=’nearest_neighbors’
How to construct the affinity matrix.

  • ‘nearest_neighbors’ : construct the affinity matrix by computing a graph of nearest neighbors.

  • ‘rbf’ : construct the affinity matrix by computing a radial basis function (RBF) kernel.

  • ‘precomputed’ : interpret X as a precomputed affinity matrix.

  • ‘precomputed_nearest_neighbors’ : interpret X as a sparse graph of precomputed nearest neighbors, and constructs the affinity matrix by selecting the n_neighbors nearest neighbors.

  • callable : use passed in function as affinity the function takes in data matrix (n_samples, n_features) and return affinity matrix (n_samples, n_samples).

gammafloat, default=None

Kernel coefficient for rbf kernel. If None, gamma will be set to 1/n_features.

random_stateint, RandomState instance or None, default=None

A pseudo random number generator used for the initialization of the lobpcg eigen vectors decomposition when eigen_solver == 'amg', and for the K-Means initialization. Use an int to make the results deterministic across calls (See Glossary).

Note

When using eigen_solver == 'amg', it is necessary to also fix the global numpy seed with np.random.seed(int) to get deterministic results. See https://github.com/pyamg/pyamg/issues/139 for further information.

eigen_solver{‘arpack’, ‘lobpcg’, ‘amg’}, default=None

The eigenvalue decomposition strategy to use. AMG requires pyamg to be installed. It can be faster on very large, sparse problems. If None, then 'arpack' is used.

n_neighborsint, default=None

Number of nearest neighbors for nearest_neighbors graph building. If None, n_neighbors will be set to max(n_samples/10, 1).

n_jobsint, default=None

The number of parallel jobs to run. None means 1 unless in a joblib.parallel_backend context. -1 means using all processors. See Glossary for more details.

Attributes:
embedding_ndarray of shape (n_samples, n_components)

Spectral embedding of the training matrix.

affinity_matrix_ndarray of shape (n_samples, n_samples)

Affinity_matrix constructed from samples or precomputed.

n_features_in_int

Number of features seen during fit.

New in version 0.24.

feature_names_in_ndarray of shape (n_features_in_,)

Names of features seen during fit. Defined only when X has feature names that are all strings.

New in version 1.0.

n_neighbors_int

Number of nearest neighbors effectively used.

See also

Isomap

Non-linear dimensionality reduction through Isometric Mapping.

References

Examples

>>> from sklearn.datasets import load_digits
>>> from sklearn.manifold import SpectralEmbedding
>>> X, _ = load_digits(return_X_y=True)
>>> X.shape
(1797, 64)
>>> embedding = SpectralEmbedding(n_components=2)
>>> X_transformed = embedding.fit_transform(X[:100])
>>> X_transformed.shape
(100, 2)

Methods

fit(X[, y])

Fit the model from data in X.

fit_transform(X[, y])

Fit the model from data in X and transform X.

get_params([deep])

Get parameters for this estimator.

set_params(**params)

Set the parameters of this estimator.
fit(X, y=None)[source]

Fit the model from data in X.

Parameters:
X{array-like, sparse matrix} of shape (n_samples, n_features)

Training vector, where n_samples is the number of samples and n_features is the number of features.

If affinity is “precomputed” X : {array-like, sparse matrix}, shape (n_samples, n_samples), Interpret X as precomputed adjacency graph computed from samples.

yIgnored

Not used, present for API consistency by convention.

Returns:
selfobject

Returns the instance itself.

fit_transform(X, y=None)[source]

Fit the model from data in X and transform X.

Parameters:
X{array-like, sparse matrix} of shape (n_samples, n_features)

Training vector, where n_samples is the number of samples and n_features is the number of features.

If affinity is “precomputed” X : {array-like, sparse matrix} of shape (n_samples, n_samples), Interpret X as precomputed adjacency graph computed from samples.

yIgnored

Not used, present for API consistency by convention.

Returns:
X_newarray-like of shape (n_samples, n_components)

Spectral embedding of the training matrix.

get_params(deep=True)[source]

Get parameters for this estimator.

Parameters:
deepbool, default=True

If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:
paramsdict

Parameter names mapped to their values.

set_params(**params)[source]

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as Pipeline). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters:
**paramsdict

Estimator parameters.

Returns:
selfestimator instance

Estimator instance.

Examples using sklearn.manifold.SpectralEmbedding

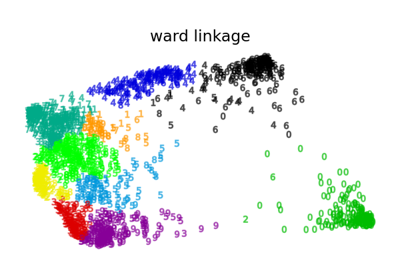
Various Agglomerative Clustering on a 2D embedding of digits

Various Agglomerative Clustering on a 2D embedding of digits

Various Agglomerative Clustering on a 2D embedding of digits
Comparison of Manifold Learning methods

Comparison of Manifold Learning methods

Comparison of Manifold Learning methods
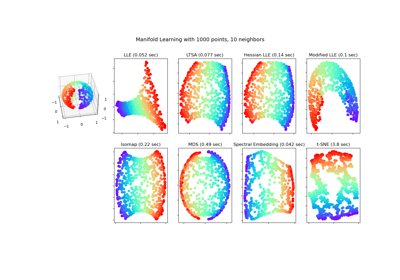
Manifold Learning methods on a severed sphere

Manifold Learning methods on a severed sphere

Manifold Learning methods on a severed sphere
Manifold learning on handwritten digits: Locally Linear Embedding, Isomap...

Manifold learning on handwritten digits: Locally Linear Embedding, Isomap…

Manifold learning on handwritten digits: Locally Linear Embedding, Isomap...