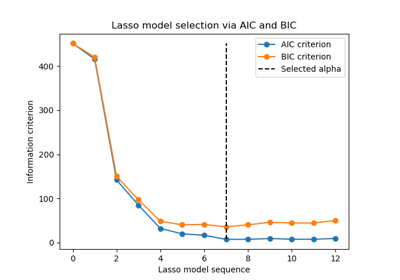
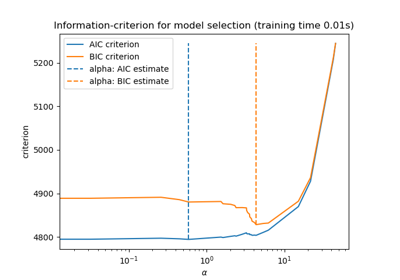
`sklearn.linear_model`.LassoLarsIC¶

class sklearn.linear_model.LassoLarsIC(criterion='aic', *, fit_intercept=True, verbose=False, normalize='deprecated', precompute='auto', max_iter=500, eps=2.220446049250313e-16, copy_X=True, positive=False, noise_variance=None)[source]¶

Lasso model fit with Lars using BIC or AIC for model selection.

The optimization objective for Lasso is:

(1 / (2 * n_samples)) * ||y - Xw||^2_2 + alpha * ||w||_1

AIC is the Akaike information criterion [2] and BIC is the Bayes Information criterion [3]. Such criteria are useful to select the value of the regularization parameter by making a trade-off between the goodness of fit and the complexity of the model. A good model should explain well the data while being simple.

See also

lars_path: Compute Least Angle Regression or Lasso path using LARS algorithm.
lasso_path: Compute Lasso path with coordinate descent.
Lasso: Linear Model trained with L1 prior as regularizer (aka the Lasso).
LassoCV: Lasso linear model with iterative fitting along a regularization path.
LassoLars: Lasso model fit with Least Angle Regression a.k.a. Lars.
LassoLarsCV: Cross-validated Lasso, using the LARS algorithm.
sklearn.decomposition.sparse_encode: Sparse coding.

Notes

The number of degrees of freedom is computed as in [1].

To have more details regarding the mathematical formulation of the AIC and BIC criteria, please refer to User Guide.

References

[1] (1,2)

Zou, Hui, Trevor Hastie, and Robert Tibshirani. “On the degrees of freedom of the lasso.” The Annals of Statistics 35.5 (2007): 2173-2192.

[2]

Wikipedia entry on the Akaike information criterion

[3]

Wikipedia entry on the Bayesian information criterion

Examples

>>> from sklearn import linear_model
>>> reg = linear_model.LassoLarsIC(criterion='bic', normalize=False)
>>> X = [[-2, 2], [-1, 1], [0, 0], [1, 1], [2, 2]]
>>> y = [-2.2222, -1.1111, 0, -1.1111, -2.2222]
>>> reg.fit(X, y)
LassoLarsIC(criterion='bic', normalize=False)
>>> print(reg.coef_)
[ 0.  -1.11...]

Methods

`fit`(X, y[, copy_X])	Fit the model using X, y as training data.
`get_params`([deep])	Get parameters for this estimator.
`predict`(X)	Predict using the linear model.
`score`(X, y[, sample_weight])	Return the coefficient of determination of the prediction.
`set_params`(**params)	Set the parameters of this estimator.

fit(X, y, copy_X=None)[source]¶

Fit the model using X, y as training data.

Parameters:

Xarray-like of shape (n_samples, n_features): Training data.
yarray-like of shape (n_samples,): Target values. Will be cast to X’s dtype if necessary.
copy_Xbool, default=None: If provided, this parameter will override the choice of copy_X made at instance creation. If True, X will be copied; else, it may be overwritten.

Returns:

selfobject: Returns an instance of self.

get_params(deep=True)[source]¶

Get parameters for this estimator.

Parameters:

deepbool, default=True: If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

paramsdict: Parameter names mapped to their values.

predict(X)[source]¶

Predict using the linear model.

Parameters:

Xarray-like or sparse matrix, shape (n_samples, n_features): Samples.

Returns:

Carray, shape (n_samples,): Returns predicted values.

score(X, y, sample_weight=None)[source]¶

Return the coefficient of determination of the prediction.

The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares ((y_true - y_pred)** 2).sum() and \(v\) is the total sum of squares ((y_true - y_true.mean()) ** 2).sum(). The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of y, disregarding the input features, would get a \(R^2\) score of 0.0.

Parameters:

Xarray-like of shape (n_samples, n_features): Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape (n_samples, n_samples_fitted), where n_samples_fitted is the number of samples used in the fitting for the estimator.
yarray-like of shape (n_samples,) or (n_samples, n_outputs): True values for X.
sample_weightarray-like of shape (n_samples,), default=None: Sample weights.

Returns:

scorefloat: \(R^2\) of self.predict(X) wrt. y.

Notes

The \(R^2\) score used when calling score on a regressor uses multioutput='uniform_average' from version 0.23 to keep consistent with default value of r2_score. This influences the score method of all the multioutput regressors (except for MultiOutputRegressor).

set_params(**params)[source]¶

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as Pipeline). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters:

**paramsdict: Estimator parameters.

Returns:

selfestimator instance: Estimator instance.

Examples using `sklearn.linear_model.LassoLarsIC`¶

Lasso model selection via information criteria

Lasso model selection: AIC-BIC / cross-validation

sklearn.linear_model.LassoLarsIC¶

Examples using sklearn.linear_model.LassoLarsIC¶

`sklearn.linear_model`.LassoLarsIC¶

Examples using `sklearn.linear_model.LassoLarsIC`¶