sklearn.gaussian_process.GaussianProcessClassifier¶
- class sklearn.gaussian_process.GaussianProcessClassifier(kernel=None, *, optimizer='fmin_l_bfgs_b', n_restarts_optimizer=0, max_iter_predict=100, warm_start=False, copy_X_train=True, random_state=None, multi_class='one_vs_rest', n_jobs=None)[source]¶
Gaussian process classification (GPC) based on Laplace approximation.
The implementation is based on Algorithm 3.1, 3.2, and 5.1 of Gaussian Processes for Machine Learning (GPML) by Rasmussen and Williams.
Internally, the Laplace approximation is used for approximating the non-Gaussian posterior by a Gaussian.
Currently, the implementation is restricted to using the logistic link function. For multi-class classification, several binary one-versus rest classifiers are fitted. Note that this class thus does not implement a true multi-class Laplace approximation.
Read more in the User Guide.
New in version 0.18.
- Parameters:
- kernelkernel instance, default=None
The kernel specifying the covariance function of the GP. If None is passed, the kernel “1.0 * RBF(1.0)” is used as default. Note that the kernel’s hyperparameters are optimized during fitting. Also kernel cannot be a
CompoundKernel.- optimizer‘fmin_l_bfgs_b’ or callable, default=’fmin_l_bfgs_b’
Can either be one of the internally supported optimizers for optimizing the kernel’s parameters, specified by a string, or an externally defined optimizer passed as a callable. If a callable is passed, it must have the signature:
def optimizer(obj_func, initial_theta, bounds): # * 'obj_func' is the objective function to be maximized, which # takes the hyperparameters theta as parameter and an # optional flag eval_gradient, which determines if the # gradient is returned additionally to the function value # * 'initial_theta': the initial value for theta, which can be # used by local optimizers # * 'bounds': the bounds on the values of theta .... # Returned are the best found hyperparameters theta and # the corresponding value of the target function. return theta_opt, func_min
Per default, the ‘L-BFGS-B’ algorithm from scipy.optimize.minimize is used. If None is passed, the kernel’s parameters are kept fixed. Available internal optimizers are:
'fmin_l_bfgs_b'- n_restarts_optimizerint, default=0
The number of restarts of the optimizer for finding the kernel’s parameters which maximize the log-marginal likelihood. The first run of the optimizer is performed from the kernel’s initial parameters, the remaining ones (if any) from thetas sampled log-uniform randomly from the space of allowed theta-values. If greater than 0, all bounds must be finite. Note that n_restarts_optimizer=0 implies that one run is performed.
- max_iter_predictint, default=100
The maximum number of iterations in Newton’s method for approximating the posterior during predict. Smaller values will reduce computation time at the cost of worse results.
- warm_startbool, default=False
If warm-starts are enabled, the solution of the last Newton iteration on the Laplace approximation of the posterior mode is used as initialization for the next call of _posterior_mode(). This can speed up convergence when _posterior_mode is called several times on similar problems as in hyperparameter optimization. See the Glossary.
- copy_X_trainbool, default=True
If True, a persistent copy of the training data is stored in the object. Otherwise, just a reference to the training data is stored, which might cause predictions to change if the data is modified externally.
- random_stateint, RandomState instance or None, default=None
Determines random number generation used to initialize the centers. Pass an int for reproducible results across multiple function calls. See Glossary.
- multi_class{‘one_vs_rest’, ‘one_vs_one’}, default=’one_vs_rest’
Specifies how multi-class classification problems are handled. Supported are ‘one_vs_rest’ and ‘one_vs_one’. In ‘one_vs_rest’, one binary Gaussian process classifier is fitted for each class, which is trained to separate this class from the rest. In ‘one_vs_one’, one binary Gaussian process classifier is fitted for each pair of classes, which is trained to separate these two classes. The predictions of these binary predictors are combined into multi-class predictions. Note that ‘one_vs_one’ does not support predicting probability estimates.
- n_jobsint, default=None
The number of jobs to use for the computation: the specified multiclass problems are computed in parallel.
Nonemeans 1 unless in ajoblib.parallel_backendcontext.-1means using all processors. See Glossary for more details.
- Attributes:
- base_estimator_
Estimatorinstance The estimator instance that defines the likelihood function using the observed data.
kernel_kernel instanceReturn the kernel of the base estimator.
- log_marginal_likelihood_value_float
The log-marginal-likelihood of
self.kernel_.theta- classes_array-like of shape (n_classes,)
Unique class labels.
- n_classes_int
The number of classes in the training data
- n_features_in_int
Number of features seen during fit.
New in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.New in version 1.0.
- base_estimator_
See also
GaussianProcessRegressorGaussian process regression (GPR).
Examples
>>> from sklearn.datasets import load_iris >>> from sklearn.gaussian_process import GaussianProcessClassifier >>> from sklearn.gaussian_process.kernels import RBF >>> X, y = load_iris(return_X_y=True) >>> kernel = 1.0 * RBF(1.0) >>> gpc = GaussianProcessClassifier(kernel=kernel, ... random_state=0).fit(X, y) >>> gpc.score(X, y) 0.9866... >>> gpc.predict_proba(X[:2,:]) array([[0.83548752, 0.03228706, 0.13222543], [0.79064206, 0.06525643, 0.14410151]])
Methods
fit(X, y)Fit Gaussian process classification model.
get_params([deep])Get parameters for this estimator.
log_marginal_likelihood([theta, ...])Return log-marginal likelihood of theta for training data.
predict(X)Perform classification on an array of test vectors X.
Return probability estimates for the test vector X.
score(X, y[, sample_weight])Return the mean accuracy on the given test data and labels.
set_params(**params)Set the parameters of this estimator.
- fit(X, y)[source]¶
Fit Gaussian process classification model.
- Parameters:
- Xarray-like of shape (n_samples, n_features) or list of object
Feature vectors or other representations of training data.
- yarray-like of shape (n_samples,)
Target values, must be binary.
- Returns:
- selfobject
Returns an instance of self.
- get_params(deep=True)[source]¶
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- property kernel_¶
Return the kernel of the base estimator.
- log_marginal_likelihood(theta=None, eval_gradient=False, clone_kernel=True)[source]¶
Return log-marginal likelihood of theta for training data.
In the case of multi-class classification, the mean log-marginal likelihood of the one-versus-rest classifiers are returned.
- Parameters:
- thetaarray-like of shape (n_kernel_params,), default=None
Kernel hyperparameters for which the log-marginal likelihood is evaluated. In the case of multi-class classification, theta may be the hyperparameters of the compound kernel or of an individual kernel. In the latter case, all individual kernel get assigned the same theta values. If None, the precomputed log_marginal_likelihood of
self.kernel_.thetais returned.- eval_gradientbool, default=False
If True, the gradient of the log-marginal likelihood with respect to the kernel hyperparameters at position theta is returned additionally. Note that gradient computation is not supported for non-binary classification. If True, theta must not be None.
- clone_kernelbool, default=True
If True, the kernel attribute is copied. If False, the kernel attribute is modified, but may result in a performance improvement.
- Returns:
- log_likelihoodfloat
Log-marginal likelihood of theta for training data.
- log_likelihood_gradientndarray of shape (n_kernel_params,), optional
Gradient of the log-marginal likelihood with respect to the kernel hyperparameters at position theta. Only returned when
eval_gradientis True.
- predict(X)[source]¶
Perform classification on an array of test vectors X.
- Parameters:
- Xarray-like of shape (n_samples, n_features) or list of object
Query points where the GP is evaluated for classification.
- Returns:
- Cndarray of shape (n_samples,)
Predicted target values for X, values are from
classes_.
- predict_proba(X)[source]¶
Return probability estimates for the test vector X.
- Parameters:
- Xarray-like of shape (n_samples, n_features) or list of object
Query points where the GP is evaluated for classification.
- Returns:
- Carray-like of shape (n_samples, n_classes)
Returns the probability of the samples for each class in the model. The columns correspond to the classes in sorted order, as they appear in the attribute classes_.
- score(X, y, sample_weight=None)[source]¶
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
Test samples.
- yarray-like of shape (n_samples,) or (n_samples, n_outputs)
True labels for
X.- sample_weightarray-like of shape (n_samples,), default=None
Sample weights.
- Returns:
- scorefloat
Mean accuracy of
self.predict(X)wrt.y.
- set_params(**params)[source]¶
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
Examples using sklearn.gaussian_process.GaussianProcessClassifier¶
Gaussian process classification (GPC) on iris dataset
Illustration of Gaussian process classification (GPC) on the XOR dataset
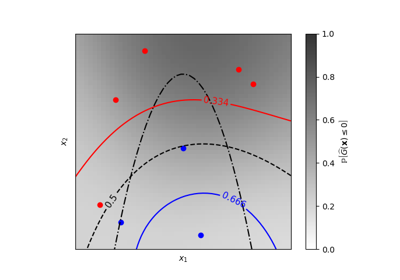
Iso-probability lines for Gaussian Processes classification (GPC)
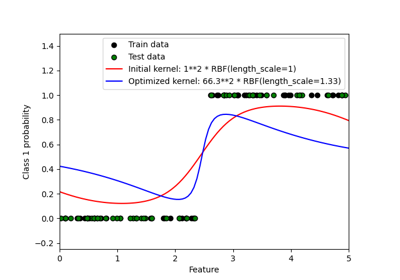
Probabilistic predictions with Gaussian process classification (GPC)