sklearn.ensemble.HistGradientBoostingRegressor¶
- class sklearn.ensemble.HistGradientBoostingRegressor(loss='squared_error', *, quantile=None, learning_rate=0.1, max_iter=100, max_leaf_nodes=31, max_depth=None, min_samples_leaf=20, l2_regularization=0.0, max_bins=255, categorical_features=None, monotonic_cst=None, warm_start=False, early_stopping='auto', scoring='loss', validation_fraction=0.1, n_iter_no_change=10, tol=1e-07, verbose=0, random_state=None)[source]¶
Histogram-based Gradient Boosting Regression Tree.
This estimator is much faster than
GradientBoostingRegressorfor big datasets (n_samples >= 10 000).This estimator has native support for missing values (NaNs). During training, the tree grower learns at each split point whether samples with missing values should go to the left or right child, based on the potential gain. When predicting, samples with missing values are assigned to the left or right child consequently. If no missing values were encountered for a given feature during training, then samples with missing values are mapped to whichever child has the most samples.
This implementation is inspired by LightGBM.
Read more in the User Guide.
New in version 0.21.
- Parameters:
- loss{‘squared_error’, ‘absolute_error’, ‘poisson’, ‘quantile’}, default=’squared_error’
The loss function to use in the boosting process. Note that the “squared error” and “poisson” losses actually implement “half least squares loss” and “half poisson deviance” to simplify the computation of the gradient. Furthermore, “poisson” loss internally uses a log-link and requires
y >= 0. “quantile” uses the pinball loss.Changed in version 0.23: Added option ‘poisson’.
Changed in version 1.1: Added option ‘quantile’.
Deprecated since version 1.0: The loss ‘least_squares’ was deprecated in v1.0 and will be removed in version 1.2. Use
loss='squared_error'which is equivalent.Deprecated since version 1.0: The loss ‘least_absolute_deviation’ was deprecated in v1.0 and will be removed in version 1.2. Use
loss='absolute_error'which is equivalent.- quantilefloat, default=None
If loss is “quantile”, this parameter specifies which quantile to be estimated and must be between 0 and 1.
- learning_ratefloat, default=0.1
The learning rate, also known as shrinkage. This is used as a multiplicative factor for the leaves values. Use
1for no shrinkage.- max_iterint, default=100
The maximum number of iterations of the boosting process, i.e. the maximum number of trees.
- max_leaf_nodesint or None, default=31
The maximum number of leaves for each tree. Must be strictly greater than 1. If None, there is no maximum limit.
- max_depthint or None, default=None
The maximum depth of each tree. The depth of a tree is the number of edges to go from the root to the deepest leaf. Depth isn’t constrained by default.
- min_samples_leafint, default=20
The minimum number of samples per leaf. For small datasets with less than a few hundred samples, it is recommended to lower this value since only very shallow trees would be built.
- l2_regularizationfloat, default=0
The L2 regularization parameter. Use
0for no regularization (default).- max_binsint, default=255
The maximum number of bins to use for non-missing values. Before training, each feature of the input array
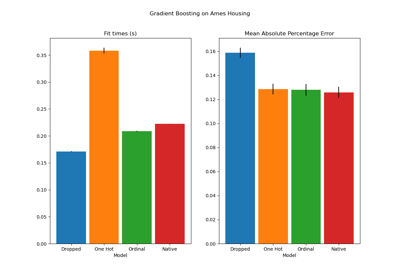
Xis binned into integer-valued bins, which allows for a much faster training stage. Features with a small number of unique values may use less thanmax_binsbins. In addition to themax_binsbins, one more bin is always reserved for missing values. Must be no larger than 255.- categorical_featuresarray-like of {bool, int} of shape (n_features) or shape (n_categorical_features,), default=None
Indicates the categorical features.
None : no feature will be considered categorical.
boolean array-like : boolean mask indicating categorical features.
integer array-like : integer indices indicating categorical features.
For each categorical feature, there must be at most
max_binsunique categories, and each categorical value must be in [0, max_bins -1].Read more in the User Guide.
New in version 0.24.
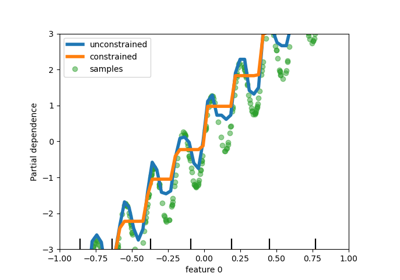
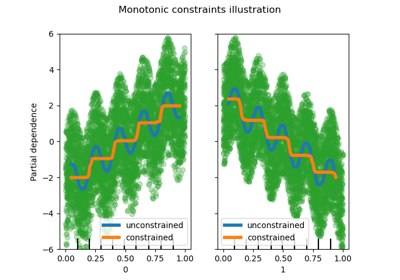
- monotonic_cstarray-like of int of shape (n_features), default=None
Indicates the monotonic constraint to enforce on each feature. -1, 1 and 0 respectively correspond to a negative constraint, positive constraint and no constraint. Read more in the User Guide.
New in version 0.23.
- warm_startbool, default=False
When set to
True, reuse the solution of the previous call to fit and add more estimators to the ensemble. For results to be valid, the estimator should be re-trained on the same data only. See the Glossary.- early_stopping‘auto’ or bool, default=’auto’
If ‘auto’, early stopping is enabled if the sample size is larger than 10000. If True, early stopping is enabled, otherwise early stopping is disabled.
New in version 0.23.
- scoringstr or callable or None, default=’loss’
Scoring parameter to use for early stopping. It can be a single string (see The scoring parameter: defining model evaluation rules) or a callable (see Defining your scoring strategy from metric functions). If None, the estimator’s default scorer is used. If
scoring='loss', early stopping is checked w.r.t the loss value. Only used if early stopping is performed.- validation_fractionint or float or None, default=0.1
Proportion (or absolute size) of training data to set aside as validation data for early stopping. If None, early stopping is done on the training data. Only used if early stopping is performed.
- n_iter_no_changeint, default=10
Used to determine when to “early stop”. The fitting process is stopped when none of the last
n_iter_no_changescores are better than then_iter_no_change - 1-th-to-last one, up to some tolerance. Only used if early stopping is performed.- tolfloat, default=1e-7
The absolute tolerance to use when comparing scores during early stopping. The higher the tolerance, the more likely we are to early stop: higher tolerance means that it will be harder for subsequent iterations to be considered an improvement upon the reference score.
- verboseint, default=0
The verbosity level. If not zero, print some information about the fitting process.
- random_stateint, RandomState instance or None, default=None
Pseudo-random number generator to control the subsampling in the binning process, and the train/validation data split if early stopping is enabled. Pass an int for reproducible output across multiple function calls. See Glossary.
- Attributes:
- do_early_stopping_bool
Indicates whether early stopping is used during training.
n_iter_intNumber of iterations of the boosting process.
- n_trees_per_iteration_int
The number of tree that are built at each iteration. For regressors, this is always 1.
- train_score_ndarray, shape (n_iter_+1,)
The scores at each iteration on the training data. The first entry is the score of the ensemble before the first iteration. Scores are computed according to the
scoringparameter. Ifscoringis not ‘loss’, scores are computed on a subset of at most 10 000 samples. Empty if no early stopping.- validation_score_ndarray, shape (n_iter_+1,)
The scores at each iteration on the held-out validation data. The first entry is the score of the ensemble before the first iteration. Scores are computed according to the
scoringparameter. Empty if no early stopping or ifvalidation_fractionis None.- is_categorical_ndarray, shape (n_features, ) or None
Boolean mask for the categorical features.
Noneif there are no categorical features.- n_features_in_int
Number of features seen during fit.
New in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) Names of features seen during fit. Defined only when
Xhas feature names that are all strings.New in version 1.0.
See also
GradientBoostingRegressorExact gradient boosting method that does not scale as good on datasets with a large number of samples.
sklearn.tree.DecisionTreeRegressorA decision tree regressor.
RandomForestRegressorA meta-estimator that fits a number of decision tree regressors on various sub-samples of the dataset and uses averaging to improve the statistical performance and control over-fitting.
AdaBoostRegressorA meta-estimator that begins by fitting a regressor on the original dataset and then fits additional copies of the regressor on the same dataset but where the weights of instances are adjusted according to the error of the current prediction. As such, subsequent regressors focus more on difficult cases.
Examples
>>> from sklearn.ensemble import HistGradientBoostingRegressor >>> from sklearn.datasets import load_diabetes >>> X, y = load_diabetes(return_X_y=True) >>> est = HistGradientBoostingRegressor().fit(X, y) >>> est.score(X, y) 0.92...
Methods
fit(X, y[, sample_weight])Fit the gradient boosting model.
get_params([deep])Get parameters for this estimator.
predict(X)Predict values for X.
score(X, y[, sample_weight])Return the coefficient of determination of the prediction.
set_params(**params)Set the parameters of this estimator.
Predict regression target for each iteration.
- fit(X, y, sample_weight=None)[source]¶
Fit the gradient boosting model.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
The input samples.
- yarray-like of shape (n_samples,)
Target values.
- sample_weightarray-like of shape (n_samples,) default=None
Weights of training data.
New in version 0.23.
- Returns:
- selfobject
Fitted estimator.
- get_params(deep=True)[source]¶
Get parameters for this estimator.
- Parameters:
- deepbool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
- Returns:
- paramsdict
Parameter names mapped to their values.
- property n_iter_¶
Number of iterations of the boosting process.
- predict(X)[source]¶
Predict values for X.
- Parameters:
- Xarray-like, shape (n_samples, n_features)
The input samples.
- Returns:
- yndarray, shape (n_samples,)
The predicted values.
- score(X, y, sample_weight=None)[source]¶
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares
((y_true - y_pred)** 2).sum()and \(v\) is the total sum of squares((y_true - y_true.mean()) ** 2).sum(). The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value ofy, disregarding the input features, would get a \(R^2\) score of 0.0.- Parameters:
- Xarray-like of shape (n_samples, n_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape
(n_samples, n_samples_fitted), wheren_samples_fittedis the number of samples used in the fitting for the estimator.- yarray-like of shape (n_samples,) or (n_samples, n_outputs)
True values for
X.- sample_weightarray-like of shape (n_samples,), default=None
Sample weights.
- Returns:
- scorefloat
\(R^2\) of
self.predict(X)wrt.y.
Notes
The \(R^2\) score used when calling
scoreon a regressor usesmultioutput='uniform_average'from version 0.23 to keep consistent with default value ofr2_score. This influences thescoremethod of all the multioutput regressors (except forMultiOutputRegressor).
- set_params(**params)[source]¶
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as
Pipeline). The latter have parameters of the form<component>__<parameter>so that it’s possible to update each component of a nested object.- Parameters:
- **paramsdict
Estimator parameters.
- Returns:
- selfestimator instance
Estimator instance.
- staged_predict(X)[source]¶
Predict regression target for each iteration.
This method allows monitoring (i.e. determine error on testing set) after each stage.
New in version 0.24.
- Parameters:
- Xarray-like of shape (n_samples, n_features)
The input samples.
- Yields:
- ygenerator of ndarray of shape (n_samples,)
The predicted values of the input samples, for each iteration.
Examples using sklearn.ensemble.HistGradientBoostingRegressor¶
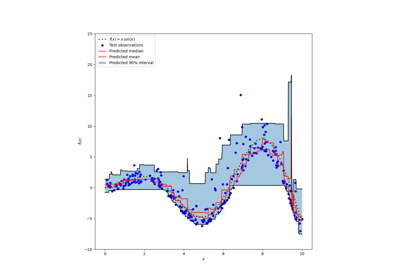
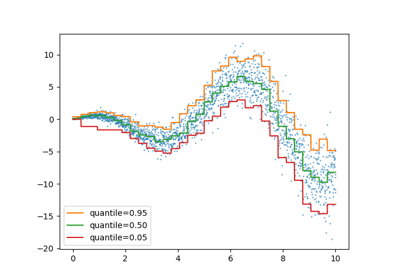
Prediction Intervals for Gradient Boosting Regression
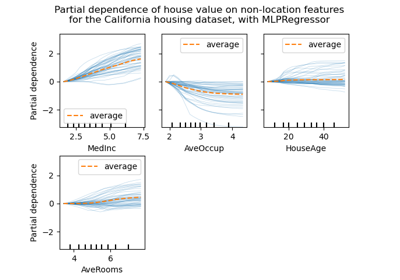
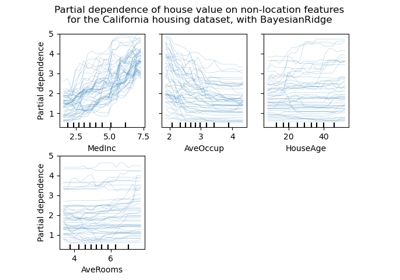
Partial Dependence and Individual Conditional Expectation Plots