sklearn.discriminant_analysis.LinearDiscriminantAnalysis

class sklearn.discriminant_analysis.LinearDiscriminantAnalysis(solver='svd', shrinkage=None, priors=None, n_components=None, store_covariance=False, tol=0.0001, covariance_estimator=None)

Linear Discriminant Analysis.

A classifier with a linear decision boundary, generated by fitting class conditional densities to the data and using Bayes’ rule.

The model fits a Gaussian density to each class, assuming that all classes share the same covariance matrix.

The fitted model can also be used to reduce the dimensionality of the input by projecting it to the most discriminative directions, using the transform method.

New in version 0.17: LinearDiscriminantAnalysis.

Read more in the User Guide.

Parameters:

solver{‘svd’, ‘lsqr’, ‘eigen’}, default=’svd’

Solver to use, possible values:

• ‘svd’: Singular value decomposition (default). Does not compute the covariance matrix, therefore this solver is recommended for data with a large number of features.

• ‘lsqr’: Least squares solution. Can be combined with shrinkage or custom covariance estimator.

• ‘eigen’: Eigenvalue decomposition. Can be combined with shrinkage or custom covariance estimator.

shrinkage‘auto’ or float, default=None

Shrinkage parameter, possible values:

• None: no shrinkage (default).

• ‘auto’: automatic shrinkage using the Ledoit-Wolf lemma.

• float between 0 and 1: fixed shrinkage parameter.

This should be left to None if covariance_estimator is used. Note that shrinkage works only with ‘lsqr’ and ‘eigen’ solvers.

priorsarray-like of shape (n_classes,), default=None

The class prior probabilities. By default, the class proportions are inferred from the training data.

n_componentsint, default=None

Number of components (<= min(n_classes - 1, n_features)) for dimensionality reduction. If None, will be set to min(n_classes - 1, n_features). This parameter only affects the transform method.

store_covariancebool, default=False

If True, explicitly compute the weighted within-class covariance matrix when solver is ‘svd’. The matrix is always computed and stored for the other solvers.

New in version 0.17.

tolfloat, default=1.0e-4

Absolute threshold for a singular value of X to be considered significant, used to estimate the rank of X. Dimensions whose singular values are non-significant are discarded. Only used if solver is ‘svd’.

New in version 0.17.

covariance_estimatorcovariance estimator, default=None

If not None, covariance_estimator is used to estimate the covariance matrices instead of relying on the empirical covariance estimator (with potential shrinkage). The object should have a fit method and a covariance_ attribute like the estimators in sklearn.covariance. if None the shrinkage parameter drives the estimate.

This should be left to None if shrinkage is used. Note that covariance_estimator works only with ‘lsqr’ and ‘eigen’ solvers.

New in version 0.24.

Attributes:

coef_ndarray of shape (n_features,) or (n_classes, n_features)

Weight vector(s).

intercept_ndarray of shape (n_classes,)

Intercept term.

covariance_array-like of shape (n_features, n_features)

Weighted within-class covariance matrix. It corresponds to sum_k prior_k * C_k where C_k is the covariance matrix of the samples in class k. The C_k are estimated using the (potentially shrunk) biased estimator of covariance. If solver is ‘svd’, only exists when store_covariance is True.

explained_variance_ratio_ndarray of shape (n_components,)

Percentage of variance explained by each of the selected components. If n_components is not set then all components are stored and the sum of explained variances is equal to 1.0. Only available when eigen or svd solver is used.

means_array-like of shape (n_classes, n_features)

Class-wise means.

priors_array-like of shape (n_classes,)

Class priors (sum to 1).

scalings_array-like of shape (rank, n_classes - 1)

Scaling of the features in the space spanned by the class centroids. Only available for ‘svd’ and ‘eigen’ solvers.

xbar_array-like of shape (n_features,)

Overall mean. Only present if solver is ‘svd’.

classes_array-like of shape (n_classes,)

Unique class labels.

n_features_in_int

Number of features seen during fit.

New in version 0.24.

feature_names_in_ndarray of shape (n_features_in_,)

Names of features seen during fit. Defined only when X has feature names that are all strings.

New in version 1.0.

See also

QuadraticDiscriminantAnalysis

Quadratic Discriminant Analysis.

Examples

>>> import numpy as np
>>> from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> y = np.array([1, 1, 1, 2, 2, 2])
>>> clf = LinearDiscriminantAnalysis()
>>> clf.fit(X, y)
LinearDiscriminantAnalysis()
>>> print(clf.predict([[-0.8, -1]]))
[1]

Methods

decision_function(X)	Apply decision function to an array of samples.
fit(X, y)	Fit the Linear Discriminant Analysis model.
fit_transform(X[, y])	Fit to data, then transform it.
get_feature_names_out([input_features])	Get output feature names for transformation.
get_params([deep])	Get parameters for this estimator.
predict(X)	Predict class labels for samples in X.
predict_log_proba(X)	Estimate log probability.
predict_proba(X)	Estimate probability.
score(X, y[, sample_weight])	Return the mean accuracy on the given test data and labels.
set_params(**params)	Set the parameters of this estimator.
transform(X)	Project data to maximize class separation.

decision_function(X)

Apply decision function to an array of samples.

The decision function is equal (up to a constant factor) to the log-posterior of the model, i.e. log p(y = k | x). In a binary classification setting this instead corresponds to the difference log p(y = 1 | x) - log p(y = 0 | x). See Mathematical formulation of the LDA and QDA classifiers.

Parameters:

Xarray-like of shape (n_samples, n_features)

Array of samples (test vectors).

Returns:

Cndarray of shape (n_samples,) or (n_samples, n_classes)

Decision function values related to each class, per sample. In the two-class case, the shape is (n_samples,), giving the log likelihood ratio of the positive class.

fit(X, y)

Fit the Linear Discriminant Analysis model.

Changed in version 0.19: store_covariance has been moved to main constructor.

Changed in version 0.19: tol has been moved to main constructor.

Parameters:

Xarray-like of shape (n_samples, n_features)

Training data.

yarray-like of shape (n_samples,)

Target values.

Returns:

selfobject

Fitted estimator.

fit_transform(X, y=None, **fit_params)

Fit to data, then transform it.

Fits transformer to X and y with optional parameters fit_params and returns a transformed version of X.

Parameters:

Xarray-like of shape (n_samples, n_features)

Input samples.

yarray-like of shape (n_samples,) or (n_samples, n_outputs), default=None

Target values (None for unsupervised transformations).

**fit_paramsdict

Additional fit parameters.

Returns:

X_newndarray array of shape (n_samples, n_features_new)

Transformed array.

get_feature_names_out(input_features=None)

Get output feature names for transformation.

Parameters:

input_featuresarray-like of str or None, default=None

Only used to validate feature names with the names seen in fit.

Returns:

feature_names_outndarray of str objects

Transformed feature names.

get_params(deep=True)

Get parameters for this estimator.

Parameters:

deepbool, default=True

If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

paramsdict

Parameter names mapped to their values.

predict(X)

Predict class labels for samples in X.

Parameters:

X{array-like, sparse matrix} of shape (n_samples, n_features)

The data matrix for which we want to get the predictions.

Returns:

y_predndarray of shape (n_samples,)

Vector containing the class labels for each sample.

predict_log_proba(X)

Estimate log probability.

Parameters:

Xarray-like of shape (n_samples, n_features)

Input data.

Returns:

Cndarray of shape (n_samples, n_classes)

Estimated log probabilities.

predict_proba(X)

Estimate probability.

Parameters:

Xarray-like of shape (n_samples, n_features)

Input data.

Returns:

Cndarray of shape (n_samples, n_classes)

Estimated probabilities.

score(X, y, sample_weight=None)

Return the mean accuracy on the given test data and labels.

In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.

Parameters:

Xarray-like of shape (n_samples, n_features)

Test samples.

yarray-like of shape (n_samples,) or (n_samples, n_outputs)

True labels for X.

sample_weightarray-like of shape (n_samples,), default=None

Sample weights.

Returns:

scorefloat

Mean accuracy of self.predict(X) wrt. y.

set_params(**params)

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as Pipeline). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters:

**paramsdict

Estimator parameters.

Returns:

selfestimator instance

Estimator instance.

transform(X)

Project data to maximize class separation.

Parameters:

Xarray-like of shape (n_samples, n_features)

Input data.

Returns:

X_newndarray of shape (n_samples, n_components) or (n_samples, min(rank, n_components))

Transformed data. In the case of the ‘svd’ solver, the shape is (n_samples, min(rank, n_components)).

Examples using sklearn.discriminant_analysis.LinearDiscriminantAnalysis

Linear and Quadratic Discriminant Analysis with covariance ellipsoid

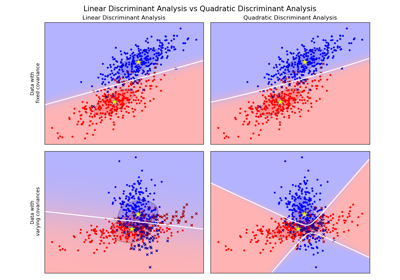
Linear and Quadratic Discriminant Analysis with covariance ellipsoid

Normal, Ledoit-Wolf and OAS Linear Discriminant Analysis for classification

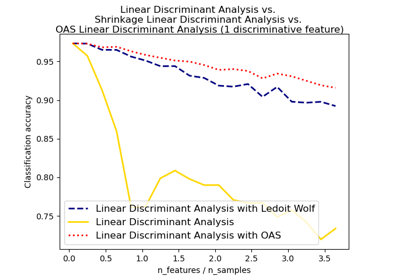
Normal, Ledoit-Wolf and OAS Linear Discriminant Analysis for classification

Comparison of LDA and PCA 2D projection of Iris dataset

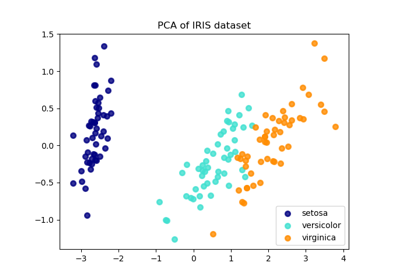
Comparison of LDA and PCA 2D projection of Iris dataset

Manifold learning on handwritten digits: Locally Linear Embedding, Isomap…

Manifold learning on handwritten digits: Locally Linear Embedding, Isomap...

Dimensionality Reduction with Neighborhood Components Analysis

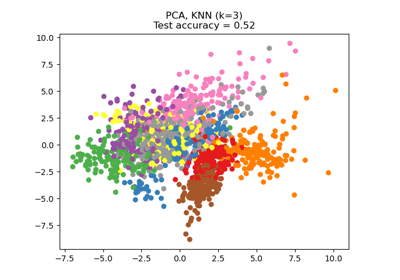
Dimensionality Reduction with Neighborhood Components Analysis